Слайд 2
1. Пояснительная записка
Тема «Квадратные уравнения» является важной
в курсе алгебры, так как создает базу для изучения
квадратичной функции, квадратных неравенств и алгебраических уравнений, сводящимся к квадратным, систем, изучаемым в дальнейшем.
В ходе изучения данной темы осуществляются межпредметные связи, формируются у учащихся система знаний об окружающем мире. Различные понятия физики-сведения о движении тела, брошенного вниз, о давлении жидкости и газа, составление и решение задач с техническим содержанием –необходимое условие реализации мировоззренческого потенциала курса алгебры.
Слайд 3
2. Цели и задачи раздела
Образовательные: Выработать умения решать квадратные уравнения и простейшие рациональные
уравнения и применять их к решению задач.
Воспитательные: Формировать логическое мышление, владение системой знаний о природе, обществе, человеке; добросовестное отношение к труду, организованность, дисциплинированность.
Развивающие: Развитие памяти учащихся, умений преодолевать трудности при решении математических задач, развитие любознательности.
Слайд 4
3. Психолого-педагогическое объяснение специфики восприятия и
освоения учебного материала учащимися.
У детей 14-15
летнего возраста происходит глубокая перестройка организма. Внимание детей избирательно, они откликаются на необычные уроки, быстрая переключаемость внимания не дает сосредотачиваться на одном и том же деле.
Значительной особенностью мышления детей является критичность. У детей появилось собственное мнение, которое они демонстрируют как можно чаще, заявляя о себе. Учащимся интересны уроки, в которых можно высказать собственное мнение, суждение.
Одной из самых главных моральных проблем детей является несогласованность убеждений , нравственных понятий с поступками, действиями , поведением. Система оценочных суждений, нравственных идеалов неустойчива. Моя работа, как учителя, направлена на формирование положительных качеств, развитие системы справедливых оценочных суждений.
Слайд 5
4. В результате изучения темы учащиеся должны уметь:
Решать
квадратные уравнения и дробные рациональные уравнения.
Решать текстовые задачи алгебраическим
методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для описания зависимостей между физическими величинами при исследовании несложных практических ситуаций.
Правильно употреблять и понимать термины:
квадратное уравнение, корни уравнения, решить уравнение
старший коэффициент, второй коэффициент, свободный член
полное квадратное уравнение, неполное квадратное уравнение
приведенное квадратное уравнение
дискриминант квадратного уравнения
рациональное уравнение, биквадратное уравнение
Слайд 6
5. Обоснование используемых образовательных технологий, методов , форм
организации деятельности учащихся
При закреплении изученного обеспечивается усвоение учащимися учебного
материала. Как известно, знания усваиваются только в ходе соответствующей собственной работы с ними. Поэтому особое внимание должно уделяться организации собственной деятельности учащихся в форме, позволяющей учителю проконтролировать ее ход и получаемые результаты.
Необходимо сочетать традиционные формы обучения с современными методами. Применение компьютерных технологий упрощает усвоение материала, вызывает интерес учащихся к предмету, развивает их кругозор.
Слайд 7
6. Система знаний
и система деятельности
Познавательная деятельность основана на внимании, восприятии
изучаемого материала, размышлении, анализе суждений, воображении.
Преобразующая деятельность: 1) учащийся выполняет конкретное задание, помогающее глубже понять данный материал; 2) это задание направляет усилия учащегося на использование определенного приема мыслительной деятельности; 3) учащийся обладает знаниями, необходимыми для выполнения этого задания, и навыками применения данного приема.
Общеучебная деятельность:
Навыки общения – слушать, уметь задавать вопросы и давать полные ответы.
Работа с литературой – научить ребенка пользоваться предметным указателем, оглавлением. Найти нужное правило.
Взаимообучение (работа в группе, работа в паре, взаимопроверка).
Самоорганизующая деятельность: (выработка правильной самооценки)
Слайд 8
7. Поурочное планирование темы
«Квадратные уравнения»
21 час
Слайд 9
«РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ»
Урок по
теме
Тип урока: урок обобщения и систематизации знаний, 8 класс
Цели
урока:
Образовательные: закрепить умение решать различные квадратные уравнения; повторить теорему Виета и теорему, обратную теореме Виета, выявить степень готовности учащихся к контрольной работе.
Воспитательные: формирование логического мышления, развитие таких качеств личности, как ответственность, дисциплинированность, самоконтроль, взаимовыручка.
Развивающие: развитие памяти учащихся, познавательного интереса, мышления, кругозора.
Слайд 10
Оборудование и материалы
к уроку
Оборудование: учебник «Алгебра 8» Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.
Суворов – М.: Просвещение, 2010; записи на доске; плакаты; карточки для индивидуальной самостоятельной работы, презентация к уроку.
Слайд 13
Квадратным уравнением называется уравнение ах2 + вх +
с = 0,
где а, в , с –
некоторые числа,
а ≠0, х- неизвестное
Какое уравнение называется квадратным?
Слайд 14
КВАДРАТНЫЕ УРАВНЕНИЯ
ПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ
НЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ
а ≠ 0,
в ≠ 0, с ≠ 0
а ≠ 0,
в = 0, с = 0
2х2+5х-7=0
6х+х2-3=0
х2-8х-7=0
25-10х+х2=0
3х2-2х=0
2х+х2=0
125+5х2=0
49х2-81=0
Слайд 15
Решите неполные квадратные уравнения:
5х² = 0;
2х² – 18 = 0;
4х ²
+ 16 = 0;
х ² – 6х = 0;
3х ² = х.
Слайд 16
Как определить число корней квадратного уравнения, не решая
его?
D = b2 - 4ac
D=0
1корень
D0
2корня
решая уравнения, определить ,
сколько корней оно имеет:
2х² – х + 3 = 0;
х ² – 3х – 5 = 0;
9х ² – 12х + 4 = 0.
D=1-4*6=-23
D=9-4*(-5)=29
D=144-4*36=0
Слайд 18
Какое квадратное уравнение называется
приведенным?
Квадратное уравнение вида
х² + рх + q = 0
называется приведенным
Слайд 19
В 1591 ввёл буквенные обозначения не только для
неизвестных величин, но и для коэффициентов уравнений; благодаря этому
стало впервые возможным выражение свойств уравнений и их корней общими формулами. Ему принадлежит установление единообразного приёма решения уравнений 2-й, 3-й и 4-й степеней.
В 1591 г доказал знаменитую теорему о корнях квадратного уравнения
Франсуа Виет
1540 -1603
Слайд 20
Если действительные числа x 1 и x 2
таковы, что x 1 + x 2= –
p
и x 1x 2= q,
то эти числа являются корнями квадратного уравнения
x ² + px + q = 0.
Теорема, обратная
теореме Виета
Теорема Виета
Сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Слайд 21
Х2 – 14Х + 24 = 0
D=b2 –
4ac = 196 – 96 = 100
X1
= 2, X2 = 12
X1 + X2 = 14, X1•X2 = 24
Повторим
Слайд 24
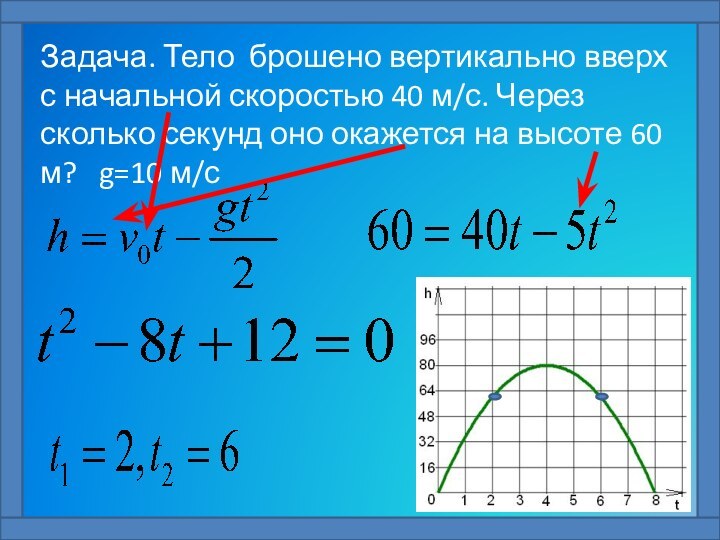
Задача. Тело брошено вертикально вверх с начальной скоростью
40 м/с. Через сколько секунд оно окажется на высоте
60 м? g=10 м/с
Слайд 26
Самостоятельная работа. Приложения.
ВАРИАНТ 1
1. Решите уравнение 0,5x2
- 2 = 0
а) 2; -2
б) нет корней в) 2
2 Решите уравнение 4x2 - 8x = 0
а) Нет корней б) 0; 2 в) 0; -2
3. Определите знаки корней, не решая уравнения: 4x2 - 11x + 7 = 0
а) оба положительны б) разных знаков в) оба отрицательны
4. Решите уравнение 3x2 + 5x - 2 = 0
а) -2; -6; б) - 2 ; 3 ; в) -2; 1/3
5. Какое из квадратных уравнений является приведённым:
а) 2х2 + 4х -7= 0 б) 8х -х2 + 4 = 0 в) х2 +5х – 6 = 0
Найдите корни уравнения, воспользовавшись теоремой Виета:
x2 - x - 6 = 0
а) -2; 3 б) -3; 2 в) 2; 3
Слайд 27
ВАРИАНТ 2
1. Решите уравнение 0,1x2 + 2,5
= 0
а) 2; -2
б) нет корней в) 2
2 Решите уравнение 5x2 + 15x = 0
а) Нет корней б) 0; 3 в) 0; -3
3. Определите знаки корней, не решая уравнения: 2x2 + 10x + 7 = 0
а) оба положительны б) разных знаков в) оба отрицательны
4. Решите уравнение 3x2 - 5x + 2 = 0
а) -1; -2/3 б) 2; 1/3 в) 1; 2/3
5. Какое из квадратных уравнений является приведённым:
а) 4х - х2 + 7= 0 б) 2х + х2 + 4 = 0 в) 7 х2 + х – 6 = 0
6. Найдите корни уравнения, воспользовавшись теоремой Виета: х2 + 8 x + 15 = 0
а) -5; - 3 б) 3; 5 в) 5; -3
Слайд 28
ВАРИАНТ 3
1. Решите уравнение 2x2 - 18
= 0
а) 3
б) нет корней в) 3; -3
2 Решите уравнение 6x2 - 18x = 0
а) Нет корней б) 0; 3 в) 0; -3
3. Определите знаки корней, не решая уравнения: 2x2 - 12x + 10 = 0
а) оба положительны б) разных знаков в) оба отрицательны
4. Решите уравнение -3x2 + 5x - 2 = 0
а) -2; -1/3 б) 2/3; 1 в) 2; 3
5. Какое из квадратных уравнений является приведённым:
а) 2х2 + 8х -7= 0 б) 2х - х2 +4 = 0 в) 5х + х2 – 6 = 0
6. Найдите корни уравнения, воспользовавшись теоремой Виета: x2 - 8x - 9 = 0
а) 9; -1 б) 1; -9 в) -1; -9
Слайд 29
ВАРИАНТ 4
1. Решите уравнение 3x2 + 27
= 0
а) 3; -3
б) 3 в) нет корней
2 Решите уравнение 3x2 + 24x = 0
а) Нет корней б) 0; 8 в) 0; -8
3. Определите знаки корней, не решая уравнения: 3x2 - 9x + 6 = 0
а) оба положительны б) разных знаков в) оба отрицательны
4. Решите уравнение 5x2 + 3x - 2 = 0
а) -1; -0,4 б) -1; 0,4 в) 1; 0,4
5. Какое из квадратных уравнений является приведённым:
а) 3х + х2 + 7= 0 б) -х2 + 6х + 4 = 0 в) 2х2 +5х – 6 = 0
Найдите корни уравнения, воспользовавшись теоремой Виета:
x2 - 3x - 10 = 0
а) -2; -5 б) 5; -2 в) 2; -5
Слайд 31
Приложение . Программированный контроль
ОТВЕТЫ: 1 вариант –
4, 3, 1, 2, 3, 1; 2 вариант –
1, 4, 2, 1, 2, 3
Домашнее задание
№654(б, г, е), №664, №583(б,
в)
Итог урока
Слайд 33
Контрольная работа №5 «Квадратные уравнения»
Слайд 35
Программы образовательных учреждений. Алгебра 7-9 классы. Составитель Бурмистрова
Т. А. – М. : Просвещение, 2008. авт.Ю.Н. Макарычев,
Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова
Конструирование современного урока математики. С.Г. Манвелов М.: Просвещение, 2005
Уроки математики с применением информационных технологий. 5-10 классы. Методическое пособие с электронным приложением / Л. Г. Горохова и др. – М: Издательство «Глобус»,2009. – (Современная школа).
Т.Д. Гончарова « Обучение на основе технологии полного усвоения» М.: Дрофа 2004
Учебник Алгебра 8 Ю.Н. Макарычев, Н.Г. Миндюк, К.И.Нешков М.: Просвещение ,2010
Дидактические материалы Алгебра 8, В.И.Жохов, Ю.Н.Макарычев, Н.Г. Миндюк М.: Просвещение, 2008
Список литературы