алгебраически замкнутым полем(т.е. многочлены с действительными коэффициентами могут не
иметь действительных корней).Пример:
Х2+1=0
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть








0
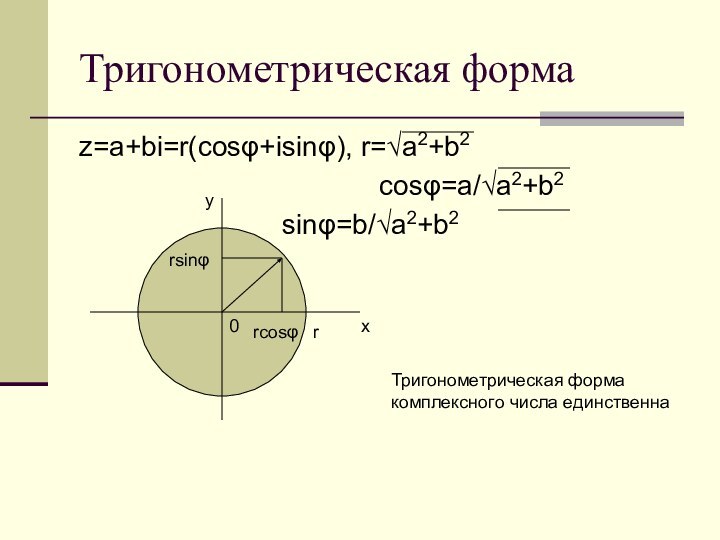
x
y
r
rcosφ
rsinφ
Тригонометрическая форма комплексного числа единственна