Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Взаимное расположение прямой и плоскости.Признак параллельностипрямой и плоскости.

Содержание

Взаимное расположение прямой и плоскости.αаαаАαа
Взаимное расположение прямой и плоскости. Признак параллельности прямой и плоскости.МОУ СОШ №256г.Фокино.2007 г. Взаимное расположение прямой и плоскости.αаαаАαа Построение прямой, не пересекающей плоскость.α1. Проведем плоскость α.2. В данной плоскости Построение прямой, не пересекающей плоскость.αа1АβаДоказательство:1) Пусть а ∩ α = B.В2) β Определение параллельности прямой и плоскости.Прямая и плоскость называются параллельными, если онине пересекаются.αаа Взаимное расположение прямой и плоскости.αаαаАαаа || α Построение параллельных прямой и плоскости.а1аαа || а1а || αПризнак параллельности прямой и На модели куба укажите плоскости, параллельные прямой DC, прямой DD1. Как установить На модели куба укажите плоскости, параллельные прямой DC, прямой DD1. Как установить Утверждение 1.Если плоскость проходит через данную прямую, параллельную другой плоскости, то линия Утверждение 2.Если одна из двух параллельных прямых параллельна данной плоскости, то другая Задача №18 (б)С1В1СВАαДоказать, что точки А, В1, С1 лежат на одной Домашнее задание:П. 6; №№ 18(а); 26; 28. Задача. Задача.
Слайды презентации

Слайд 2 Взаимное расположение прямой и плоскости.



α
а
α


а
А
α

а

Взаимное расположение прямой и плоскости.αаαаАαа

Слайд 3 Построение прямой, не пересекающей плоскость.

α
1. Проведем плоскость α.
2.

Построение прямой, не пересекающей плоскость.α1. Проведем плоскость α.2. В данной плоскости

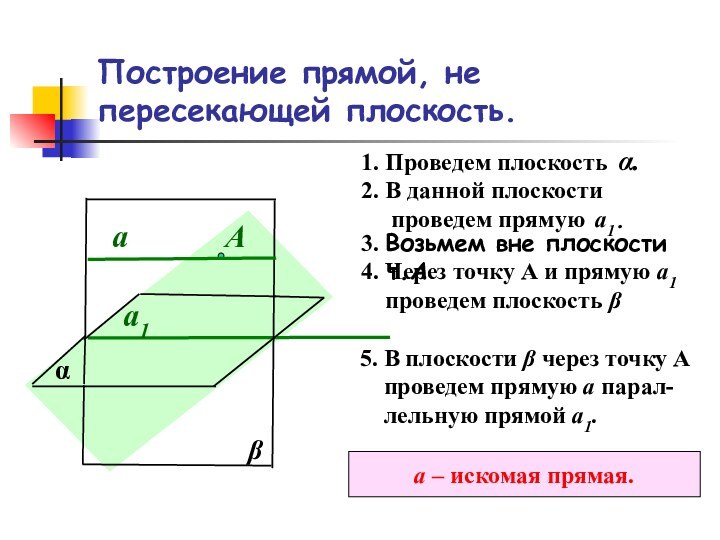
В данной плоскости
проведем прямую а1.

а1
3.

Возьмем вне плоскости т.А


А

4. Через точку А и прямую а1
проведем плоскость β













β

5. В плоскости β через точку А
проведем прямую а парал-
лельную прямой а1.


а

а – искомая прямая.

Слайд 4 Построение прямой, не пересекающей плоскость.

α

а1

А












β

а
Доказательство:
1) Пусть а ∩

Построение прямой, не пересекающей плоскость.αа1АβаДоказательство:1) Пусть а ∩ α = B.В2)

α = B.


В
2) β ∩ α = а1

В € β
В € α

В € а1, т.е.
а ∩ а1=В, что
противоречит
построению
( а || а1 )

а и α не пересекаются.

ч.т.д.

Слайд 5 Определение параллельности прямой и плоскости.
Прямая и плоскость называются

Определение параллельности прямой и плоскости.Прямая и плоскость называются параллельными, если онине


параллельными, если они
не пересекаются.

α
а
а || α или α ||

а

Слайд 6 Взаимное расположение прямой и плоскости.



α
а
α


а
А
α

а
а || α

Взаимное расположение прямой и плоскости.αаαаАαаа || α

Слайд 7 Построение параллельных прямой и плоскости.



а1
а
α

а || а1


а ||

Построение параллельных прямой и плоскости.а1аαа || а1а || αПризнак параллельности прямой

α
Признак параллельности прямой и плоскости.
Если прямая, не лежащая в

данной
плоскости, параллельна какой-нибудь
прямой в этой плоскости, то она
параллельна и самой плоскости.

Слайд 8 На модели куба укажите плоскости, параллельные прямой DC,

На модели куба укажите плоскости, параллельные прямой DC, прямой DD1. Как

прямой DD1. Как установить параллельность прямой и плоскости?
C1
C






DC || (AA1B1)
DC

|| (A1B1C1)

Слайд 9 На модели куба укажите плоскости, параллельные прямой DC,

На модели куба укажите плоскости, параллельные прямой DC, прямой DD1. Как

прямой DD1. Как установить параллельность прямой и плоскости?
C1
C










DD1 || (AA1B1)
DD1

|| (B1C1C)

Слайд 10 Утверждение 1.
Если плоскость проходит через данную прямую, параллельную

Утверждение 1.Если плоскость проходит через данную прямую, параллельную другой плоскости, то

другой плоскости, то линия пересечения плоскостей параллельна данной прямой.

α













β

а
b

Слайд 11 Утверждение 2.
Если одна из двух параллельных прямых параллельна

Утверждение 2.Если одна из двух параллельных прямых параллельна данной плоскости, то

данной плоскости, то другая прямая либо также параллельна этой

плоскости, либо лежит в этой плоскости.


а

b

с

Слайд 12 Задача №18 (б)



С1
В1
С
В
А




α
Доказать, что точки А, В1, С1

Задача №18 (б)С1В1СВАαДоказать, что точки А, В1, С1 лежат на одной

лежат на
одной прямой.
Дано: С € АВ; А

€ α;ВВ1 || СС1
ВВ1 ∩ α = В1; В1 € α;
СС1 ∩ α = С1; С1 € α;
АС : СВ = 3 : 2;
ВВ1 = 20 см.
Найти: СС1

2. Найти СС1 используя подобие треугольников.

12 см.

3

2

Слайд 13 Домашнее задание:
П. 6; №№ 18(а); 26; 28.

Домашнее задание:П. 6; №№ 18(а); 26; 28.

Слайд 14 Задача.

Задача.
  • Имя файла: vzaimnoe-raspolozhenie-pryamoy-i-ploskostipriznak-parallelnostipryamoy-i-ploskosti.pptx
  • Количество просмотров: 120
  • Количество скачиваний: 0
- Предыдущая Відрізок і його довжина
Следующая - Босова. Информатика

Похожие презентации

Этапы проведения измерений Этапы проведения измерений 133
Учебно-методический комплект урока по математике Дополнение до круглого десятка 2 класс план-конспект урока по математике (2 класс) по теме Учебно-методический комплект урока по математике Дополнение до круглого десятка 2 класс план-конспект урока по математике (2 класс) по теме 119
презентация Нахождение нескольких долей числа УМК Начальная школа XXI века презентация к уроку по математике (2 класс) презентация Нахождение нескольких долей числа УМК Начальная школа XXI века презентация к уроку по математике (2 класс) 135
Библиотечный урок по теме: Мастер и Маргарита. Библиотечный урок по теме: Мастер и Маргарита. 100
НОД в подготовительной группе по формированию элементарных математических представлений Тема: Площадь. учебно-методический материал по математике (подготовительная группа) НОД в подготовительной группе по формированию элементарных математических представлений Тема: Площадь. учебно-методический материал по математике (подготовительная группа) 125
Прямоугольный треугольник и его свойства Прямоугольный треугольник и его свойства 88
Правильные и полуправильные многогранники Правильные и полуправильные многогранники 95
Презентация к уроку математики по теме Урок закрепления презентация к уроку по математике (4 класс) Презентация к уроку математики по теме Урок закрепления презентация к уроку по математике (4 класс) 47
prezentatsiya 3 prezentatsiya 3 164
Презентация к уроку математики в 5 классе на тему: Десятичная система записи натуральных чисел Презентация к уроку математики в 5 классе на тему: Десятичная система записи натуральных чисел 163
Аттестационная работа. Золотое сечение. Математический язык красоты Аттестационная работа. Золотое сечение. Математический язык красоты 115
Урок математики 4 класс Тема: Письменное деление на числа, оканчивающиеся нулями методическая разработка по математике (4 класс) по теме Урок математики 4 класс Тема: Письменное деление на числа, оканчивающиеся нулями методическая разработка по математике (4 класс) по теме 127
diagramma diagramma 146
Математика 1 класс презентация к уроку (математика, 1 класс) по теме Математика 1 класс презентация к уроку (математика, 1 класс) по теме 121
Решение задач с помощью систем уравнений Решение задач с помощью систем уравнений 105
Презентация по математике на тему Объём тела Презентация по математике на тему Объём тела 117
Презентация Знакомство с задачей 1 класс презентация к уроку по математике (1 класс) Презентация Знакомство с задачей 1 класс презентация к уроку по математике (1 класс) 46
Аліквотні дроби Аліквотні дроби 112
Равные множества. (1 класс) Равные множества. (1 класс) 122
Презентация по математике 1 класс. Решение задач. презентация к уроку по математике (1 класс) по теме Презентация по математике 1 класс. Решение задач. презентация к уроку по математике (1 класс) по теме 112
Расстояние от точки до плоскости Расстояние от точки до плоскости 110
Нахождение наибольшего и наименьшего значения функции Нахождение наибольшего и наименьшего значения функции 103
Путешествие в город Математинск Путешествие в город Математинск 161
Семинар для родителей Играем с Блоками Дьенеша презентация по математике по теме Семинар для родителей Играем с Блоками Дьенеша презентация по математике по теме 431
пересечение поверхности пересечение поверхности 106
Как возникли дроби Как возникли дроби 116
Презентация урока-сказки Решение задач презентация урока для интерактивной доски по математике (3 класс) по теме Презентация урока-сказки Решение задач презентация урока для интерактивной доски по математике (3 класс) по теме 115
Сказочные герои в задачах по математике Сказочные герои в задачах по математике 154
Конспект занятия Незнайка в стране математики план-конспект занятия по математике (средняя группа) Конспект занятия Незнайка в стране математики план-конспект занятия по математике (средняя группа) 57
Раскрась флажки игра-тренажёр по математике 2 класс по теме Уравнение презентация к уроку по математике (2 класс) Раскрась флажки игра-тренажёр по математике 2 класс по теме Уравнение презентация к уроку по математике (2 класс) 41