- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Методические особенности обучения учащихся решению уравнений в курсе математики 5-7 классов
Содержание
- 2. Уравнение – это золотой ключ,
- 3. Цели: рассмотреть различные виды уравнений, изучаемые
- 4. Алгоритм – понятное предписание, указывающее, какие операции
- 5. Характеристические свойства понятия «алгоритм»: Свойство массовости Свойство дискретности и элементарности шагов Свойство результативности Свойство детерминированности
- 6. Всякий алгоритм описывает общий метод решения класса однотипных задач
- 7. Правило - «свернутый» алгоритм
- 8. Всякий алгоритм можно назвать правилом, но не всякое правило можно назвать алгоритмом
- 9. Три основных этапа: введение алгоритма; усвоение алгоритма; применение алгоритма.
- 10. Цели этапов:цель первого этапа – актуализация знаний,
- 11. Формы работы с учащимися: на первом этапе
- 12. V класс Уравнения решаются на основе зависимости между результатом и компонентами арифметического действия.
- 13. a+x=b Правило: «Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое».
- 14. a – x = в x –
- 15. V класс13899 + x = 2716 +
- 16. V класс1) x + 37 = 85;2)
- 17. V классПравило 1: Чтобы найти неизвестное слагаемое,
- 18. Учащиеся V класса сначала должны определить неизвестный
- 19. Задания:1. Заполните пропуски в формулировках и определениях.Уравнением
- 20. Задания:2. Заполните пустые клетки в таблице.
- 21. 3. Узнайте, какое слово зашифровано в таблице.
- 22. VI классОбщий приём решения уравнений: слагаемое можно
- 23. VI класс–x = 607-а = -30,04-5 +
- 24. «Универсальный» алгоритм решения линейных уравнений с одним
- 25. Пример5х + 3 = 2х + 9
- 26. Первый этап формирования алгоритма Устные упражнения на
- 27. Первый этап формирования алгоритма Устные упражнения на
- 28. Первый вид тестовых заданий 1. Если перед
- 29. Первый вид тестовых заданий 4. Коэффициентом такого
- 30. Второй вид тестовых заданий1. Выражение a +
- 31. Третий вид тестовых заданий 1. Раскройте скобки
- 32. Второй этап формирования алгоритмаРешите уравнения:1) -2x +
- 33. Третий этап формирования алгоритмаРешите уравнения:18 = 3y
- 34. Тестовые задания1. Решите уравнение: 4,2х + 5
- 35. Тестовые задания3. Отец в два раза старше
- 36. Самостоятельная работа1. Решите уравнения:а) 2,1х – 3,5
- 37. VII класс0,5(4 – 2a) = a –
- 38. Алгоритм решения линейного уравнения с двумя переменными
- 39. Пример3x + 2y = 12 (1)2y =
- 40. Тестовые задания по теме: «Уравнение с
- 41. Тестовые задания по теме «Уравнения с
- 42. Самостоятельная работа1. Решите уравнения:а) -8х = -24;б)
- 43. Скачать презентацию
- 44. Похожие презентации
Уравнение – это золотой ключ, открывающий все математические сезамы. С. Коваль










































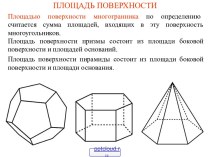
Слайд 3 Цели: рассмотреть различные виды уравнений, изучаемые в курсе
математики 5-7 классов; привести алгоритмы их решения; дать методические
рекомендации по обучению учащихся решению уравнений.Слайд 4 Алгоритм – понятное предписание, указывающее, какие операции и
в какой последовательности необходимо выполнить с данными, чтобы решить
любую задачу данного типа.
Слайд 5
Характеристические свойства понятия «алгоритм»:
Свойство массовости
Свойство дискретности
и элементарности шагов
Свойство результативности
Свойство детерминированности
Слайд 10
Цели этапов:
цель первого этапа – актуализация знаний, необходимых
для введения и обоснования алгоритма, а также формулирование алгоритма;
цель
второго этапа – отработка операций, входящих в алгоритм, и усвоение их последовательности;цель третьего этапа – отработка алгоритма в знакомых (при варьировании исходных данных) и незнакомых ситуациях.
Слайд 11
Формы работы с учащимися:
на первом этапе -
устная работа на повторение.
на втором этапе – письменная
коллективная работа с широким использованием комментирования выполняемых действий. на третьем этапе – самостоятельная работа.
Слайд 12
V класс
Уравнения решаются на основе зависимости между
результатом и компонентами арифметического действия.
Слайд 13
a+x=b
Правило:
«Чтобы найти неизвестное слагаемое, надо из
суммы вычесть известное слагаемое».
Слайд 14 a – x = в x – a =
в
1) «Чтобы найти неизвестное уменьшаемое, надо сложить вычитаемое и
разность»;2) «Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность».
Слайд 15
V класс
13899 + x = 2716 + 13899
4х
+ 4х = 424
15а – 8а = 714
8,6
– (x + 2,75) = 1,8545,7х + 0,3х – 2,4 = 89,6
x + 2,8 = 3,72 + 0,38
Слайд 16
V класс
1) x + 37 = 85;
2) m
– 94 = 18;
3) 85 – z = 36;
4)
4x = 144;5) x : 8 = 13;
6) 42 : x = 6
Слайд 17
V класс
Правило 1: Чтобы найти неизвестное слагаемое, надо
из суммы вычесть известное слагаемое.
Правило 2: Чтобы найти неизвестное
уменьшаемое, надо сложить вычитаемое и разность.Правило 3: Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Правило 4: Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
Правило 5: Чтобы найти неизвестное делимое, надо частное умножить на делитель.
Правило 6: Чтобы найти неизвестный делитель, надо делимое разделить на частное.
Слайд 18 Учащиеся V класса сначала должны определить неизвестный компонент
действия, а затем найти его, пользуясь одним из вышеперечисленных
правил.x + 25 = 50
x = 50 – 25
x = 25
Ответ: 25
y + 64 = 48 + 38
y + 64 = 86
y = 86 – 64
y = 22
Ответ: 22
Слайд 19
Задания:
1. Заполните пропуски в формулировках и определениях.
Уравнением называется
____________, содержащее ____________.
Корнем уравнения называется такое значение ______________, при
котором уравнение обращается в _____________ равенство.Чтобы найти неизвестное уменьшаемое, нужно к _____________ вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно _______________ вычесть _______________.
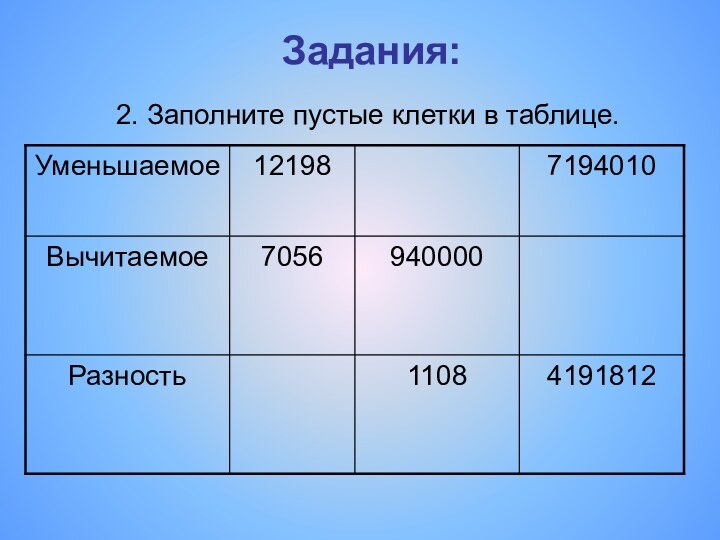
Слайд 22
VI класс
Общий приём решения уравнений:
слагаемое можно перенести
из одной части уравнения в другую, изменив при этом
его знак.
Слайд 23
VI класс
–x = 607
-а = -30,04
-5 + (а
- 25) = -4
|y| = 20
|a| = 0
|b| =
-37,2 – (6,2 - x) = 2,2
|x| = 9
Слайд 24 «Универсальный» алгоритм решения линейных уравнений с одним неизвестным
вида: 6x – 12 = 5x + 4
1)
раскрыть скобки (если таковые имеются);2) оставить неизвестные в одной части уравнения, известные – в другой (уединение неизвестных);
3) привести подобные слагаемые;
4) разделить обе части уравнения на коэффициент при неизвестном;
5) записать ответ.
Слайд 26
Первый этап формирования алгоритма
Устные упражнения на повторение:
1) Перенесите из левой части уравнения в правую то
слагаемое, которое не содержит неизвестного: а) 8х + 5,9 = 7х + 20;
б) 6х – 8 = -5х – 1,6.
2) Оставьте в левой части уравнения все слагаемые, содержащие неизвестное, а в правой – не содержащие неизвестное:
а) 15y – 8 = -6y +4,6;
б) -16z + 1,7 = 2z – 1.
Слайд 27
Первый этап формирования алгоритма
Устные упражнения на повторение:
3) Приведите подобные слагаемые:
а) 15t + 8 – 8t
– 6;б) 13a + 4 – 7a - 25a;
в) 24m + 7 – 9m – 14m.
4) Раскройте скобки и приведите подобные слагаемые:
а) 7b – (3b + 1);
б) 3(x - 5) + 10x;
в) -2(x + 1) + x.
Слайд 28
Первый вид тестовых заданий
1. Если перед скобками
стоит знак «+», то можно опустить скобки и этот
знак «+», _________________ знаки слагаемых, стоящих в скобках.2. Раскройте скобки:
-17,5 + (3,02 – 2,51) = __________________.
3. -(a + b) = __________________.
Слайд 29
Первый вид тестовых заданий
4. Коэффициентом такого выражения,
как a или ab, считают _________.
5. Слагаемые, имеющие одинаковую
буквенную часть, называют ______________________ слагаемыми.6. Выполните приведение подобных слагаемых:
b – 2c + 4b – c = _________________________.
7. Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то корни уравнения ________________________.
Слайд 30
Второй вид тестовых заданий
1. Выражение a + (b
+ c) можно записать без скобок:
a + (b +
c) = a + b + c2. Чтобы записать сумму, противоположную сумме нескольких слагаемых, надо изменить знаки данных слагаемых.
3. Приведение подобных слагаемых выполняют на основании переместительного свойства умножения.
4. Число -30 является корнем уравнения
0,5х – 15 = х.
Слайд 31
Третий вид тестовых заданий
1. Раскройте скобки в
выражении: a – (b + c - d)
А)
a – b + c – d;Б) a – b – c + d;
В) a + b + c – d.
2. Найдите значение выражения: 25 – (12 - 53)
А) -40;
Б) -16;
В) 66.
3. Упростите: 5x – 5y – 6x + y
А) –x – 5y;
Б) -6x + y;
В) –x – 4y.
4. Найдите корень уравнения: 4 – 3y = 7 - y
А) 1,5;
Б) -1;
В) -1,5.
Слайд 32
Второй этап формирования алгоритма
Решите уравнения:
1) -2x + 16
= 5x – 19
2) 4(3 – 2x) + 24
= 2(3 + 2x)3) 15 – 3(x - 8) = 3
4) 0,5(4 + x) – 0,4(x - 3) = 2,5
5) 0,4(x - 9) – 0,3(x + 2) = 0,7
Слайд 33
Третий этап формирования алгоритма
Решите уравнения:
18 = 3y +
3
6x + 10 = 5x + 15
-5n – 16
= 3n8 – 5n = 10 – 4n
9m – 8 = 6m + 7
Слайд 34
Тестовые задания
1. Решите уравнение: 4,2х + 5 =
-7,6
А) 4;
Б) -3;
В) -0,3;
Г) другой ответ.
2. Найдите сумму корней
уравнений х + 11,7 = 8,7 и (3х + 4,6) – 6,6 = 8,7 + 2,2
А) 4,3;
Б) -7,4;
В) 1,3;
Г) другой ответ.
Слайд 35
Тестовые задания
3. Отец в два раза старше сына
и на 25 лет старше дочери. Сколько лет дочери,
если всем вместе им 95 лет?А) 23;
Б) 24;
В) 48;
Г) другой ответ.
Слайд 36
Самостоятельная работа
1. Решите уравнения:
а) 2,1х – 3,5 =
1,4х;
б) 2(4 – 1,9х) = 0,8 – 0,2х.
2. На
верхней полке в 3 раза больше книг, чем на нижней. После того, как с верхней полки сняли 15 книг, а на нижнюю добавили 11 книг, книг на обеих полках стало поровну. Сколько книг было на каждой полке первоначально?3. Путь из города в село турист прошел со скоростью 4,8 км/ч. На обратном пути он увеличил скорость до 6 км/ч, что позволило ему пройти это расстояние на 1 час быстрее. Найдите расстояние от города до села.
Слайд 38 Алгоритм решения линейного уравнения с двумя переменными типа:
5y – 2x = 1
1) воспользовавшись свойствами уравнений,
выразить из данного уравнения одну переменную через другую;2) воспользовавшись свойствами уравнений, добиться того, чтобы коэффициент при одной из переменных был равен единице;
3) взять произвольное значение одной из переменных и вычислить соответствующее ему значение другой переменной;
4) записать решение исходного (данного) уравнения в виде пары (пар) чисел.
Слайд 39
Пример
3x + 2y = 12 (1)
2y = 12
– 3x
y = 6 – 1,5x (2)
если x
= 2, то = 6 – 3 = 3;если x = 6, то = 6 – 9 = -3.
Пары чисел (2; 3), (6;-3) – решение уравнения (1).
уравнение (1) имеет бесконечно много решений
Слайд 40
Тестовые задания по теме:
«Уравнение с одной переменной»
1.
Выберите уравнения, для которых число -3 является корнем:
1)
(2x + 3)(2x - 6) = 0; 3) (2x + 6)(x - 4) = 0;2) (x2 - 9) + (x2 - 7) = 2; 4) (x + 3)(x2 – 3x + 9) = 0.
а) 1; 2; б) всех; в) 3; 4; г) 2; 3; 4.
2. Найдите все натуральные значения p, при которых корнем уравнения px = 8 является целое число.
а) 1; 2; 4; 8; б) 1; 8; в) 2; 4; г) 2; 4; 8.
Слайд 41
Тестовые задания по теме
«Уравнения с двумя переменными»
1.
При каком значении c пара (c;3) является решением уравнения
3x
– 4y = 6?а) -6; б) 6.
2. Точка с абсциссой -3 принадлежит графику уравнения x – 2y = 10. Найдите ординату этой точки.
а) -6,5; б) 6,5; в) 4; г) -4.
Слайд 42
Самостоятельная работа
1. Решите уравнения:
а) -8х = -24;
б) 50х
= -5;
в) -18х = 1.
2. Определите значение x, при
котором значение выражения -3х равно:а) 0; б) 6; в) -12;
3. При каких значениях a уравнение ax = 8:
1) имеет корень, равный -4, 0;
2) не имеет корней;
3) имеет отрицательный корень?