Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Методы решения логарифмических уравнений 2

Содержание

Презентация по теме:
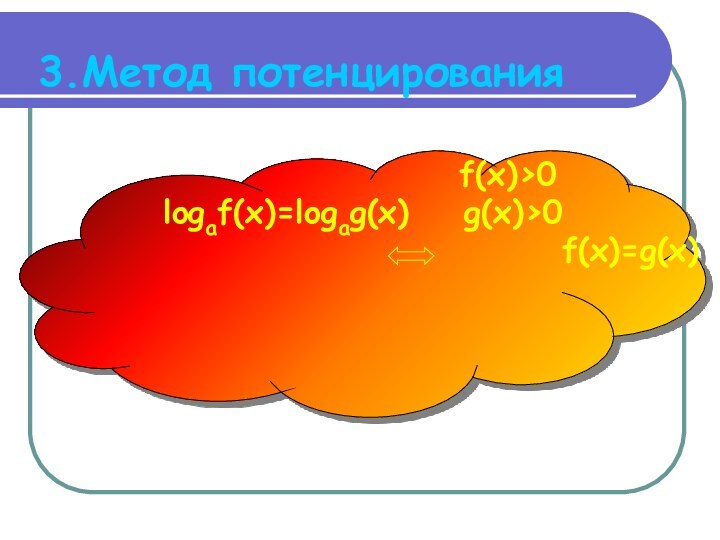
Работа выполнена: Ученицей 10 класса «б» МБОУСОШ №1 Презентация по теме: 1.Уравнения, решаемые по определению logab=c, ac =b, a>0, a≠1, b>0 Пример: log3(2-x)=2 ОДЗ: 2-x>02-x=32 x 2.Уравнения, решаемые с использованием основных свойств loga(bc) =loga│b│+loga│c│ loga(b/c)=loga│b│- loga│c│ Пример:log2(x+1)+log2(x+2)=1 ОДЗ: x+1>0 x>-1log2(x+1)(x+2)=1 3.Метод потенцирования Пример:lg(x-4)+lg(x-6)=lg8 ОДЗ: x-4>0 x>4 x>6lg(x-4)(x-6)=lg8 x-6>0 4.Метод подстановкиа)Уравнения, сводящиеся к квадратнымПример1:lg2x-3lgx+2=0 ОДЗ: Пример2:lg2(10x)=5-lgx ОДЗ: x>0(lg10+lgx)2=5-lgx1+2lgx+lg2x-5+lgx=0lg2x+3lgx-4=0пусть lgx=tt2+3t-4=0t1=1; t2= - 4если t1=1, б)Использование формулы logab=1/logba Пример:logx(9x2)log23x=4 ОДЗ: x>0 (logx9+logxx2)log23x=4 5.Метод приведения к одному основанию logab=logсb/logcaa>0,b>0, c>0 a≠1, c ≠1 Пример:log2x+log4x+log8x=11 ОДЗ:x>0log2x+log22x+log23x=11log2x+1/2log2x+1/3log2x=11,log2x ≠0,x ≠111/6log2x=11log2x=6x=26x=64Ответ: x=64 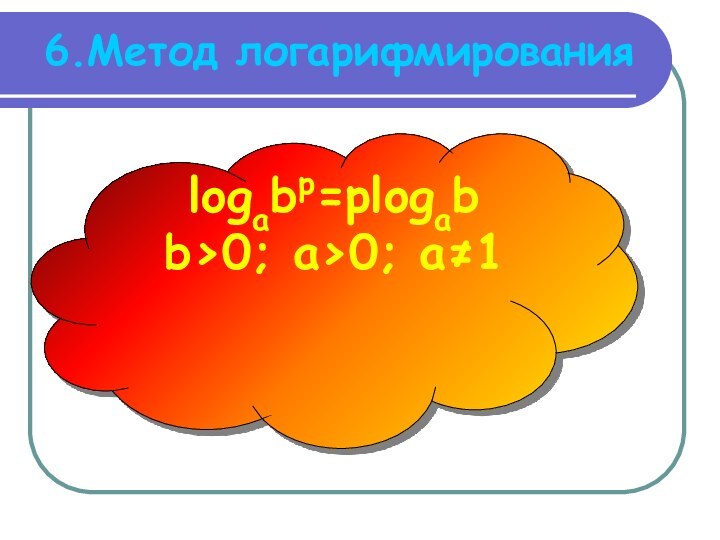6.Метод логарифмирования logabр=рlogabb>0; a>0; a≠1 Пример:x (lgx+5)/3 =105+lgx ОДЗ:x>0прологарифмируем уравнение по основанию 7.Использование специальной формулы a logсb = b logсab>0;b≠1 a>0; a≠1;с>0; с≠1 Пример:3xlog52+2log5x=64 ОДЗ: x>0,x ≠13*2log5x+2log5x=644*2log5x=64 |:42log5x=162log5x=24log5x=4x=54x=625Ответ: x=625 8.Использование свойств монотонности функцииПример:log3(x+1)+log4(5x+6)=3 ОДЗ: x> -1,2y= log3(x+1) - 9.Использование свойств ограниченности функцииПример:log2(17-|sin0,5πx|)=√2x+15-x2 , x ≥01)рассмотрим левую частьт.к. 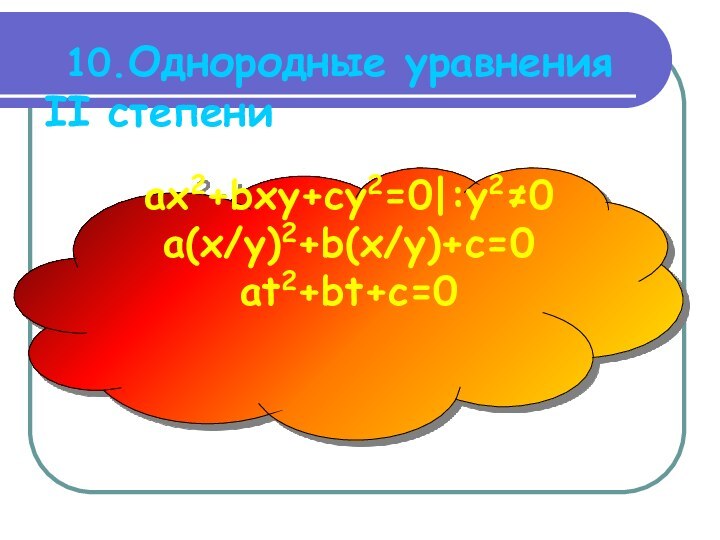0≤ |sin0,5πx| ≥ 10.Однородные уравнения II степени ax2+bxy+cy2=0|:y2≠0a(x/y)2+b(x/y)+c=0at2+bt+c=0 Пример:3log22(x+1)-4log2(2x+1)log2(x+1)+log22(2x+1)=0Делим на log22(2x+1) ОДЗ: x>1/2 3(log2(x+1)/log2(2x+1))2-4log2(2x+1)log2(x+1)/log22(2x+1)+1=0 11.Уравнения, содержащие неизвестное в основании и показатели степениПример:x√x=√xx 12.Функционально - графический метод(х – 1) = log2xСтроим графики функций у = Решить самостоятельноlq(х²-2х)=lg30-1;lg(x²+2x-3)=lg(6X-2);log3X*lоg2х =4 log32;log3X+log9X+log27X=1/12;log5(X-l0)-log5(X+2)=-1;3+ 2logX+13=2log3(X+1).
Слайды презентации

Слайд 2 Презентация по теме:

Презентация по теме:

Слайд 3 1.Уравнения, решаемые по определению

logab=c,
ac =b, a>0, a≠1,

1.Уравнения, решаемые по определению logab=c, ac =b, a>0, a≠1, b>0

Слайд 4 Пример:
log3(2-x)=2 ОДЗ: 2-x>0
2-x=32

Пример: log3(2-x)=2 ОДЗ: 2-x>02-x=32 x

x

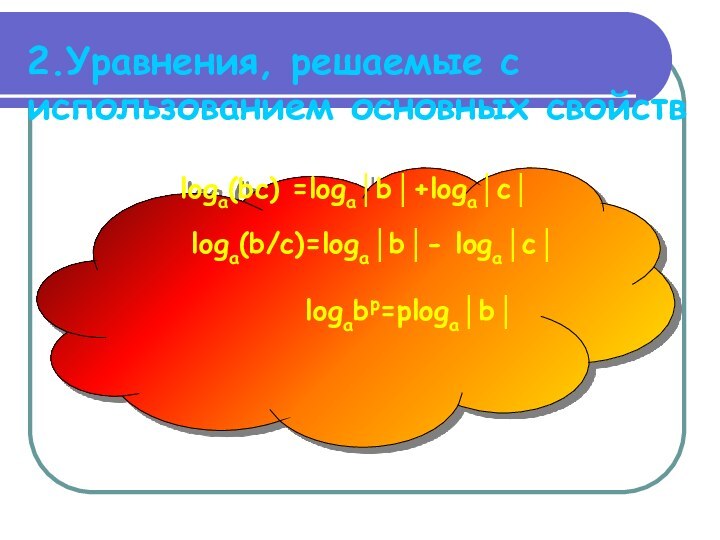
Слайд 5 2.Уравнения, решаемые с использованием основных свойств
loga(bc) =loga│b│+loga│c│

2.Уравнения, решаемые с использованием основных свойств loga(bc) =loga│b│+loga│c│ loga(b/c)=loga│b│- loga│c│

loga(b/c)=loga│b│- loga│c│

logabp=ploga│b│


Слайд 6 Пример:
log2(x+1)+log2(x+2)=1 ОДЗ: x+1>0 x>-1
log2(x+1)(x+2)=1

Пример:log2(x+1)+log2(x+2)=1 ОДЗ: x+1>0 x>-1log2(x+1)(x+2)=1 x+2>0 x>-2 (x+1)(x+2)=21

x+2>0 x>-2
(x+1)(x+2)=21

х>-1
x2+3x=0
x(x+3)=0
x1=0 x2=-3(не уд. ОДЗ)
Ответ: x=0

Слайд 7 3.Метод потенцирования

3.Метод потенцирования

f(x)>0
logaf(x)=logag(x) g(x)>0
f(x)=g(x)

Слайд 8 Пример:
lg(x-4)+lg(x-6)=lg8 ОДЗ: x-4>0 x>4 x>6
lg(x-4)(x-6)=lg8

Пример:lg(x-4)+lg(x-6)=lg8 ОДЗ: x-4>0 x>4 x>6lg(x-4)(x-6)=lg8 x-6>0 x>6(x-4)(x-6)=8x2-10x+16=0x1=8x2=2 (не уд. ОДЗ)Проверка: x=8 lg4+lg2=lg8Lg8=lg8Ответ. 8

x-6>0 x>6
(x-4)(x-6)=8
x2-10x+16=0
x1=8
x2=2 (не уд. ОДЗ)
Проверка: x=8 lg4+lg2=lg8
Lg8=lg8
Ответ.

8

Слайд 9 4.Метод подстановки
а)Уравнения, сводящиеся к квадратным
Пример1:
lg2x-3lgx+2=0

4.Метод подстановкиа)Уравнения, сводящиеся к квадратнымПример1:lg2x-3lgx+2=0 ОДЗ: x>0

ОДЗ: x>0


пусть lgx=t, tєR
t2-3t+2=0
t1=1 t2=2
если t1=1, то если t2=2, то
lgx=1 lgx=2
x=10 x=100
Ответ: x1=10, x2=100


Слайд 10 Пример2:
lg2(10x)=5-lgx ОДЗ: x>0
(lg10+lgx)2=5-lgx
1+2lgx+lg2x-5+lgx=0
lg2x+3lgx-4=0
пусть lgx=t
t2+3t-4=0
t1=1;

Пример2:lg2(10x)=5-lgx ОДЗ: x>0(lg10+lgx)2=5-lgx1+2lgx+lg2x-5+lgx=0lg2x+3lgx-4=0пусть lgx=tt2+3t-4=0t1=1; t2= - 4если t1=1, то

t2= - 4
если t1=1, то если t2=

- 4,то
lgx=1 lgx=-4
x=10 x=0,0001
Ответ: x1=10, x2=0,0001










Слайд 11 б)Использование формулы

logab=1/logba

б)Использование формулы logab=1/logba

Слайд 12 Пример:
logx(9x2)log23x=4 ОДЗ:

Пример:logx(9x2)log23x=4 ОДЗ: x>0 (logx9+logxx2)log23x=4

x>0
(logx9+logxx2)log23x=4

x≠1
(2logx3+2)log23x=4
(2/log3x+2)log23x=4
пусть log3x=t (2/t+2)t2=4
2t2+2t-4=0
t1=1; t2=-2
если t1=1, то если t2=-2, то
log3x=1; x1=3; log3x=-2. x2=1/9.
Ответ: x1=3, x2=1/9

Слайд 13 5.Метод приведения к одному основанию

logab=logсb/logca
a>0,b>0, c>0 a≠1, c

5.Метод приведения к одному основанию logab=logсb/logcaa>0,b>0, c>0 a≠1, c ≠1

≠1

Слайд 14 Пример:
log2x+log4x+log8x=11 ОДЗ:x>0
log2x+log22x+log23x=11
log2x+1/2log2x+1/3log2x=11,log2x ≠0,x ≠1
11/6log2x=11
log2x=6
x=26
x=64
Ответ: x=64




Пример:log2x+log4x+log8x=11 ОДЗ:x>0log2x+log22x+log23x=11log2x+1/2log2x+1/3log2x=11,log2x ≠0,x ≠111/6log2x=11log2x=6x=26x=64Ответ: x=64

Слайд 15 6.Метод логарифмирования

logabр=рlogab
b>0; a>0; a≠1

6.Метод логарифмирования logabр=рlogabb>0; a>0; a≠1

Слайд 16 Пример:
x (lgx+5)/3 =105+lgx

Пример:x (lgx+5)/3 =105+lgx ОДЗ:x>0прологарифмируем уравнение по основанию 10lgx(lgx+5)/3=lg105+lgx((lgx+5)/3)lgx=(5+lgx)lg101/3(lgx+5)lgx=5+lgx|*3(lgx+5)lgx=15+3lgxlg2x+5lgx=15+3lgxlg2x+2lgx-15=0пусть lgx=tt2+2t-15=0t1=-5;

ОДЗ:x>0
прологарифмируем уравнение по основанию 10
lgx(lgx+5)/3=lg105+lgx
((lgx+5)/3)lgx=(5+lgx)lg10
1/3(lgx+5)lgx=5+lgx|*3
(lgx+5)lgx=15+3lgx
lg2x+5lgx=15+3lgx
lg2x+2lgx-15=0
пусть lgx=t
t2+2t-15=0
t1=-5; t2=3
если t1=-5,

то lgx=-5 если t2=3, то lgx=3
x1=0,00001 x2=1000
Ответ: x1=0,00001, x2=1000

Слайд 17 7.Использование специальной формулы
a logсb = b logсa
b>0;b≠1

7.Использование специальной формулы a logсb = b logсab>0;b≠1 a>0; a≠1;с>0; с≠1

a>0; a≠1;
с>0; с≠1

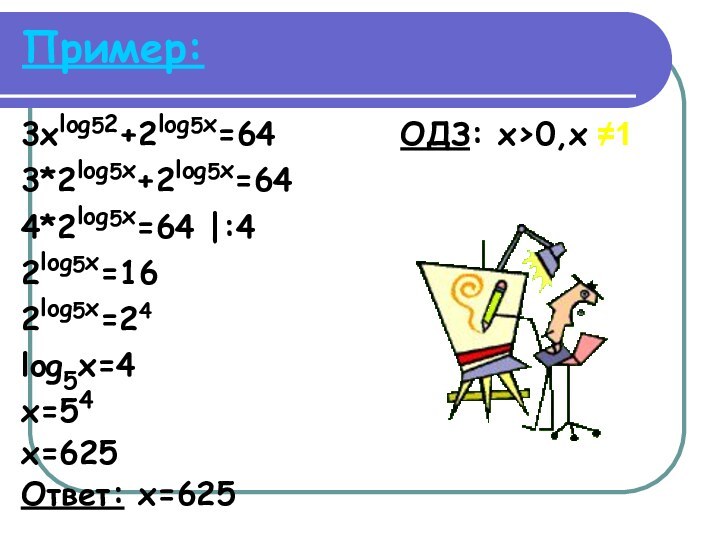
Слайд 18 Пример:
3xlog52+2log5x=64 ОДЗ: x>0,x ≠1
3*2log5x+2log5x=64
4*2log5x=64

Пример:3xlog52+2log5x=64 ОДЗ: x>0,x ≠13*2log5x+2log5x=644*2log5x=64 |:42log5x=162log5x=24log5x=4x=54x=625Ответ: x=625

|:4
2log5x=16
2log5x=24
log5x=4
x=54
x=625
Ответ: x=625

Слайд 19 8.Использование свойств монотонности функции
Пример:
log3(x+1)+log4(5x+6)=3 ОДЗ:

8.Использование свойств монотонности функцииПример:log3(x+1)+log4(5x+6)=3 ОДЗ: x> -1,2y= log3(x+1) - возрастающая

x> -1,2
y= log3(x+1) - возрастающая функция
y= log4(5x+6)- возрастающая функция
3

- const
Сумма двух возрастающих функций равна возрастающей функции.
Используем утверждение: если возр. функция
равна const или убыв. функции, тогда
уравнение имеет один корень, который находится с
помощью метода подбора.
Ответ: x=2

Слайд 20 9.Использование свойств ограниченности функции
Пример:
log2(17-|sin0,5πx|)=√2x+15-x2 , x ≥0
1)рассмотрим левую

9.Использование свойств ограниченности функцииПример:log2(17-|sin0,5πx|)=√2x+15-x2 , x ≥01)рассмотрим левую частьт.к. 0≤ |sin0,5πx|

часть
т.к. 0≤ |sin0,5πx| ≥ 1 ,то
log2(17-|sin0,5πx|) ≥log2(17-1)=log216=4 т.е.
0≤ |sin0,5πx|

≥ 4
при x=1 - достигается равенство
2)рассмотрим правую часть
√2x+15-x2= √16-(x+1) ≤ √16=4=16-(x-1)2
√2x+15-x2≤4
при x=1 – достигается равенство
Ответ: x=1

Слайд 21 10.Однородные уравнения II степени
ax2+bxy+cy2=0|:y2≠0
a(x/y)2+b(x/y)+c=0
at2+bt+c=0

10.Однородные уравнения II степени ax2+bxy+cy2=0|:y2≠0a(x/y)2+b(x/y)+c=0at2+bt+c=0

Слайд 22 Пример:
3log22(x+1)-4log2(2x+1)log2(x+1)+log22(2x+1)=0
Делим на log22(2x+1)

Пример:3log22(x+1)-4log2(2x+1)log2(x+1)+log22(2x+1)=0Делим на log22(2x+1) ОДЗ: x>1/2 3(log2(x+1)/log2(2x+1))2-4log2(2x+1)log2(x+1)/log22(2x+1)+1=0

ОДЗ: x>1/2
3(log2(x+1)/log2(2x+1))2-4log2(2x+1)log2(x+1)/log22(2x+1)+1=0

t
3t2-4t+1=0
t1=1 t2=1/3
если t1=1 то, если t2=1/3 то,
log2(x+1)/log2(2x+1)=1 log2(x+1)/log2(2x+1)=1/3
log2(x+1)=log2(2x+1) 3log2(x+1)=log2(2x+1)
x+1=2x+1 log2(x+1)3=2x+1
x=0 x(x2+3x+1)=0
x1=0 x2=(-3+√5)/2 x3=(-3-√5)/2
Ответ: x1=0, x2= =(-3+√5)/2 не уд.

Слайд 23 11.Уравнения, содержащие неизвестное в основании и показатели степени
Пример:
x√x=√xx

11.Уравнения, содержащие неизвестное в основании и показатели степениПример:x√x=√xx

ОДЗ: x>0,
logx x√x =logx √xx x≠ 1
logx xx0,5 =logx (x0,5)x
√xlogx x=0,5logxx
√x=0,5x
√x(1-0,5√x)=0
√x=0 (не уд.ОДЗ) (1-0,5√x)=0
√x=2
x=4
Ответ: x=4

Слайд 24 12.Функционально - графический метод
(х – 1) = log2x
Строим

12.Функционально - графический метод(х – 1) = log2xСтроим графики функций у

графики функций у = (х – 1) и
у

= log2x.
Ответ: х = 1, х=2.

1

1

2

х

у

0

  • Имя файла: metody-resheniya-logarifmicheskih-uravneniy-2.pptx
  • Количество просмотров: 114
  • Количество скачиваний: 0
- Предыдущая Погода
Следующая - Знакомство с джазом

Похожие презентации

Тест Меры массы презентация к уроку по математике (3 класс) по теме Тест Меры массы презентация к уроку по математике (3 класс) по теме 132
Симметрические системы уравнений Симметрические системы уравнений 136
презентация к уроку математики 2 класс презентация к уроку по математике (2 класс) по теме презентация к уроку математики 2 класс презентация к уроку по математике (2 класс) по теме 123
Расстояния между прямыми Расстояния между прямыми 106
Hypothesis testing Hypothesis testing 120
Концепция математического образования в начальной школе статья по математике по теме Концепция математического образования в начальной школе статья по математике по теме 135
Дидактическая игра Чей шарик? на тему Сложение и вычитание многозначных чисел-2 Дидактическая игра Чей шарик? на тему Сложение и вычитание многозначных чисел-2 110
Использование мультимедийных игр-презентаций при обучении детей старшего дошкольного возраста счету методическая разработка по математике (старшая группа) Благодаря мультимедийным играм-презентациям удаётся сконцентрировать внимание и привлечь интерес даж Использование мультимедийных игр-презентаций при обучении детей старшего дошкольного возраста счету методическая разработка по математике (старшая группа) Благодаря мультимедийным играм-презентациям удаётся сконцентрировать внимание и привлечь интерес даж 113
Презентация по теме Дроби Презентация по теме Дроби 170
Сложение и Вычитание в столбик 2 Класс Сложение и Вычитание в столбик 2 Класс 116
Презентация по математике на тему Уравнение ( 2 класс) Презентация по математике на тему Уравнение ( 2 класс) 136
Урок математики 3 класс Решение уравнений изученных видов. план-конспект урока по математике (3 класс) по теме Урок математики 3 класс Решение уравнений изученных видов. план-конспект урока по математике (3 класс) по теме 135
Учебно-методический комплект по математикеСпособ сложения столбиком с переходом через разряд учебно-методический материал по математике (2 класс) Учебно-методический комплект по математикеСпособ сложения столбиком с переходом через разряд учебно-методический материал по математике (2 класс) 132
Презентация Устный счёт. 2 класс презентация к уроку по математике (2 класс) Презентация Устный счёт. 2 класс презентация к уроку по математике (2 класс) 144
Учебно – методическое обеспечение образовательного процесса по учебному предмету Математика в 2017/2018 учебном году Учебно – методическое обеспечение образовательного процесса по учебному предмету Математика в 2017/2018 учебном году 99
Умножение и деление чисел на 10, 100 Умножение и деление чисел на 10, 100 105
технологическая карта, презентация урок математики 3 кл Тысяча. Счет сотнями презентация к уроку по математике (3 класс) по теме технологическая карта, презентация урок математики 3 кл Тысяча. Счет сотнями презентация к уроку по математике (3 класс) по теме 132
Презентація на тему Квадратична функція та її властивості (алгебра) Презентація на тему Квадратична функція та її властивості (алгебра) 187
ПрезентацияПрофессиональная деятельность и математика ПрезентацияПрофессиональная деятельность и математика 172
Египетские пирамиды Египетские пирамиды 104
arifmetika - kopiya arifmetika - kopiya 150
Деление и умножение чисел, оканчивающихся нулём Деление и умножение чисел, оканчивающихся нулём 121
Презентация к уроку математики Повторение . Признаки делимости (6 класс) Презентация к уроку математики Повторение . Признаки делимости (6 класс) 125
Вычисления с многозначными числами Вычисления с многозначными числами 119
Презентация Занятия удмуртов и скотоводство Презентация Занятия удмуртов и скотоводство 131
Формирование элементарных математических представлений у детей второй младшей группы посредством использования дидактических игр учебно-методический материал по математике (младшая группа) Формирование элементарных математических представлений у детей второй младшей группы посредством использования дидактических игр учебно-методический материал по математике (младшая группа) 114
Дроби в Вавилоне, Египте, Риме. Открытие десятичных дробей Дроби в Вавилоне, Египте, Риме. Открытие десятичных дробей 189
Урок математики в 4 классе Скорость сближения и скорость удаления Урок математики в 4 классе Скорость сближения и скорость удаления 99
Презентация к проекту Математика вокруг нас. Числа в загадках, пословицах, поговорках презентация к уроку по математике (1 класс) Презентация к проекту Математика вокруг нас. Числа в загадках, пословицах, поговорках презентация к уроку по математике (1 класс) 112
Алгебраические преобразования с параметрами Алгебраические преобразования с параметрами 127