- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Многогранники. Пирамиды
Содержание
- 2. Основные вопросы темы1.Определение2.Элементы3.Виды(подвиды)4.Общие сведения
- 3. 1.Определение- многоугольник АВСДЕ… лежит в плоскоститочка М не лежит в плоскостиМАВСДЕ…-пирамида
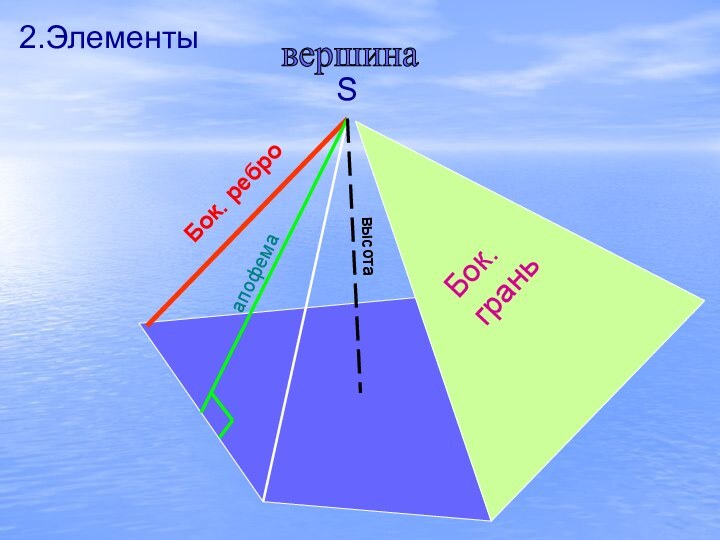
- 4. SвершинавысотаапофемаБок.грань2.ЭлементыБок. ребро
- 5. Площадь поверхностиSбок = S1 + S2 +
- 7. Обычные.Название пирамиды определяетсяпо названию многоугольника,лежащего в основании пирамиды.Например:
- 8. n=3Правильный тетраэдр.Все ребра равны.Не путать с правильной пирамидой!Треугольная пирамида
- 9. n=4Четырехугольная пирамидаПирамида Хеопсав Гизе (долина царей).
- 10. n=6Шестиугольная пирамида
- 11. Правильная пирамидаСвойстваФормулы1.Основание - правильный многоугольник2.Вершина проецируется в центр многоугольника
- 12. Свойства правильной пирамидыОснование - правильный многоугольник.2.Проекция вершины
- 13. ФормулыSбок=S1+S2+…+Sn==0,5 a1 * ha + 0,5 a2
- 14. 1212
- 15. oСвойства - бок. ребра равны- углы между
- 16. Свойства-все двугранные углы при основании равны -
- 17. 4.Общие сведенияИсторияСовременностьБиологическое воздействие
- 18. Исторические сведенияДолина царей «Красная» пирамида в ДашуреСтупенчатая пирамида ДжосераПирамида естественногопроисхождения
- 19. Геометрия Великой пирамидыПростые геометрические соотношения между элементами
- 20. Вот что на сегодняшний день известно о
- 21. Правильная четырехгранная пирамида является одной из хорошо
- 22. «Большой Лувр» послереставрации в 1981 г.Связь между
- 23. Французский ученый Жак Бержье, изучавший влияние различных
- 24. Задания1.Сколько граней, вершин, ребер у n-угольной пирамиды?2.Какое
- 25. Скачать презентацию
- 26. Похожие презентации



















Слайд 7
Обычные.
Название пирамиды определяется
по названию многоугольника,
лежащего в основании пирамиды.
Например:
Слайд 8
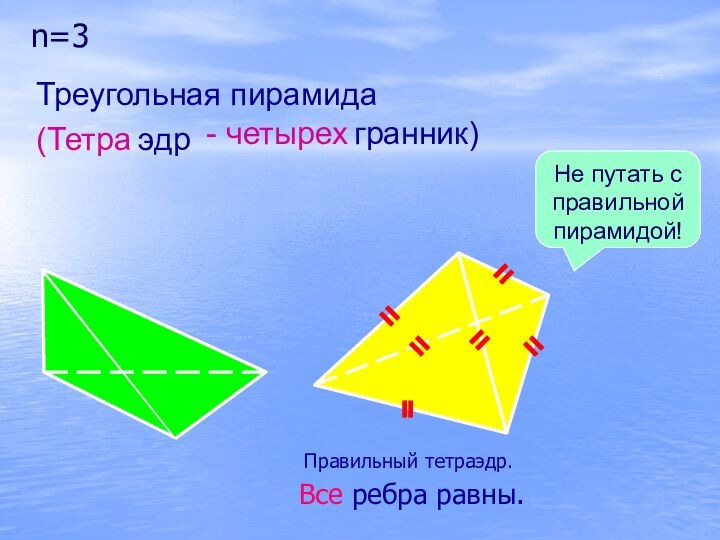
n=3
Правильный тетраэдр.
Все ребра равны.
Не путать с правильной
пирамидой!
Треугольная пирамида
Слайд 11
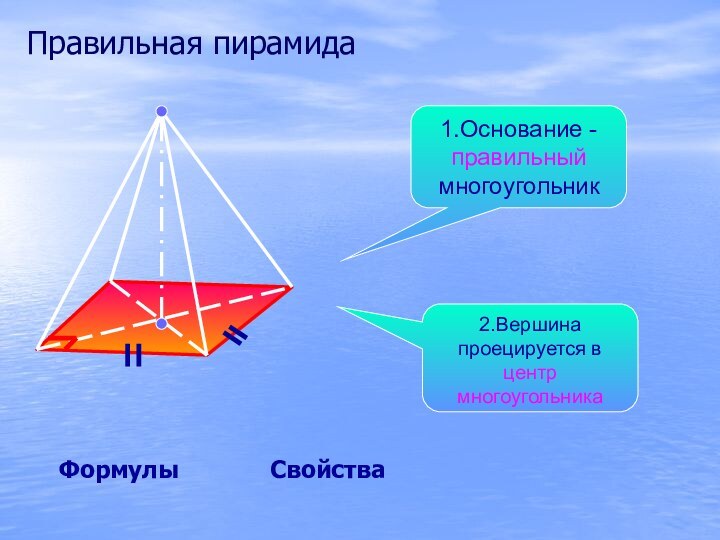
Правильная пирамида
Свойства
Формулы
1.Основание -
правильный многоугольник
2.Вершина проецируется в центр
многоугольника
Слайд 12
Свойства правильной пирамиды
Основание - правильный многоугольник.
2.Проекция вершины –
центр вписанной и
описанной окружностей.
3.Все боковые ребра равны.
4.Все боковые
ребра равнонаклонены к основанию.5.Все двугранные углы равны.
6.Все апофемы равны.
7.Все плоские углы при вершине равны.
Слайд 13
Формулы
Sбок=
S1+
S2+
…+
Sn=
=0,5 a1 * ha + 0,5 a2 *
ha +…+ 0,5 an * ha=
=0,5ha * (a1
+ a2 + … + an)=Периметр основания
= 0,5 ha * P осн.
Sбок =0,5 Росн.* ha
Слайд 15
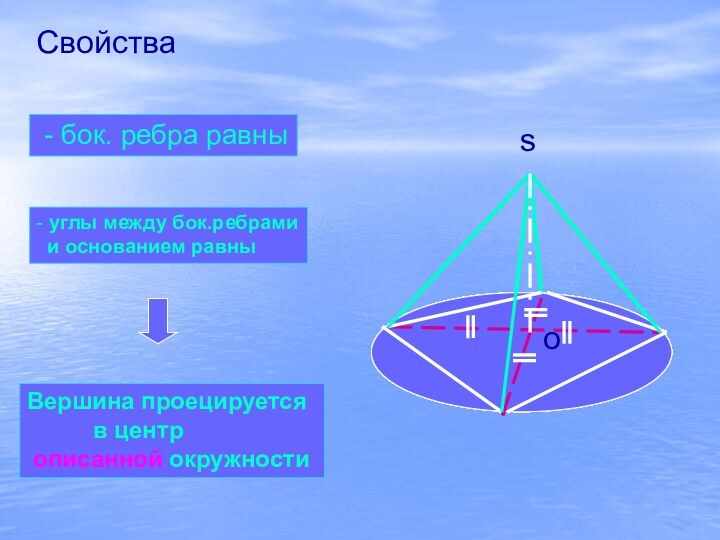
o
Свойства
- бок. ребра равны
- углы между бок.ребрами
и основанием равны
Вершина проецируется
в
центрописанной окружности
Слайд 16
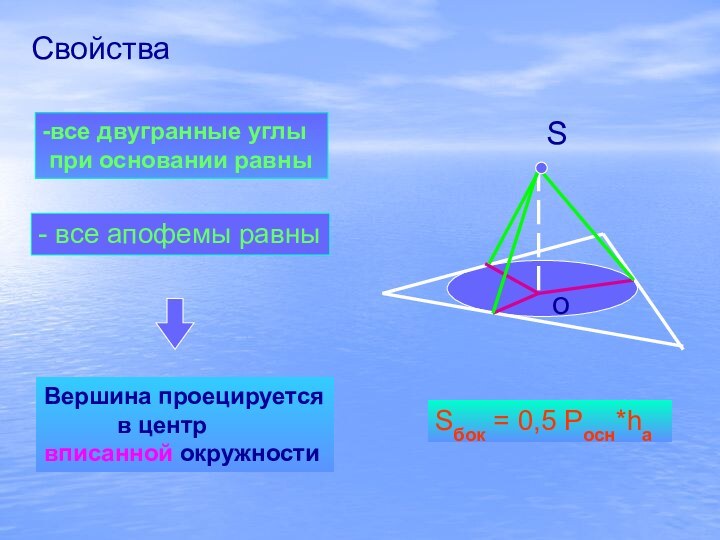
Свойства
-все двугранные углы
при основании равны
- все
апофемы равны
Вершина проецируется
в
центрвписанной окружности
S
o
Sбок = 0,5 Росн*ha
Слайд 18
Исторические сведения
Долина царей
«Красная» пирамида в Дашуре
Ступенчатая пирамида
Джосера
Пирамида естественного
происхождения
Слайд 19
Геометрия Великой пирамиды
Простые геометрические соотношения между элементами внутреннего
строения пирамиды Хеопса позволяют получить представление о первоначальном замысле
древних архитекторов.Слайд 20 Вот что на сегодняшний день известно о единственном
из сохранившихся семи чудес света - пирамиде Хеопса: построена
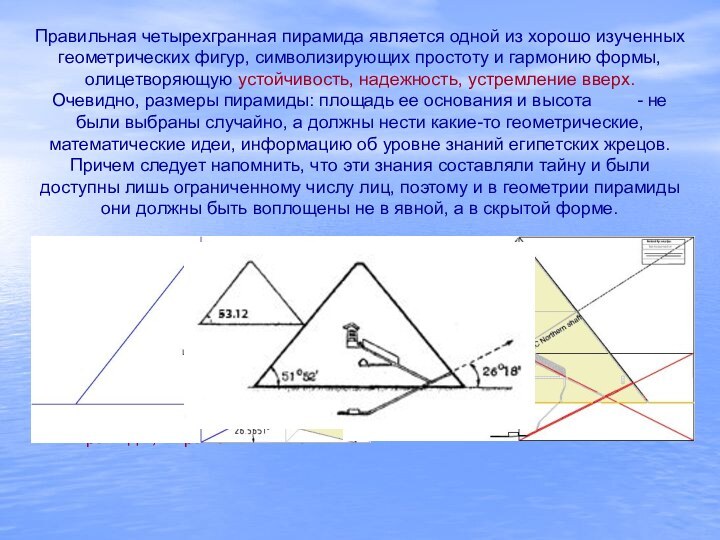
примерно 4500 лет назад во времена IV династии фараонов Древнего Египетского Царства, высота - 146.5 м (сейчас примерно 8 м верхушки отсутствует, как и внешняя облицовка), длина стороны - 230.5 м . Пирамида выложена из 2.5 миллионов блоков песчаника весом от 0.5 до 2 тонн .Слайд 21 Правильная четырехгранная пирамида является одной из хорошо изученных
геометрических фигур, символизирующих простоту и гармонию формы, олицетворяющую устойчивость,
надежность, устремление вверх.Очевидно, размеры пирамиды: площадь ее основания и высота - не были выбраны случайно, а должны нести какие-то геометрические, математические идеи, информацию об уровне знаний египетских жрецов. Причем следует напомнить, что эти знания составляли тайну и были доступны лишь ограниченному числу лиц, поэтому и в геометрии пирамиды они должны быть воплощены не в явной, а в скрытой форме.
Гениальные создатели пирамиды Хеопса стремились поразить далеких потомков глубиной своих знаний, и они достигли этого. Следует лишь удивляться высокому знанию и искусству древних математиков и архитекторов Египта, которые смогли воплотить в пирамиде две иррациональные (т.е. неизмеримые) величины – π и Ф со столь поразительной точностью, оперируя исходными отношениями целых чисел – стороной основания и высотой
пирамиды, выраженных в локтях.
Слайд 22
«Большой Лувр» после
реставрации в 1981 г.
Связь между новыми
залами
и двором осуществляется с помощью пирамиды из прозрачного
стекла необычайно легкой конструкции.Автором этого новаторского
проекта был американский
архитектор китайского
происхождения Ео Минг Пей.
Слайд 23 Французский ученый Жак Бержье, изучавший влияние различных пространственных
форм на биологические вещества, соорудил картонную модель Пирамиды и
поместил туда бычью кровь. Через некоторое время она разделилась на две субстанции - светлую и темную. Другие ученые удостоверились, что в модели Пирамиды долго сохраняются скоропортящиеся продукты. Маятник, подвешенный над вершиной модели, отклоняется в сторону или медленно вращается вокруг вершины. Странно ведут себя и растения. Сначала они тяготеют к востоку, потом описывают полукруг, двигаясь с юга на запад. Чешский изобретатель Карел Дрбал в 1959 году приспособил подобную модель для самозатачивания бритвенных лезвий, и получил патент на это необычное изобретение.! Считается, что пирамидальная форма фокусирует космическую энергию...Биологическое воздействие
Слайд 24
Задания
1.Сколько граней, вершин, ребер у n-угольной пирамиды?
2.Какое наименьшее
число граней, вершин, ребер может иметь пирамида?
3.Высота пирамиды
равна 3см. Чему равно расстояние от вершины пирамиды до плоскости основания? 4.Какие многоугольники могут быть сечением 4-х угольной пирамиды?
5.Боковые ребра треугольной пирамиды равны 7см, 12см и 5см. Одно из них перпендикулярно к плоскости основания. Чему равна высота пирамиды?
6.Одно из боковых ребер пирамиды равно 12см, а ее высота – 6см. Найдите угол между этим ребром и плоскостью основания пирамиды.
7.Все плоские углы при вершине треугольной пирамиды прямые, а выходящие из нее ребра равны 2м, 4м и 6м.Найдите площадь боковой поверхности пирамиды.
8.Основание пирамиды – правильный 6-ти угольник. Найдите величину угла, образованного двумя гранями пирамиды, если их общее ребро перпендикулярно к плоскости основания.
9.Основание пирамиды – 4-х угольник все стороны которого равны. Высота пирамиды проходит через точку пересечения диагоналей основания. Является ли данная пирамида правильной?
10.Сторона основания правильной 6-ти угольной пирамиды равна 1м, а боковое ребро – 2м. Найдите: а) высоту пирамиды б) угол между боковым ребром и плоскостью основания пирамиды.
11.Сторона основания правильной 4-х угольной пирамиды равна 6м, а боковое ребро – 5м. Найдите: а) апофему б) площадь боковой поверхности пирамиды.





























