Презентация на тему Динамическое описание систем. Фильтрация Калмана

3

2. Анализ свойств Фильтра Калмана 9
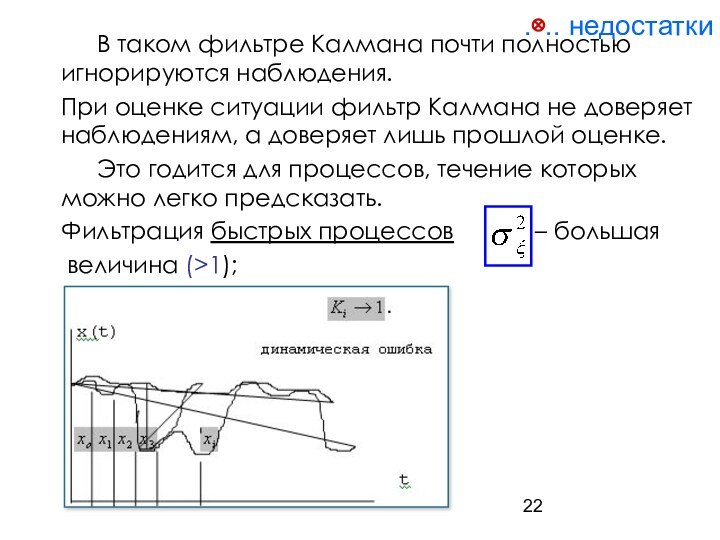
2.1 Фильтрация медленных процессов

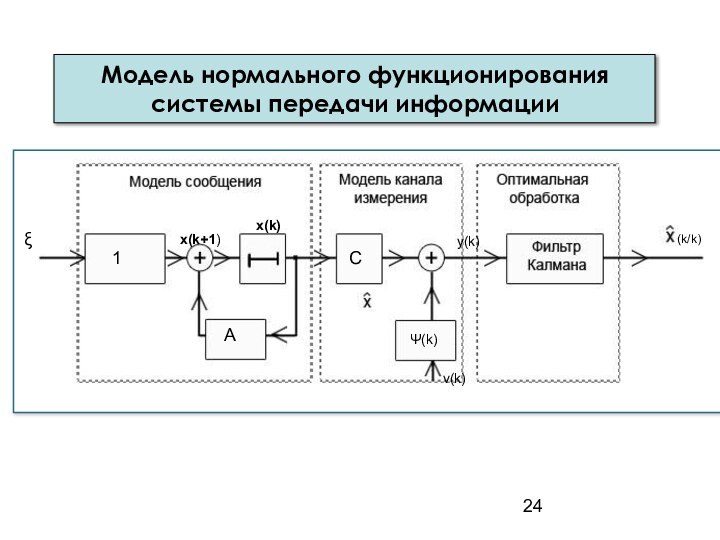
3. Модель нормального функционирования системы передачи информации

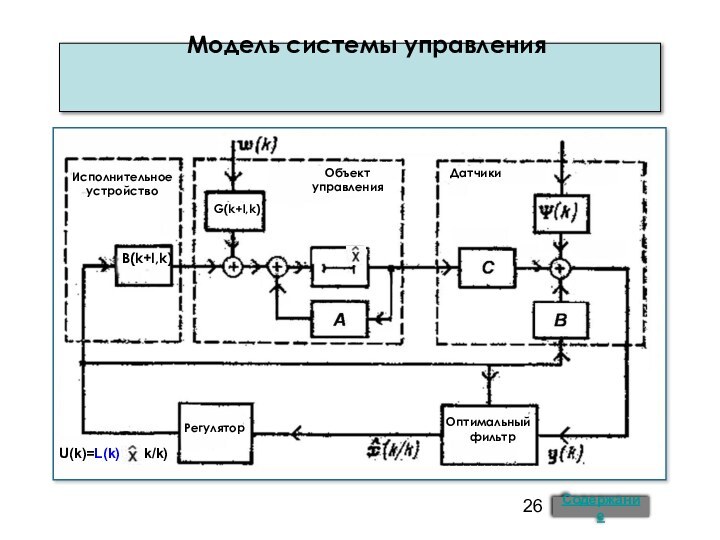
4. Модель системы управления 11

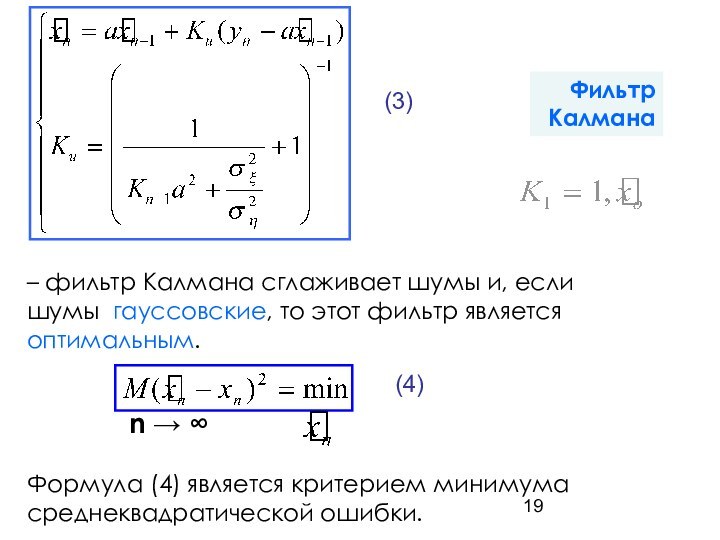
5. Основные особенности фильтра Калмана 15

6. Вычислительная схема Фильтра Калмана 16

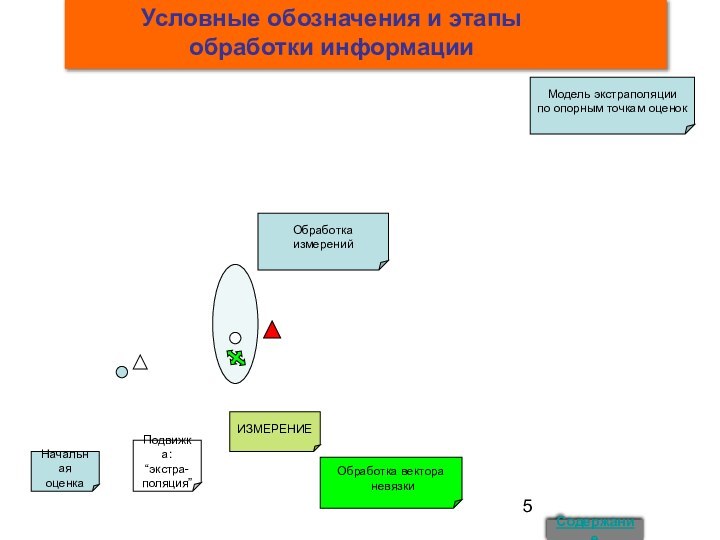
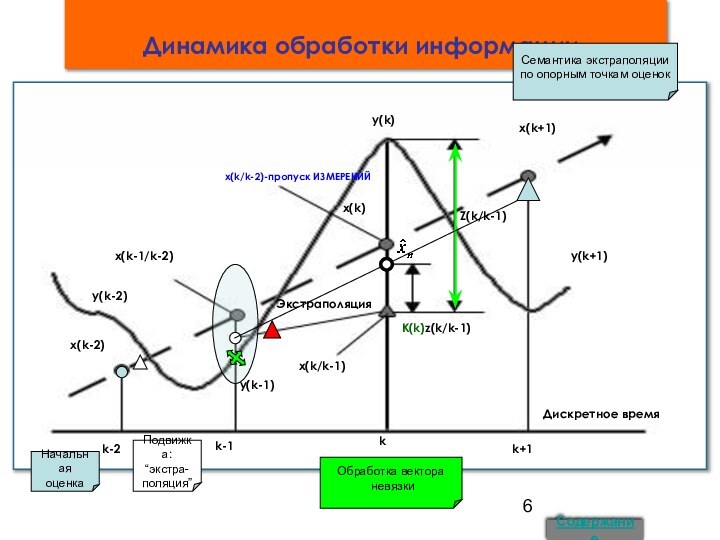
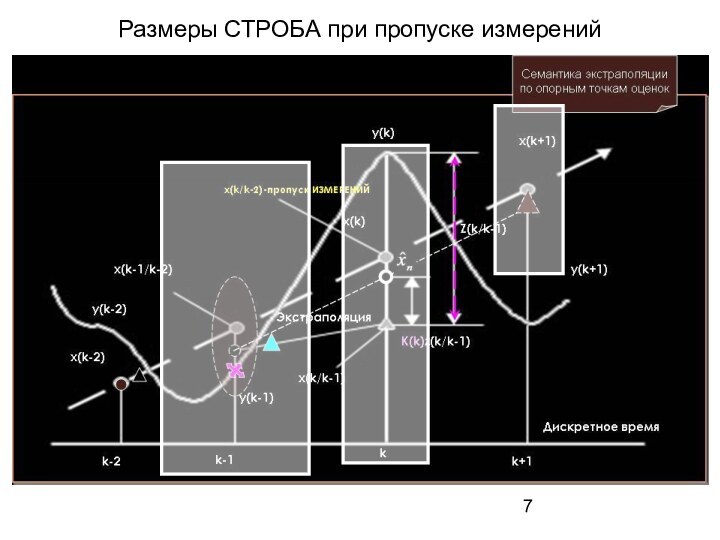
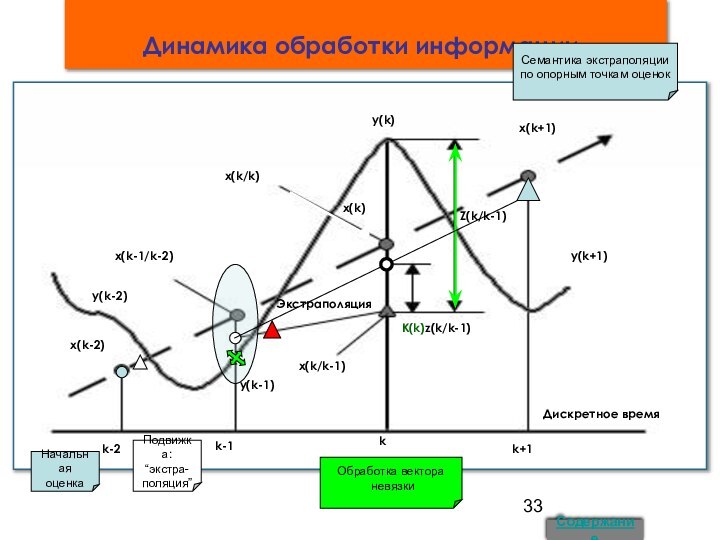
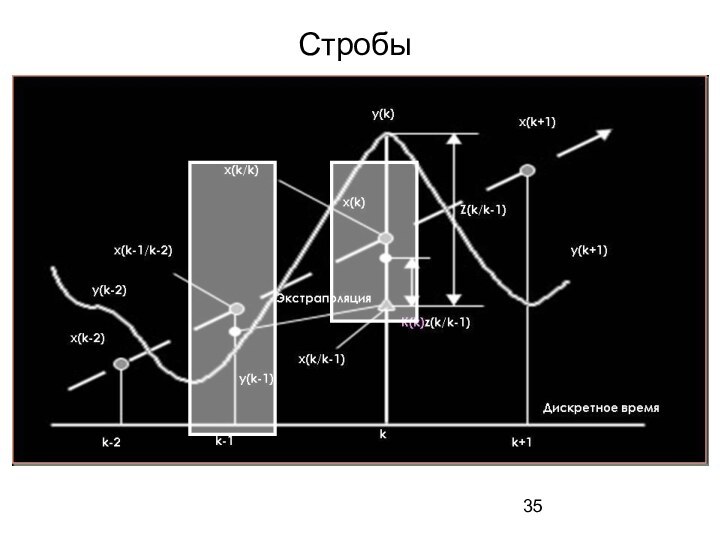
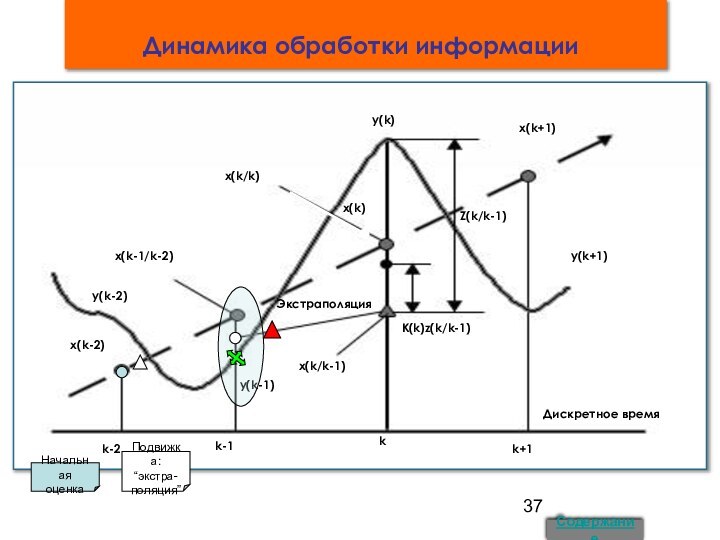
7. Динамика обработки информации 17
+Пример реализации фильтра Калмана

Содержание

(зеленые точечки)
модель движения – вектор скорости позволяет указать

центр строба
? Δ
РЕКУРРЕНТНАЯ ОБРАБОТКА:
Очередная оценка;
Улучшенная экст-раполяция,
Обработка невязки
ЗАДАЧИ: уметь дать графические
интерпретации

обозначения и этапы обработки информации

точкам оценок

него легко перейти к передаточной функции W(p) с помощью

однозначного преобразования
C (p I – A)–1 B:

Итак,

Фильтр Калмана дает описание преобразований не в частотной, а во временной области

с помощью дифференциальных или разностных уравнений.

Наш пример предполагает, что

наблюдения и измерения проводятся в условиях шума. Как правило, принимается модель нормального закона распределения шума.
Для уяснения характера математической постановки формирования оценок рассмотрим случай одномерной динамической системы. Матрица А представлена числом а.
Матрица С, выделяющая наблюдаемые состояния отражена одиночным множителем 1
Уравнения движения и измерения имеют только по 2 слагаемых

(1) Одномерные
динамические системы

Содержание

методом наименьших квадратов.
Вводится эмпирический риск :

– классическая формулировка метода наименьших квадратов . Эмпирическим риск назван так потому, что в риск входят наблюдения.
Согласно формуле (2) требуется минимизировать риск, и следовательно уменьшить влияние шумов.

(2)

Необходимо так выбрать xi, чтобы получить минимум по всей

траектории. Набор оценок, соответствующий оптимальной траектории, будем обозначать



Он получается путем дифференцирования

Проделав математические операции получаем одномерный фильтр Калмана.

гауссовские, то этот фильтр является оптимальным.




Формула (4) является критерием

минимума среднеквадратической ошибки.

Фильтр Калмана

n → ∞

(3)

(4)

для гауссовских шумов, оптимальную по критерию (4) –

по критерию минимума среднеквадратической ошибки.
Замечание 1 : Оптимальность означает, что не существует другого фильтра, который мог бы дать такие же результаты по среднеквадратической ошибке. (Остальные фильтры дают большую ошибку)

Замечание 2 : Фильтр Калмана реализуется на ЭВМ во временной области, а не в частотной

,
х(t) есть медленный процесс, тогда


что следует из формулы (3)
В этом случае - ФК осуществляет преимущественно
экстраполяцию(прогноз),т.е.прошлая и текущая оценки почти одинаковы.

Фильтрация медленных процессов

наблюдения.
При оценке ситуации фильтр Калмана не доверяет наблюдениям,

а доверяет лишь прошлой оценке.
Это годится для процессов, течение которых можно легко предсказать.
Фильтрация быстрых процессов – большая
величина (>1);

наблюдениям. Это значит, что фильтр Калмана не доверяет прошлым

оценкам.
Вывод : Фильтр Калмана минимизирует и флуктуационную и динамическую ошибку.

. ⊗.. недостатки

в качестве своей компоненты передаваемое сообщение. Это сообщение (например,

траектория сопровождаемой цели в радиолокации) моделируется в виде случайного процесса, полученного путем пропускания бело­го гауссовского шума через линейный фильтр в общем случае с зависящими от времени параметрами (эти параметры определяются переходными матрицами системы и шумов возмущений). В канале измерения на сигнал, полу­ченный путем линейного преобразования вектора состояния , аддитивно накладывается шум измерений прошедший предварительно безинерционное линейное преобразование с матрицей . Задача оптимального выделения принятого сообщения из наблюдаемого сигна­ла у в соответствии с критерием минимума среднего значения квадрата ошибки решается с помощью устрой­ства оптимальной обработки, представляющего в рассматриваемом случае фильтр Калмана .

фильтр
U(k)=L(k) (k/k)
Содержание

aik = L(k)j.(k\k), где x(fc|ft)
оптимальная

оценка вектора состояния, получаемая на выходе фильтра Калмана — оператор оптимального регулятора. Основными задачами исследования ДС являются синтез алгоритмов оптимальной фильтрации и управления при известных динамических свойствах системы и заданных характеристиках канала измерения.

канал измерения. Нарушения в канале измерения могут происходить но

целому ряду причин, основными из которых являются:
случайные пропадания информационных сигналов; появление ложных (аномальных) измерений y(k);
резкое возрастание шумов измерений v(k) или случайное изменение их характеристик.

Использование при этих условиях алгоритмов оценивания, не учитывающих возможности появления нарушений канале измерения, приводит к существенному возрастанию ошибок фильтрации, а в задачах сопровождения целей — к срыву слежения.

для реализации на ЭВМ, алгоритм вычисления оценки состояния ДС

при полностью известной ее модели;

оценка, получаемая с помощью этого фильтра, является линейной относительно наблюдений;

корреляционная матрица ошибок фильтрации P(k/k) вследствие линейности фильтра не зависит от наблюдений y(k)и, следовательно, может быть вычислена заранее;

Содержание

систем);

так как параметры фильтра Калмана изменяются во времени, то

такой фильтр минимизирует среднеквадратическое значение ошибки оценивания не только в установившемся режиме, но и в течение переходного процесса.

P(k/k)
P (k/k-1)
P(k-1/k-1)
P(k/k)
Установка начального
значения x(0)
Априорные данные
R(k)
Q(k)
x (k-1/k-1)
x(k/k-1)
u(k)
Установка начального

значения P0

K(k)

Содержание

точкам оценок

оценок

оценок