Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Моделирование ценовой политики

Содержание

Имеем уравнение Вида
Кафедра математики и моделированияСтарший преподаватель Е.Г. ГусевКурс «Высшая математика»Лекция 23. Тема: Моделирование Система из линейного уравнения (1) Относительно (n+1) неизвестного в матричной форме запишется Таким образом, увеличение цены на n-й товар привело к следующему изменению спроса на товары: Рассмотрим такое увеличение дохода на dM, которое компенсирует потребителю увеличение цены на dpn. Условие постоянства полезности Теперь можем определить dM, используя : то есть доход Которые в матричной форме примут вид: Решение уравненийнаходим с помощью обратной матрицы: Таким образом, увеличение цены с компенсацией дохода приводит к следующему изменению спроса: получаем уравнение Слуцкого, которое является стержнем теории полезности: Ценный и малоценный товар Товар i называется ценным если при увеличении дохода Валовой заменитель продукта Продукт L называется валовым заменителем продукта i если Функция спроса Х*(р;м) обладает свойством валовой заменимости, если с увеличение цены на Вопросы:1)Какие составляющие решения ценовой политики?2)В чем заключается свойство валовой заменимости?
Слайды презентации

Слайд 2

Имеем уравнение Вида


Имеем уравнение

Вида

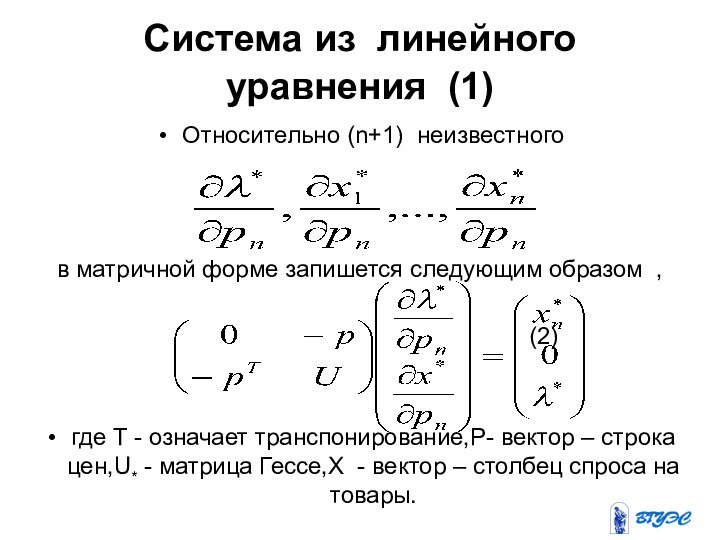
Слайд 3 Система из линейного уравнения (1)

Относительно (n+1) неизвестного


Система из линейного уравнения (1) Относительно (n+1) неизвестного в матричной форме


в матричной форме запишется следующим образом ,

(2)


где Т - означает транспонирование,Р- вектор – строка цен,U* - матрица Гессе,X - вектор – столбец спроса на товары.

Слайд 4 Таким образом, увеличение цены
на n-й товар привело к

Таким образом, увеличение цены на n-й товар привело к следующему изменению спроса на товары:

следующему изменению спроса на товары:

Слайд 5 Рассмотрим
такое увеличение дохода на dM, которое компенсирует потребителю

Рассмотрим такое увеличение дохода на dM, которое компенсирует потребителю увеличение цены на

увеличение цены на dpn. Согласно теории потребления это означает,

что полезность потребителя сохранилась на прежнем уровне, то есть dun=0.
Используя получим

Слайд 6 Условие постоянства полезности
Теперь можем определить dM, используя

Условие постоянства полезности Теперь можем определить dM, используя : то есть доход


:
то есть доход вырос ровно на столько, сколько

необходимо было бы дополнительно затратить потребителю на приобретение n-го товара в прежнем объеме при увеличении цены на dpn.

Слайд 7 Которые в матричной форме примут вид:

Которые в матричной форме примут вид:

Слайд 8 Решение уравнений
находим с помощью обратной матрицы:

Решение уравненийнаходим с помощью обратной матрицы:

Слайд 9 Таким образом, увеличение цены с компенсацией дохода приводит

Таким образом, увеличение цены с компенсацией дохода приводит к следующему изменению спроса:

к следующему изменению спроса:

Слайд 10




получаем уравнение Слуцкого, которое является стержнем теории полезности:

получаем уравнение Слуцкого, которое является стержнем теории полезности:

Слайд 11 Ценный и малоценный товар

Товар i называется ценным

Ценный и малоценный товар Товар i называется ценным если при увеличении

если при увеличении дохода спрос на него растет


и

малоценным, если

Слайд 12 Валовой заменитель продукта
Продукт L называется валовым заменителем

Валовой заменитель продукта Продукт L называется валовым заменителем продукта i если

продукта i если

Слайд 13 Функция спроса Х*(р;м) обладает свойством валовой заменимости, если

Функция спроса Х*(р;м) обладает свойством валовой заменимости, если с увеличение цены

с увеличение цены на любой продукт I спрос на

остальные продукты не убывает
если же , то функция спроса обладает свойством сильной валовой заменимости.
  • Имя файла: modelirovanie-tsenovoy-politiki.pptx
  • Количество просмотров: 98
  • Количество скачиваний: 0
- Предыдущая Город Жердевка
Следующая - Отрывки из сочинений

Похожие презентации

Конспект урока по математике Числовое равенство и уравнение, 2 класс УМК Перспективная начальная школа план-конспект урока по математике (2 класс) Конспект урока по математике Числовое равенство и уравнение, 2 класс УМК Перспективная начальная школа план-конспект урока по математике (2 класс) 117
Розв'язування складених задач різними способами. Розв’язування рівнянь. Знаходження периметра геометричних фігур Розв'язування складених задач різними способами. Розв’язування рівнянь. Знаходження периметра геометричних фігур 93
Презентация по математике кроссворд Презентация по математике кроссворд 122
Открытый урок 5 кл Среднее Арифметичексое Открытый урок 5 кл Среднее Арифметичексое 159
Презентация к уроку математики 1 класс по теме Сложение с нулем презентация к уроку (математика, 1 класс) по теме Презентация к уроку математики 1 класс по теме Сложение с нулем презентация к уроку (математика, 1 класс) по теме 116
ТРЕНАЖЕРЫ ПО МАТЕМАТИКЕ ДЛЯ ПОДГОТОВКИ К ЕГЭ 2015 ТРЕНАЖЕРЫ ПО МАТЕМАТИКЕ ДЛЯ ПОДГОТОВКИ К ЕГЭ 2015 124
Теория вероятностей и математическая статистика. Основные понятия. Классическое определение вероятности Теория вероятностей и математическая статистика. Основные понятия. Классическое определение вероятности 130
Линейные уравнения 2-го порядка с постоянными коэффициентами Линейные уравнения 2-го порядка с постоянными коэффициентами 149
Тренажёр по математике 3 класс Умножение на 10, 100 и 1000 тест по математике (3 класс) Тренажёр по математике 3 класс Умножение на 10, 100 и 1000 тест по математике (3 класс) 140
Консультация для родителей по математике консультация по математике по теме Консультация для родителей по математике консультация по математике по теме 128
Закрепление изученного по теме Нумерация чисел от 11 до 20. план-конспект урока по математике (1 класс) Закрепление изученного по теме Нумерация чисел от 11 до 20. план-конспект урока по математике (1 класс) 148
Урок математики в 1 классе план-конспект урока (математика, 1 класс) Урок математики в 1 классе план-конспект урока (математика, 1 класс) 106
Презентация проекта Математика на кухне проект по математике (старшая группа) Презентация проекта Математика на кухне проект по математике (старшая группа) 178
10 10 189
урок математики 1 класс Вычитание из 10 план-конспект урока по математике (1 класс) по теме урок математики 1 класс Вычитание из 10 план-конспект урока по математике (1 класс) по теме 133
Задачи на умножение (2 класс) Задачи на умножение (2 класс) 151
Открытый банк заданий по математике Задача №14 Открытый банк заданий по математике Задача №14 120
Методическая разработка по математике на тему Решение уравнений Методическая разработка по математике на тему Решение уравнений 117
Жас матиматиктер сайыс (6 сынып) Жас матиматиктер сайыс (6 сынып) 219
Презентация к уроку математики 4 класс Единицы времени Презентация к уроку математики 4 класс Единицы времени 118
Приёмы устного решения квадратного уравнения 8 класс Приёмы устного решения квадратного уравнения 8 класс 95
Графики функций Графики функций 117
Понятие вектора. Длина и направление вектора. Равенство векторов Понятие вектора. Длина и направление вектора. Равенство векторов 103
Деление на 1 000, 10 000, ... Деление на 1 000, 10 000, ... 140
Исследовательская работа:Математика в Древней Руси презентация к уроку по математике (4 класс) Исследовательская работа:Математика в Древней Руси презентация к уроку по математике (4 класс) 205
Решение комбинаторных задач Решение комбинаторных задач 135
Сенсорное развитие. Дидактические игры по сенсорному воспитанию детей раннего и младшего дошкольного возраста. презентация к уроку по математике (младшая группа) Сенсорное развитие. Дидактические игры по сенсорному воспитанию детей раннего и младшего дошкольного возраста. презентация к уроку по математике (младшая группа) 135
Презентация к уроку математики во 2 кл. : Квадрат. презентация к уроку по математике (2 класс) Презентация к уроку математики во 2 кл. : Квадрат. презентация к уроку по математике (2 класс) 113
2 prezentaciya kollichestvennyy schet 2 2 prezentaciya kollichestvennyy schet 2 117
Презентация урока по математике(5 класс) Презентация урока по математике(5 класс) 149