- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии на тему Теорема о площади треугольника
Содержание
- 2. Цели урока:актуализировать знания учащихся о площади треугольника,
- 3. Вспомним все формулы для
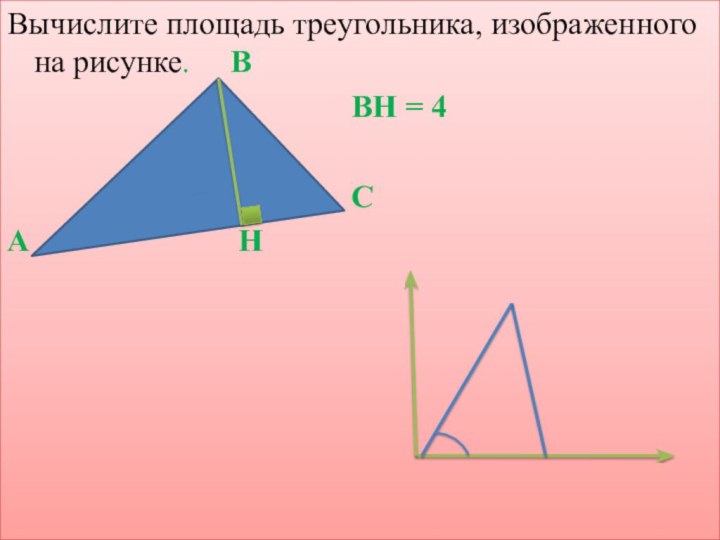
- 4. Фронтальная работа с классомВычислите площадь треугольника, изображенного
- 5. Вычислите площадь треугольника, изображенного на рисунке.
- 6. Изучение новой темыЗадача.
- 7. Закрепление изученного материала1. Самостоятельно решить задачи №
- 8. Проверка№1020 (а) Решение:АВ = 6√8 см, АС = 4см,
- 9. Дополнительные задачи 1. Найдите площадь равнобедренного треугольника
- 10. 2. В треугольнике АВС АВ =
- 11. Скачать презентацию
- 12. Похожие презентации
Цели урока:актуализировать знания учащихся о площади треугольника, полученные в 8 классе;доказать теорему о площади треугольника;научить решать задачи на применение теоремы о площади треугольника;









Слайд 2
Цели урока:
актуализировать знания учащихся о площади треугольника, полученные
в 8 классе;
на применение теоремы о площади треугольника;Слайд 3 Вспомним все формулы для
вычисления площади треугольника
1.Формула для вычисления площади прямоугольного
треугольника.S = ½ ав
2.Формула для вычисления площади произвольного треугольника.
S = ½ аh
3.Формула Герона.
S =√p (p – a) (p – b) (p – c)
Слайд 4
Фронтальная работа с классом
Вычислите площадь треугольника, изображенного на
рисунке.
А
А В5 5 6
В С В С А 60° С
3 7 8
Слайд 6
Изучение новой темы
Задача.
у В
В ΔАВС ВС = а, АС = b, <С = α . Найдите площадь треугольника.
Решение:
α
Координаты точки В равны: х = а sinα, у = а cosα о Н х
Высота ΔАВС, проведенная к стороне АС, равна ВН. С другой стороны, ВН – это ордината точки В, т.е. ВН = а sinα.
S = ½ АС · ВН = ½ b · (a · sinα) = ½ ab sinα.
Итак,
S = ½ ab sinα
где а,b – стороны треугольника, α – угол между ними.
Слайд 7
Закрепление изученного материала
1. Самостоятельно решить задачи № 38,
№ 39 из рабочей тетради.
2. Самостоятельно
решить задачи :I уровень - №1020 (а)
II уровень - №1022
Слайд 8
Проверка
№1020 (а)
Решение:
АВ = 6√8 см, АС
= 4см,
АВ·АС· sin60° = ½· 6√8 ·4· = 12√6 см²Ответ: 12√6 см²
№1022
Решение:
SАВС = ½ АВ·АС· sin<А
SАВС = 60см², АС = 15 см, <А = 30° АВ = = 16 см.
Ответ: 16 см.
Слайд 9
Дополнительные задачи
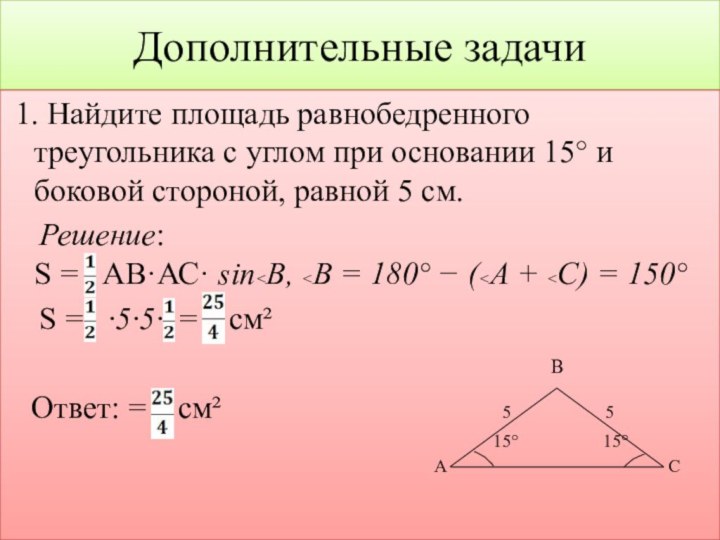
1. Найдите площадь равнобедренного треугольника с
углом при основании 15° и боковой стороной, равной 5
см.Решение: S = АВ·АС· sin<В, <В = 180° − (<А + <С) = 150°
S = ·5·5· = см²
В
Ответ: = см² 5 5
15° 15°
А С
Слайд 10 2. В треугольнике АВС АВ = 4,
ВС = 6,
ВD −
биссектриса, < АВС = 45°. Найдите площади треугольников АВD и CBD. Решение:
SАВС = АВ·ВС·sin45° = ·4·6· = 6√2.
BD – биссектриса АВС, тогда
.
Так как S ΔABC = 6√2 = S ΔABD + S ΔCBD, = ,
то S ΔABD = , S ΔCBD = .
Ответ: ,