Слайд 2
"ЧИСЛА ПРАВЯТ МИРОМ
ЧЕРЕЗ СВОЙСТВА
ПИФАГОР
ГЕОМЕТРИЧЕСКИХ ФИГУР".
Начальные
геометрические
сведения.
Введение в геометрию.
Точка, прямая и отрезок.
Слайд 4
Евклид (Eνκλειδηζ) (365-300 до н.э.) древнегреческий математик ,
автор первого из дошедших до нас теоретических трактатов по
математике «Начала» (13 книг).
Евклид. Рельеф работа Андреа Пизано. Около 1334-1340 г.г.
Слайд 5
Страницы «Начал» Евклида.
Издание 1482 г.
Слайд 6
Платон (477-347 до н.э.) -
древнегреческий философ, ученик Сократа и учитель Евклида.
Многих мыслителей и философов привлекала знаменитая Академия Платона. Уважение
к геометрии было настолько велико, что по преданию, у входа в Академию Платона имелась надпись:
«Не знающий геометрию
да не входит!»
Птолемей I сам захотел одолеть премудрости геометрии, но довольно
скоро обнаружил, что изучение математики – слишком тяжелое бремя. Птолемей спросил Евклида: «Нельзя ли постигнуть все тайны науки как-нибудь проще?»
Евклид ответил:
«В геометрии нет царского пути!»
Слайд 9
Евдем Родосский
(IV век до
н.э.)
объясняет происхождение термина «геометрия» так: «Геометрия была открыта египтянами и возникла при измерении Земли. Это измерение было им необходимо вследствие разлития реки Нила, постоянно смывавшего границы».
Слайд 10
от древнегреческих слов
«ge»- «земля» и «metreo»- «измеряю»
Геометрия
– это наука, занимающаяся изучением геометрических фигур и их
свойств.
Какие геометрические фигуры вам известны?
прямая куб
ломаная цилиндр
отрезок шар
луч конус
прямоугольник пирамида
квадрат параллелепипед
По какому принципу данные геометрические фигуры записаны в двух различных группах?
Геометрия
прямая
куб
ломаная цилиндр
отрезок шар
луч конус
прямоугольник пирамида
квадрат параллелепипед
Часть геометрии, в которой рассматриваются фигуры
НА ПЛОСКОСТИ В ПРОСТРАНСТВЕ
Называется
Planum (лат) –
равнина, местность Sterio (лат) -
телесный, пространственный
(в 7-9 классах) (в 10-11 классах)
Геометрия
стереометрия
планиметрия
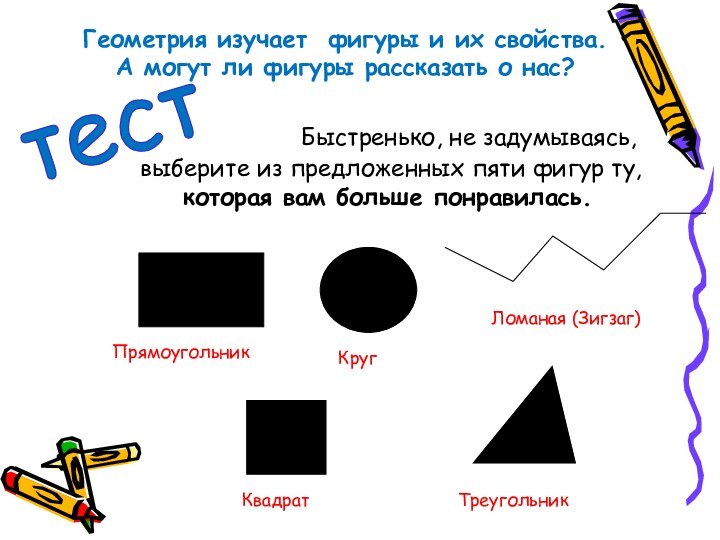
Быстренько, не задумываясь,
выберите из предложенных пяти фигур
ту,
которая вам больше понравилась.
Прямоугольник
Круг
Ломаная (Зигзаг)
Квадрат
Треугольник
тест
Геометрия изучает фигуры и их свойства.
А могут ли фигуры рассказать о нас?
Слайд 13
Вот что говорят фигуры о нас
Соответствует трудолюбие,
усердие, потребность доводить начатое дело до конца, упорство. Любит
раз и навсегда заведенный порядок.
Это временная форма личности, ищет лучшее положение. Поэтому любознателен, пытлив, интересно все происходящее, и смел.
Символ лидерства. Способен концентрироваться на главной цели. Энергичен, неудержим, сильная личность.
Самая доброжелательная фигура. Способен сопереживать, сочувствовать. Счастлив тогда, когда все ладят друг с другом.
Символ творчества. Нравится комбинировать, создавать что-то новое, оригинальное. Самый восторженный и возбудимый.
Слайд 14
Фигуры много знают о нас.
Поэтому и мы
должны узнать о них как можно больше.
Что же мы будем изучать в 7 классе?
Глава 1. Начальные геометрические
сведения.
Глава 2. Треугольники.
Глава 3. Параллельные прямые.
Глава 4. Соотношения между сторонам
и углами треугольника
Логическая цепочка:
начальные понятия –определения –
аксиомы - теоремы
Поможет нам в этом – учебник. Авторы нашего учебника: Л. С. Атанасян, В. Ф. Бутузов, С, Б. Кадомцев, Э. Г. Позняк, И. И. Юдина.
Слайд 15
– гимнастика для ума
- витамин
для мозга
- язык геометрии
Без чертежа не изготовить ни одной машины, не построить здания. На нем можно изъясняться, не прибегая к словам. Древние математики часто рисовали чертеж и вместо доказательства писали только одно слово: «СМОТРИ!»
Архимед (287-212 до н.э.) – древнегреческий философ и ученый. Уроженец и гражданин Сиракуз (остров Сицилия). Образование получил в Александрии. Архимеду принадлежит ряд важнейших математических и физических открытий (закон Архимеда).
Математика
Геометрия
Чертеж
Слайд 16
Смерть Архимеда. Копия XVIII в. с римской мозаики
II в.
По преданию, последними словами Архимеда были:
«НЕ ТРОНЬ
МОИХ ЧЕРТЕЖЕЙ!».
Предание гласит: во II Пуническую войну во время обороны своего родного города Сиракузы Архимед придумал множество механических устройств, которые наводили ужас на нападавших римлян, таки не сумевших взять город приступом и победивших лишь с помощью предательства. В глубокой задумчивости Архимед рисовал на песке геометрические фигуры когда на него напали римские воины.
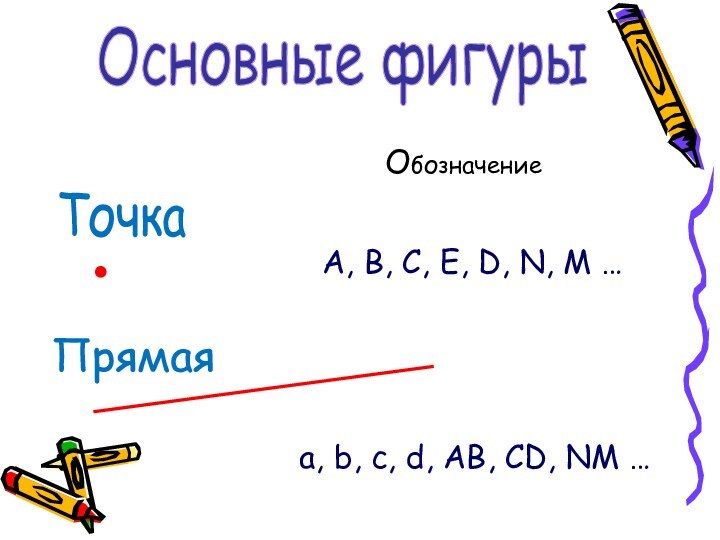
Обозначение . А, В, С, Е, D, N, M …
.
a, b, c, d, AB, CD, NM …
Основные фигуры
Точка
Прямая
Слайд 18
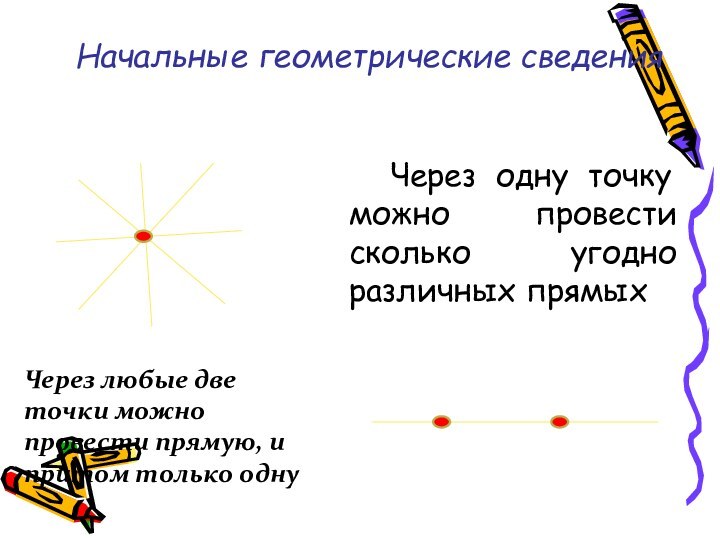
Начальные геометрические сведения
Через одну точку
можно провести сколько угодно различных прямых
Слайд 19
a
Начальные геометрические сведения
Слайд 20
Начальные геометрические сведения
Слайд 21
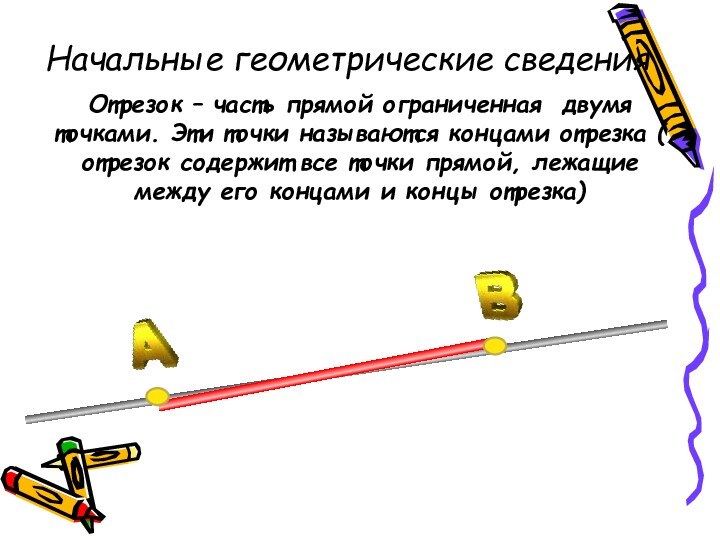
Отрезок – часть прямой ограниченная двумя точками. Эти
точки называются концами отрезка ( отрезок содержит все точки
прямой, лежащие между его концами и концы отрезка)
Начальные геометрические сведения
Слайд 22
Начальные геометрические сведения
A
C
M
O
AC
AM
AO
CM
CO
MO
Слайд 25
Начертите прямую.
Как ее можно
обозначить?
2. Отметьте точку
Т, не лежащую на данной прямой, и точки D,
E, K, лежащие на этой прямой.
Самостоятельная работа
Слайд 26
Специальные символы, позволяющие кратко записывать какое-либо утверждение.
є -
принадлежит, «лежит»
є - не принадлежит, «не лежит»
3. Используя
символы, запишите предложение:
«Точка D принадлежит прямой AB, точка C не принадлежит прямой a »
D є AB, C є a
Слайд 27
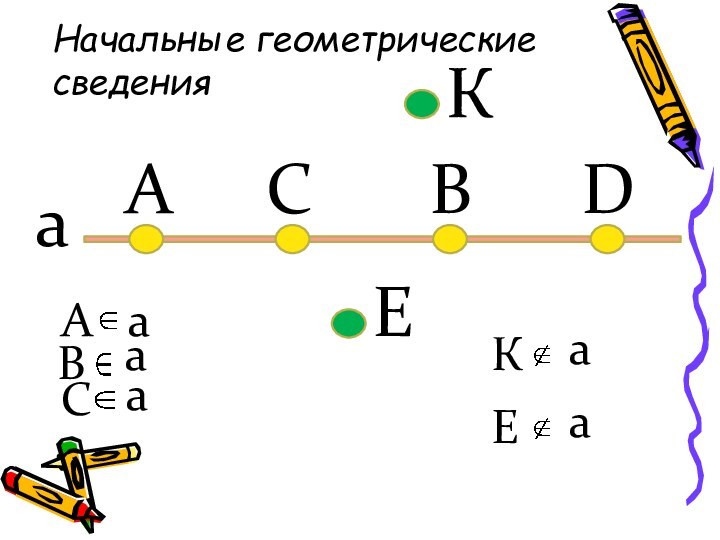
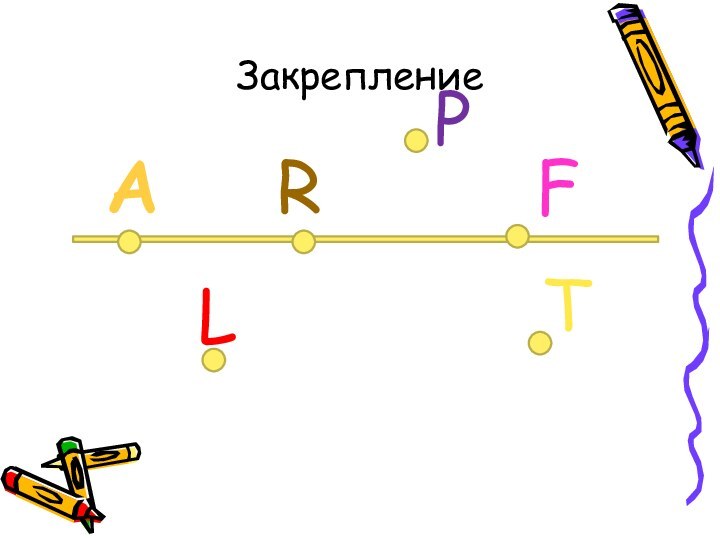
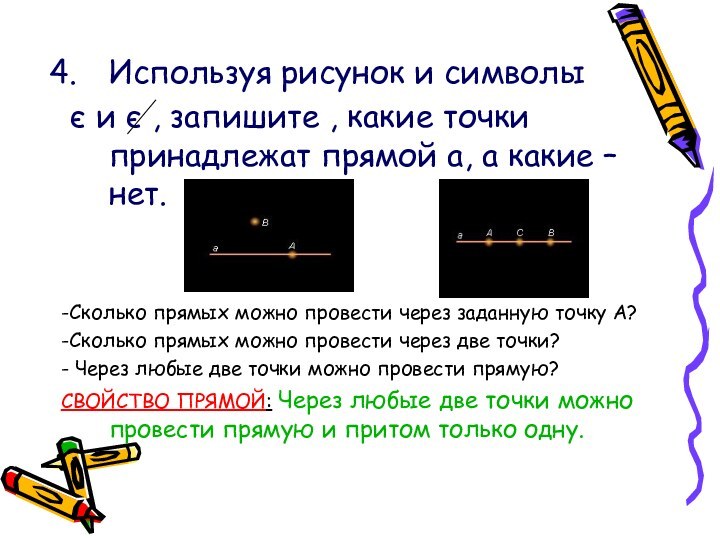
Используя рисунок и символы
є и є ,
запишите , какие точки принадлежат прямой а, а какие
– нет.
-Сколько прямых можно провести через заданную точку А?
-Сколько прямых можно провести через две точки?
- Через любые две точки можно провести прямую?
СВОЙСТВО ПРЯМОЙ: Через любые две точки можно провести прямую и притом только одну.
Слайд 28
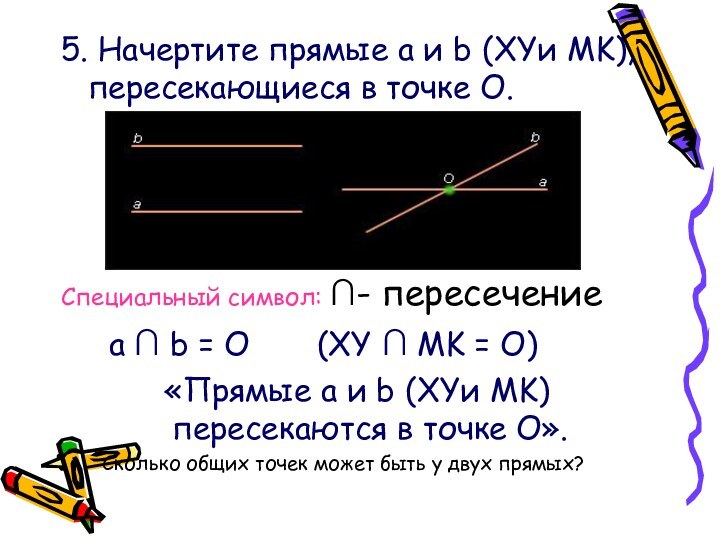
5. Начертите прямые a и b (XYи MK),
пересекающиеся в точке О.
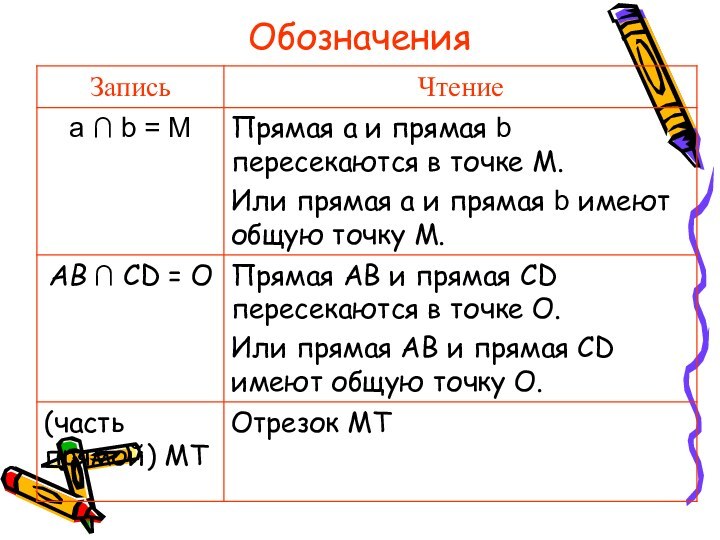
Специальный символ: ∩- пересечение
a ∩ b = О (XY ∩ MK = О)
«Прямые a и b (XYи MK) пересекаются в точке О».
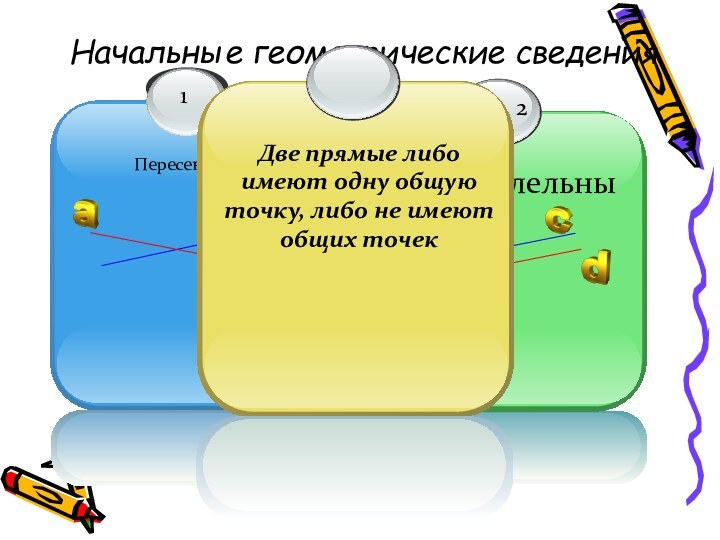
Сколько общих точек может быть у двух прямых?
Слайд 29
Задание:
сделать рисунки и обдумать ответ
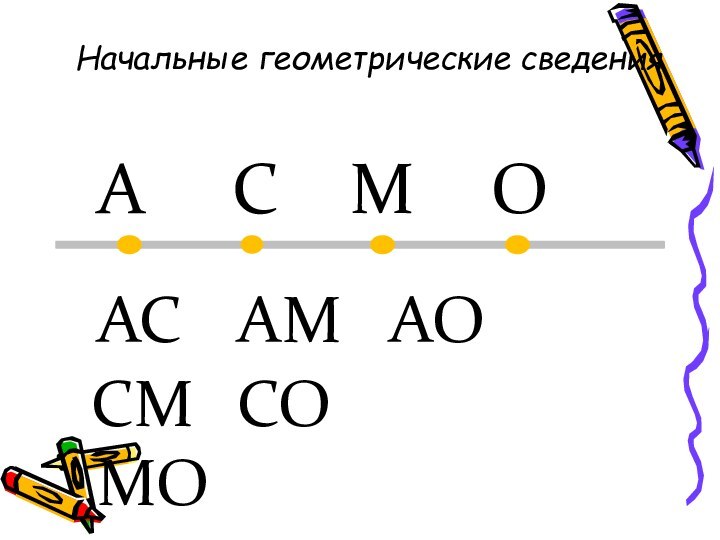
6. На прямой
a отметьте последовательно точки О, A, B, C.
Запишите все
получившиеся отрезки.
7. Начертите прямые a и b, пересекающиеся в точке М. На прямой a отметьте точку N, отличную от точки М.
Являются ли прямые М N и a различными прямыми?
Может ли прямая b проходить через точку N?
8. Дана прямая EF, A є EF, B є EF.
Может ли прямая АВ не пересекать
отрезок EF?
Слайд 30
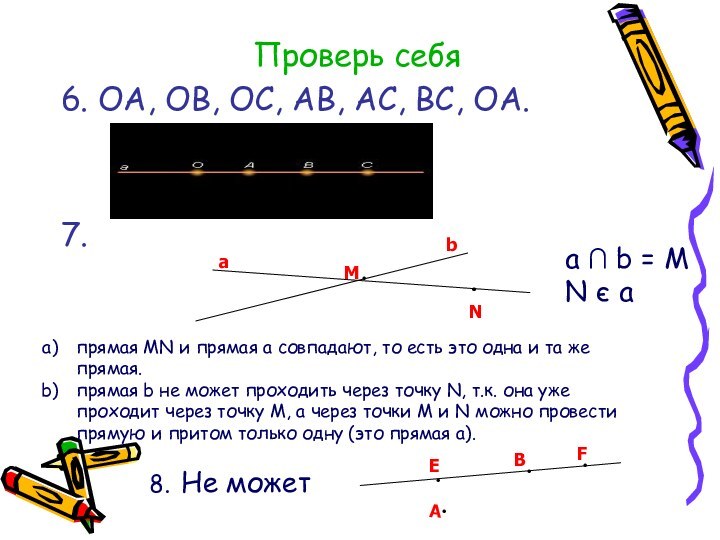
Проверь себя
6. ОА, ОВ, ОС, АВ, АС, ВС,
ОА.
7.
М
a
b
•N
•
a ∩ b = М
N є a
прямая МN
и прямая a совпадают, то есть это одна и та же прямая.
прямая b не может проходить через точку N, т.к. она уже проходит через точку M, а через точки М и N можно провести прямую и притом только одну (это прямая а).
8. Не может
•
•
•
•
А
Е
В
F
Слайд 31
На рисунке выделена
часть прямой,
ограниченная двумя
точками.
Как называется эта фигура?
Определение: часть прямой, ограниченная двумя точками,
называется отрезком. Точи, ограничивающие отрезок, называются его концами.
Обозначение: отрезок АС или СА
точки А и С – концы отрезка
Рассмотрите рисунок.
Что вы видите?
Запишите с помощью
символов.
О точке А, принадлежащей отрезку СB, говорят также, что точка А лежит между точками С и B (если А – внутренняя
точка отрезка), а также, что отрезок AС содержит
точку А.
Обозначение: С – А – В – «точка А лежит между
точками С и B »
Слайд 32
Решаем по учебнику:
страница 7 № 2,
5, 6.
Дополнительные задачи:
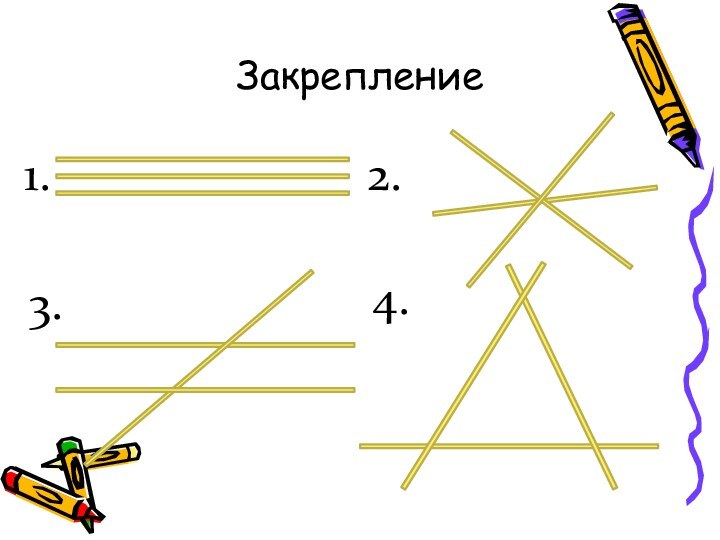
Сколько точек пересечения могут иметь три прямые?
Рассмотрите все возможные случаи и сделайте соответствующие рисунки.
На плоскости даны три точки. Сколько прямых можно провести через эти точки так, чтобы на каждой прямой лежали хотя бы две из данных точек? Рассмотрите все возможные случаи и сделайте рисунки.
Слайд 33
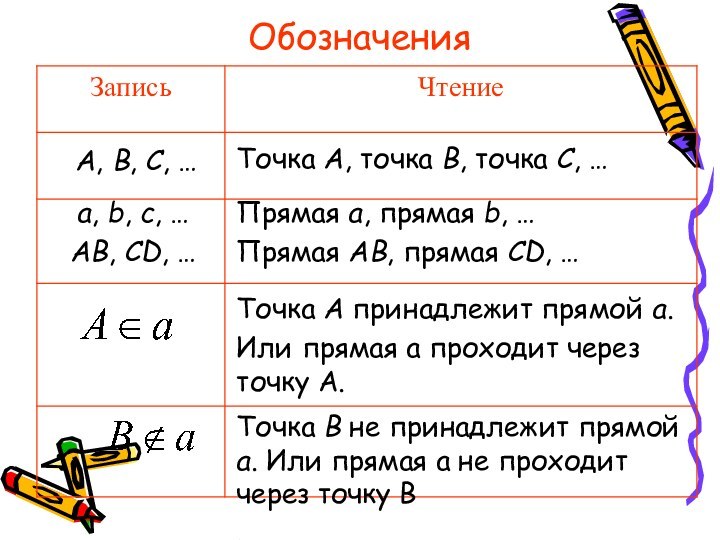
Обозначения
Точка A, точка B, точка C, …
A, B,
C, …
a, b, c, …
AB, CD, …
Прямая a, прямая
b, …
Прямая AB, прямая CD, …
Точка A принадлежит прямой a.
Или прямая а проходит через точку А.
Точка B не принадлежит прямой a. Или прямая а не проходит через точку В
.
Слайд 36
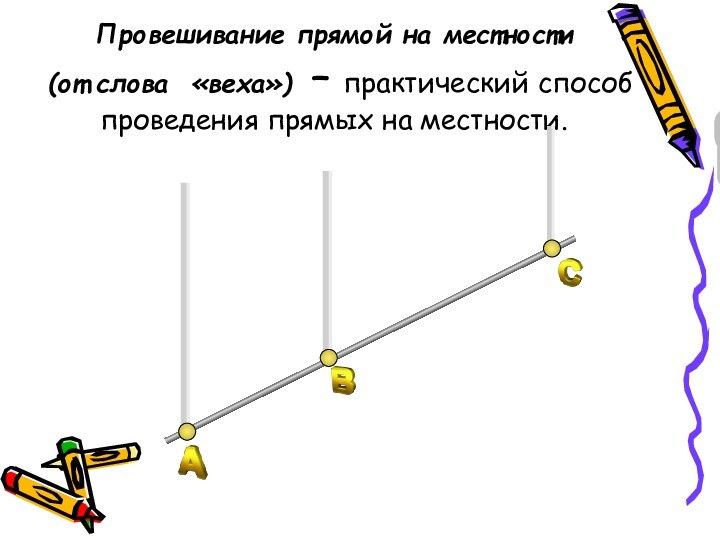
Провешивание прямой на местности
(от слова «веха»)
– практический способ проведения прямых на местности.
Слайд 37
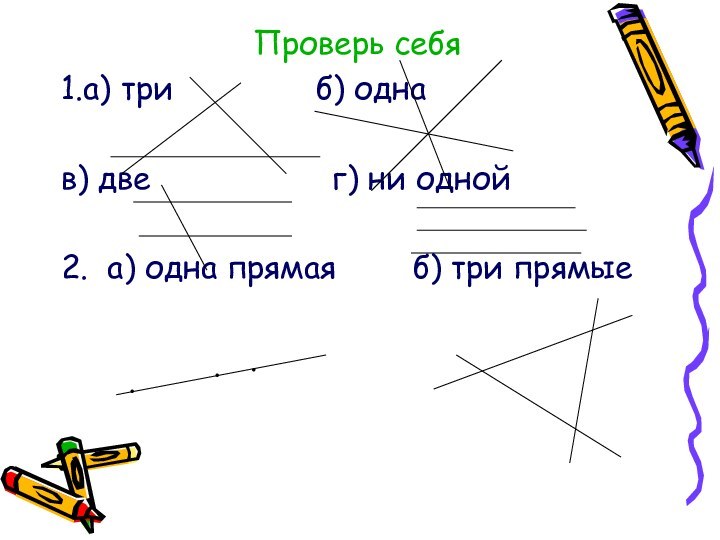
Проверь себя
1.а) три
б) одна
в) две
г) ни одной
2. а) одна прямая б) три прямые
•
•
•
Слайд 38
КРОССВОРД
Вставь пропущенное слово: «Через любые две точки можно
провести ... ; и при том только одну».
Математический знак
Название книги, в которой впервые был систематизирован геометрический материал.
Геометрическая фигура на плоскости.
Геометрическая фигура в пространстве.
Раздел геометрии.
Математический знак ∩
Первоначальное понятие в геометрии.
Часть прямой, ограниченная двумя точками.
Древнегреческий математик.
Геометрическая фигура на плоскости.
Слайд 39
Математический диктант
(с последующей проверкой).
1. Начертите прямую и
обозначьте ее буквой b.
а) Отметьте точку М, лежащую на
прямой b.
б) Отметьте точку N, не лежащую на прямой b.
в) Используя символы и , запишите предложение: "Точка М лежит на прямой b, а точка N не лежит на ней".
2. Начертите прямые а и b, пересекающиеся в точке М. На прямой а отметьте точку N, отличную от точки М.
а) Являются ли прямые MN и а различными прямыми?
б) Может ли прямая b проходить через точку N?
(Ответы обоснуйте)
Слайд 40
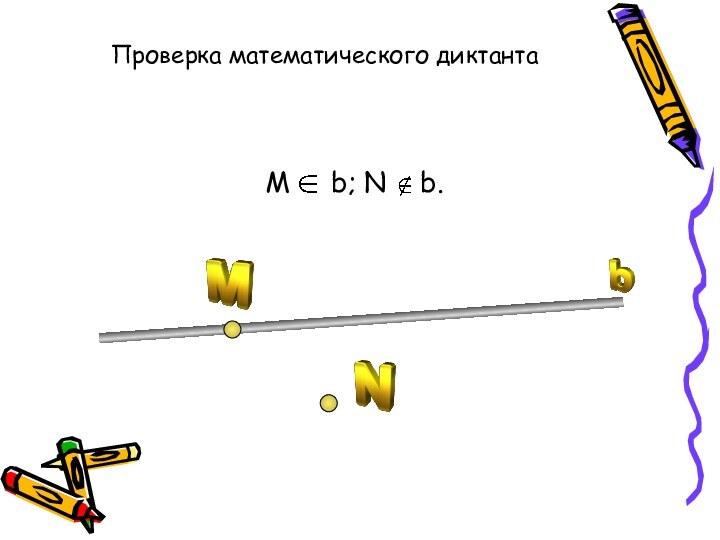
М b; N b.
Проверка математического
диктанта
Слайд 41
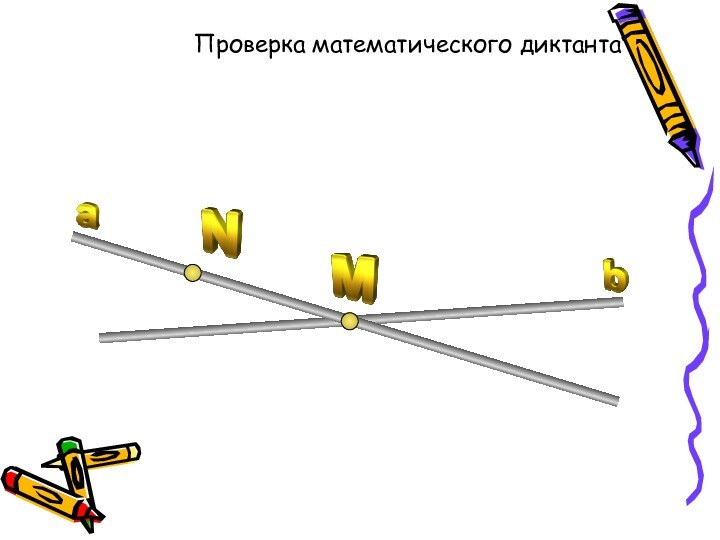
Проверка математического диктанта
Слайд 42
1. Параграф 1 учебника пункты 1 и 2
прочитать, подготовить ответы на вопросы 1, 2, 3 на
странице 25. Пункт 2 на уроке мы не рассматривали, дома самостоятельно с ним познакомитесь.
2. В тетради решить задачи № 1, 3, 4, 7.
3. Дополнительная задача (за нее можно получить хорошую отметку!)
Задача: Сколько различных прямых можно провести через четыре точки? Рассмотрите все возможные случаи и сделайте рисунки.
Запись домашнего задания
Слайд 43
Что узнали нового, чему научились, что понравилось.
Оцените
свою работу на уроке, нарисовав в тетради следующие знаки:
Старался,
и всё получалось.
Старался, но не всё получалось.
Не старался.
Что мы сегодня изучили на уроке