- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Начертательная геометрия. Проецирование прямой линии
Содержание
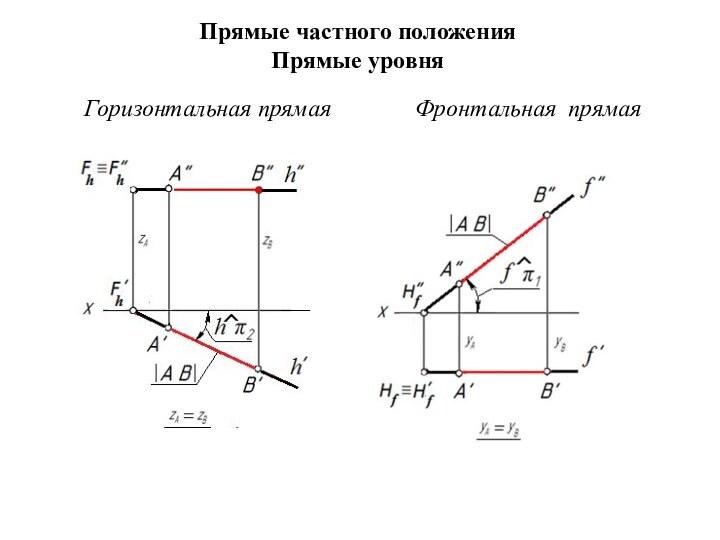
Прямые частного положения Прямые уровняГоризонтальная прямая Фронтальная прямая

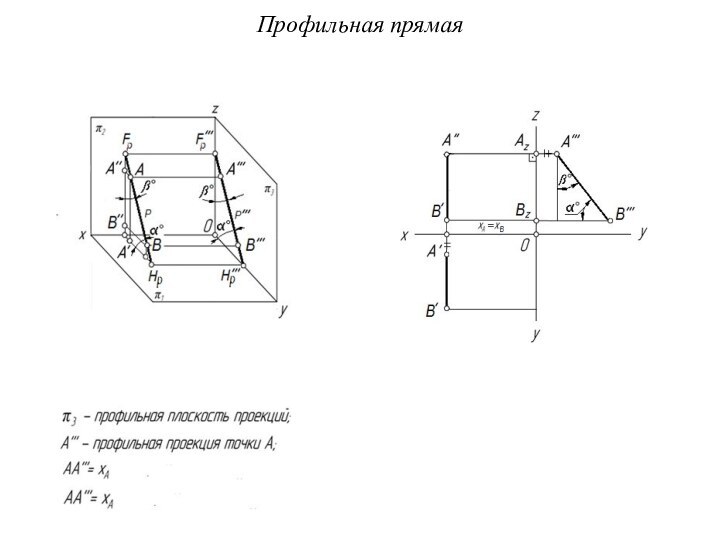




Слайд 4 В учебнике по геометрии (автор Атанасян Л.С. и
др. Геометрия для 10-11 кл. М.: Просвещение. 2009. 207
с.) приведена с доказательством задача №132): «Доказать, что если прямая параллельна плоскости, то все точки прямой равноудалены от плоскости Дано: Прямая a || α Доказать: все точки прямой a равноудалены от плоскости α. Доказательство Выберем на прямой a две произвольные точки А и В. Докажем, что расстояния от точки А и от точки В до плоскости α равны: ААα = ВВα. Если прямая a параллельна плоскости α, то в плоскости α содержится множество прямых, параллельных данной прямой a, например, прямая a1. Определим расстояния от точек А и В до плоскости α - ААα и ВВα: ААα α и ВВα α. Так как перпендикуляра к одной плоскости параллельны, то ААα || В Вα. Проведем АА1 || ВВ1, соединим точки Аα и А1 Вα и В1 и рассмотрим два равных треугольника - ААαА1 и ВВαВ1: АА1 = ВВ1 как отрезки параллельных прямых, заключенных между двумя другими параллельными прямыми; АαА1 = ВαВ1 как проекции равных наклонных. Из равенства треугольников следует, что ААα = ВВα – что и требовалось доказать.
Слайд 7
Правило
Определение длины отрезка прямой общего положения и
углов наклона прямой к плоскостям проекций
Следует построить прямоугольный треугольник, одним катетом которого является горизонтальная (фронтальная) проекция отрезка, другим катетом - абсолютная величина алгебраической разности аппликат (ординат) концов отрезка. Гипотенуза будет равна длине отрезка, а угол между гипотенузой и катетом, равным горизонтальной (фронтальной) проекции отрезка, равен углу наклона отрезка к горизонтальной (фронтальной) плоскости проекций.