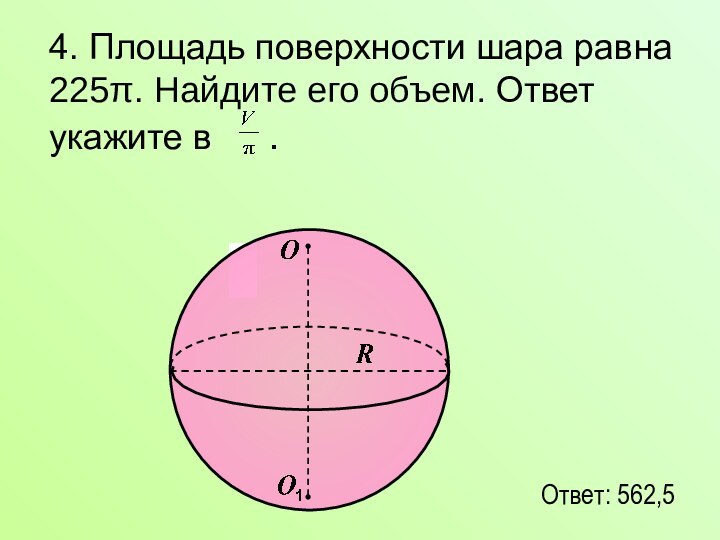
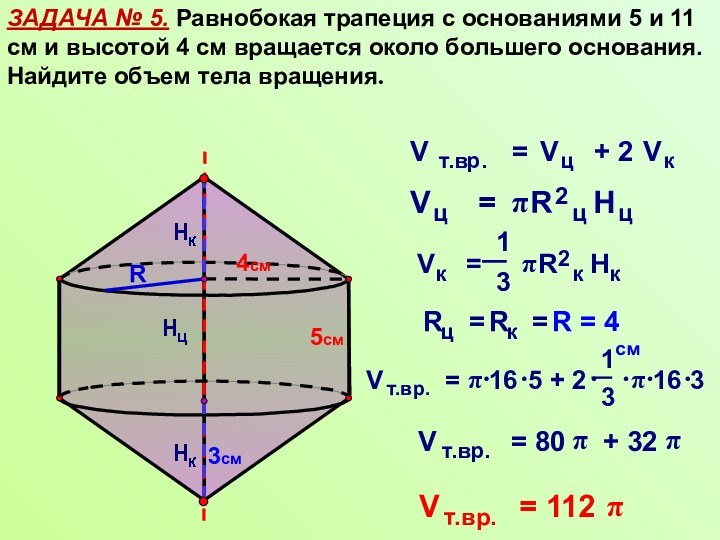
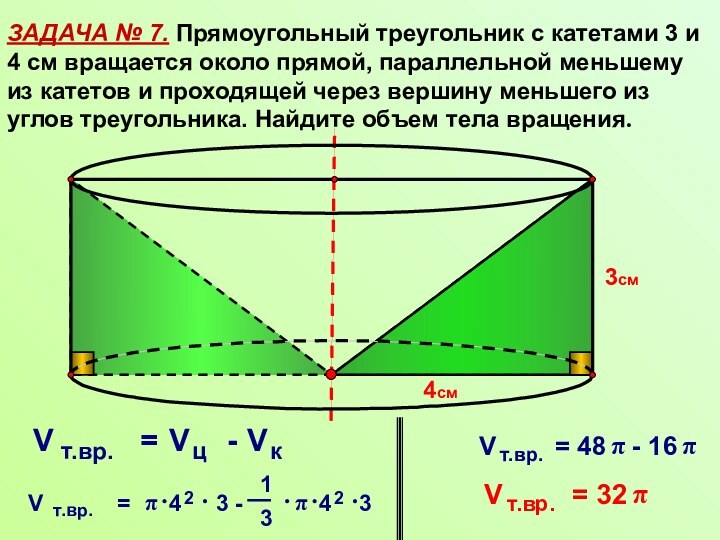
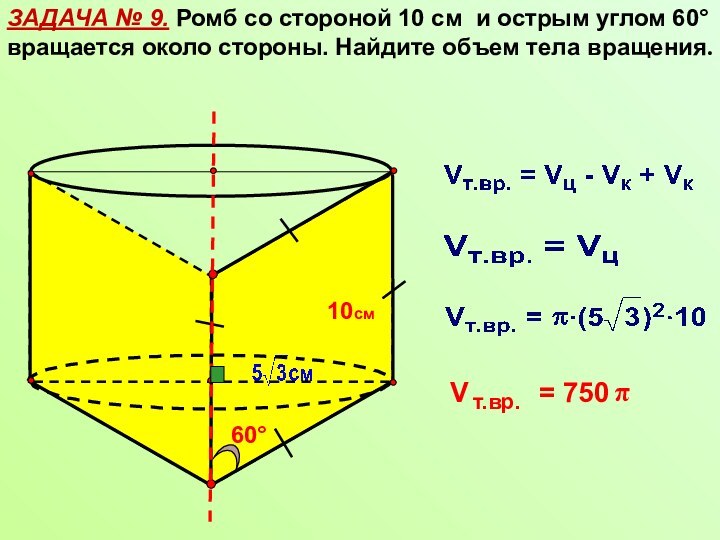
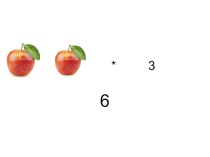
задач практического и прикладного характера.
Задачи
урока.Образовательные:
- сформировать умения решать задачи на вычисление объема тел вращения и их частей;
- создать условия для контроля и самоконтроля усвоения знаний;
- осуществить выход на творческий уровень в ходе решения прикладных задач;
Развивающие:
-развивать познавательный интерес учащихся в процессе решения задач повышенной сложности и умения преодолевать трудности при их решении.
-развивать любознательность, познавательный интерес, мышление и речь, внимание и память.
Воспитательные:
- воспитывать волю и настойчивость в достижении цели.
-формировать интерес к математике и ее приложениям.