Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Некоторые часто встречающиеся дискретные распределения

Содержание

2. Стрелок производит 3 выстрела по мишени. Вероятность
3. Найдем MX и DX для биномиального распределенияВведем
4. Тогда математическое ожидание случайной величины Х:MX=MZ1+MZ2+…+MZnНайдем математическое
5. Найдем дисперсию DZi
6. Так как случайные величины Zi независимы, то
7. Таким образом, для случайной величины, распределенной по биномиальному закону,
8. Распределение Пуассона Пусть Х – число наступлений
9. При работе оборудования время от времени возникают
10. =3^A2/ФАКТР(A2)*EXP(-3)
11. =3^A2/ФАКТР(A2)*EXP(-3)
13. Для распределения Пуассона MX=a, DX=a
14. Биномиальное распределение и распределение Пуассона связаны: распределение
15. ПРИМЕР. По цели производится 50 независимых выстрелов.
16. Решение:Найдем параметр a распределения Пуассона:Событие А -
17. Тогда вероятность р50(1) того, что из 50-ти выстрелов будет одно попадание по формуле Пуассона будет:
18. ГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ Проводится n независимых испытаний, в
19. ГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ Х принимает значения 1,2,3…,k,…
20. Можно показать, что :
21. Игральная кость бросается до первого появления шестерки. Х- число сделанных бросков. Найти распределение Х, MX, DXПРИМЕР.
22. Скачать презентацию
23. Похожие презентации

Стрелок производит 3 выстрела по мишени. Вероятность попадания при одном выстреле равна 0,6. Х-число попаданий. Найти распределение Х.ПРИМЕР.

Главная
Математика
Некоторые часто встречающиеся дискретные распределения

Проводится n испытаний по схеме Бернулли с вероятностью успеха p. Х-число успехов.Тогда

Стрелок производит 3 выстрела по мишени. Вероятность попадания при одном выстреле равна

Найдем MX и DX для биномиального распределенияВведем для каждого i=1,2…n случайную величину

Тогда математическое ожидание случайной величины Х:MX=MZ1+MZ2+…+MZnНайдем математическое ожидание ZiРяд распределения Zi имеет

Так как случайные величины Zi независимы, то

Таким образом, для случайной величины, распределенной по биномиальному закону,

Распределение Пуассона Пусть Х – число наступлений редкого события за некоторый промежуток

При работе оборудования время от времени возникают сбои. В среднем за месяц

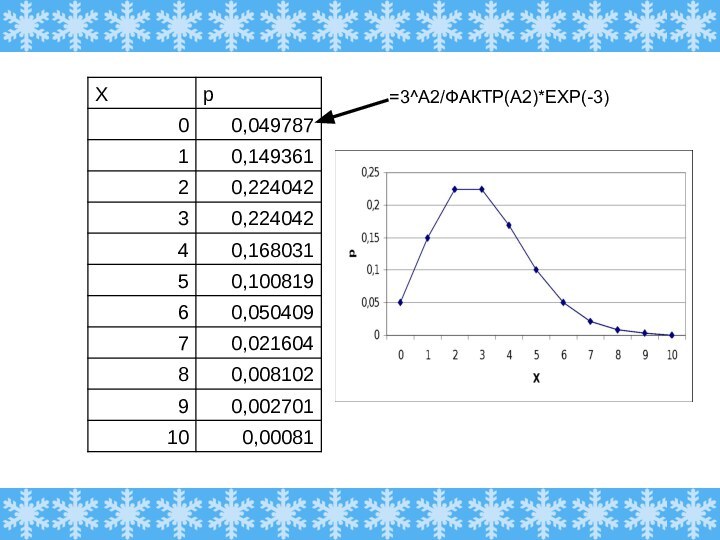
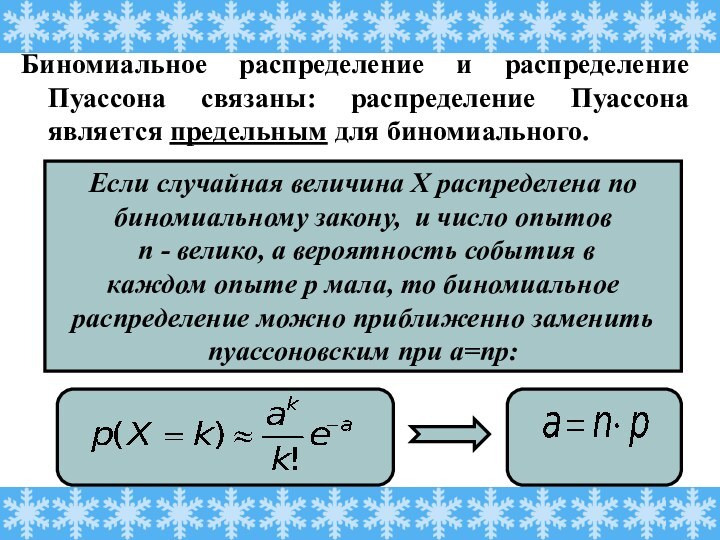
Некоторые часто встречающиеся дискретные распределения

Биномиальное распределение и распределение Пуассона связаны: распределение Пуассона является предельным для биномиального.

ПРИМЕР. По цели производится 50 независимых выстрелов. Вероятность попадания в цель при

Решение:Найдем параметр a распределения Пуассона:Событие А - попадание при одном выстреле. Вероятность

Тогда вероятность р50(1) того, что из 50-ти выстрелов будет одно попадание по формуле Пуассона будет:

ГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ Проводится n независимых испытаний, в каждом из которых возможны 2

ГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ Х принимает значения 1,2,3…,k,…

Игральная кость бросается до первого появления шестерки. Х- число сделанных бросков. Найти распределение Х, MX, DXПРИМЕР.

Слайды презентации

Слайд 2
Стрелок производит 3 выстрела по мишени. Вероятность попадания

Стрелок производит 3 выстрела по мишени. Вероятность попадания при одном выстреле

при одном выстреле равна 0,6. Х-число попаданий. Найти распределение

Х.

ПРИМЕР.

Слайд 3
Найдем MX и DX для биномиального распределения
Введем для

Найдем MX и DX для биномиального распределенияВведем для каждого i=1,2…n случайную

каждого i=1,2…n случайную величину Zi .
Тогда
Х= Z1 +Z2

+…+Zn

Слайд 4
Тогда математическое ожидание случайной величины Х:
MX=MZ1+MZ2+…+MZn
Найдем математическое ожидание

Тогда математическое ожидание случайной величины Х:MX=MZ1+MZ2+…+MZnНайдем математическое ожидание ZiРяд распределения Zi

Zi
Ряд распределения Zi имеет вид:
Тогда MZi =p и MX=np.

Слайд 5
Найдем дисперсию DZi

Слайд 6
Так как случайные величины Zi независимы, то

Слайд 7

Таким образом, для случайной величины,
распределенной по биномиальному

закону,

Слайд 8 Распределение Пуассона

Пусть Х – число наступлений редкого

Распределение Пуассона Пусть Х – число наступлений редкого события за некоторый

события за
некоторый промежуток времени.
Известно среднее число наступлений

этого
события за этот промежуток времени a
Тогда Х может принимать значения
0, 1, 2,…,k,…

Говорят, что Х имеет распределение Пуассона с параметром a.

Слайд 9 При работе оборудования время от времени
возникают сбои.

При работе оборудования время от времени возникают сбои. В среднем за

В среднем за месяц возникает
3 сбоя. Пусть Х-число

сбоев за месяц. Найти
распределение Х.
Вычислить вероятности событий:
А - за месяц будет не больше 2-х сбоев;
В - в течение месяца произойдет хотя бы один
сбой.

ПРИМЕР.

Слайд 10 =3^A2/ФАКТР(A2)*EXP(-3)

Слайд 11 =3^A2/ФАКТР(A2)*EXP(-3)

Слайд 12

Слайд 13 Для распределения Пуассона MX=a, DX=a

Слайд 14
Биномиальное распределение и распределение Пуассона связаны: распределение Пуассона

Биномиальное распределение и распределение Пуассона связаны: распределение Пуассона является предельным для

является предельным для биномиального.

Если случайная величина Х распределена

по
биномиальному закону, и число опытов
n - велико, а вероятность события в
каждом опыте р мала, то биномиальное
распределение можно приближенно заменить
пуассоновским при a=np:

Слайд 15 ПРИМЕР.
По цели производится 50 независимых
выстрелов. Вероятность

ПРИМЕР. По цели производится 50 независимых выстрелов. Вероятность попадания в цель

попадания в цель
при одном выстреле равна 0.04.
Используя

предельное свойство
биномиального распределения, найти
вероятность того, что в цель попадет
один снаряд.

Слайд 16 Решение:
Найдем параметр a распределения Пуассона:
Событие А - попадание

Решение:Найдем параметр a распределения Пуассона:Событие А - попадание при одном выстреле.

при одном выстреле.
Вероятность р(А)=0.04. Всего производится серия таких

выстрелов: n=50.
Так как р достаточно мало, а n - велико, биномиальное распределение приближенно можно заменить распределением Пуассона.

Слайд 17 Тогда вероятность р50(1) того, что из 50-ти выстрелов

будет одно попадание по формуле Пуассона будет:

Слайд 18
ГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ
Проводится n независимых испытаний,
в каждом

ГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ Проводится n независимых испытаний, в каждом из которых возможны

из которых возможны 2 исхода: успех
с вероятностью p

и неудача с вероятностью 1-p.
Испытания проводятся до первого успеха. Пусть X –
число проведенных испытаний. Тогда X имеет
геометрическое распределение.