- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Неопределенный интеграл: свойства и методы интегрирования
Содержание
- 2. История возникновения интегралаНеопределенный интеграл. Методы интегрированияСвойства неопределенного интегралаТабличные интегралыТест по теме : «Вычисление неопределенного интеграла»
- 3. История возникновения интеграла Интегрирование прослеживается
- 4. Следующий крупный шаг в исчисление
- 5. Следующий значительный прогресс в исчислении интегралов появится
- 6. Неопределенным интегралом называется функция F(x) + C,
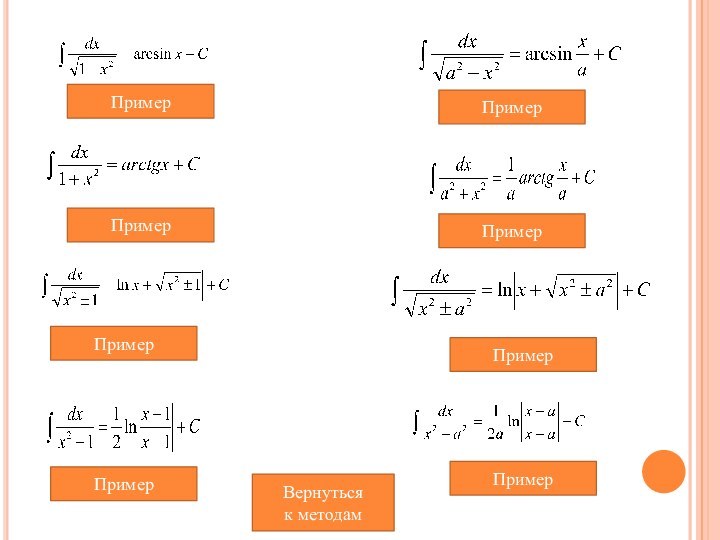
- 7. ПримерПримерПримерПримерПримерПримерПримерПримерТабличные интегралыдалее
- 8. ПримерПримерПримерПримерПримерПримерПримерПримерВернуться к методам
- 9. Свойства интегралаЗам.1. чтобы войти в поддифференциал необходимо от функции взять первообразную В НАЧАЛО
- 10. вернуться к табличным интегралам
- 11. вернуться к табличным интегралам
- 12. вернуться к табличным интегралам
- 13. вернуться к табличным интегралам
- 14. вернуться к табличным интегралам
- 15. вернуться к табличным интегралам
- 16. вернуться к табличным интегралам
- 17. вернуться к табличным интегралам
- 18. вернуться к табличным интегралам
- 19. вернуться к табличным интегралам
- 20. вернуться к табличным интегралам
- 21. вернуться к табличным интегралам
- 22. вернуться к табличным интегралам
- 23. вернуться к табличным интегралам
- 24. вернуться к табличным интегралам
- 25. вернуться к табличным интегралам
- 28. Скачать презентацию
- 29. Похожие презентации
История возникновения интегралаНеопределенный интеграл. Методы интегрированияСвойства неопределенного интегралаТабличные интегралыТест по теме : «Вычисление неопределенного интеграла»









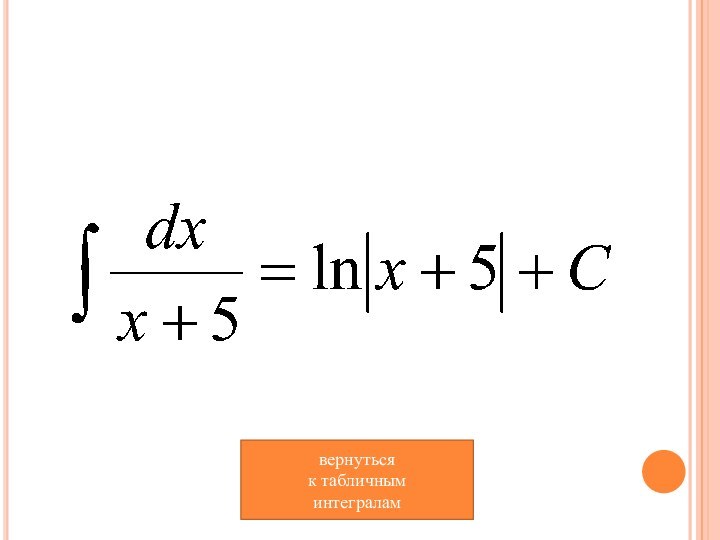
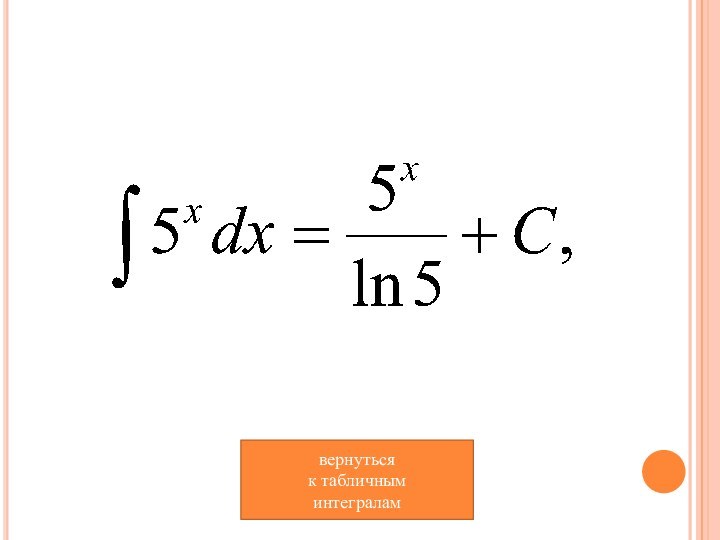
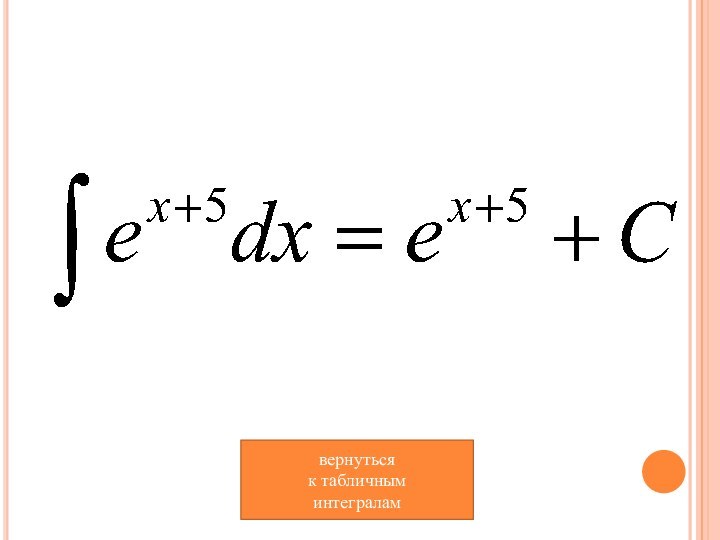
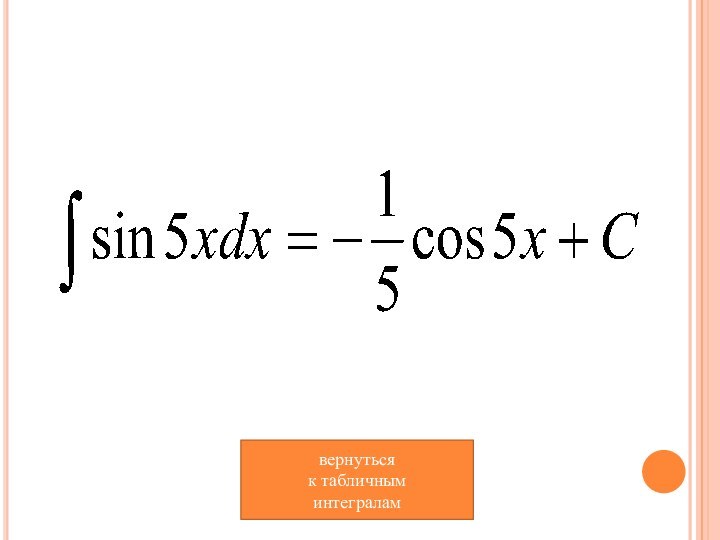
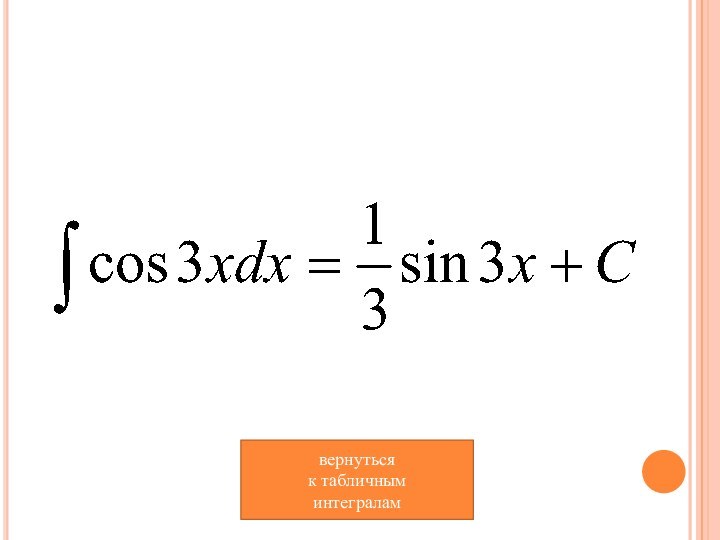
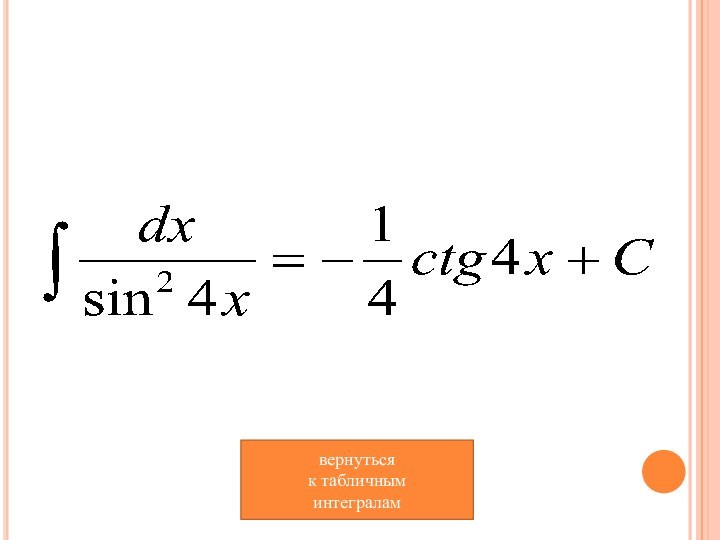
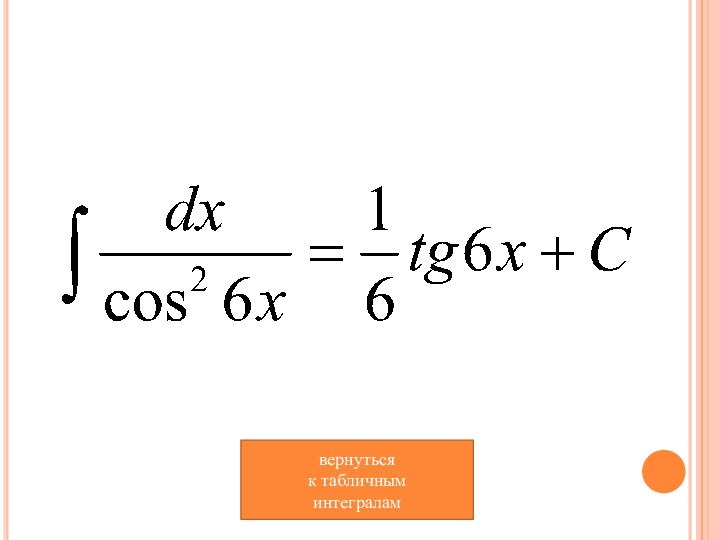
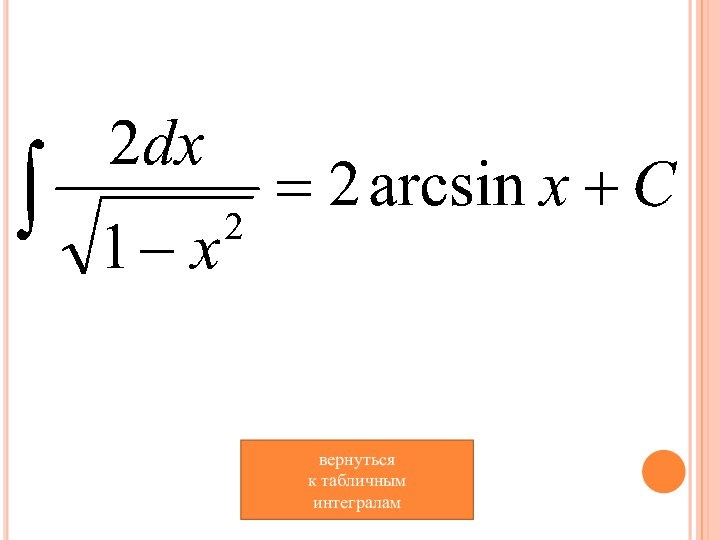

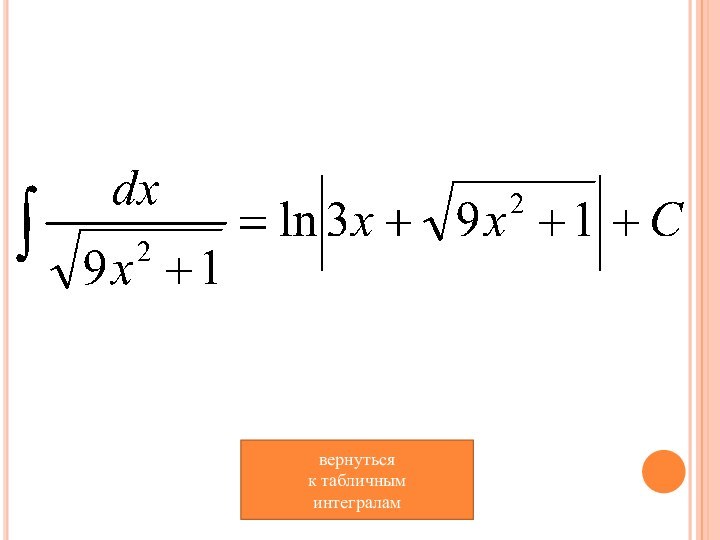
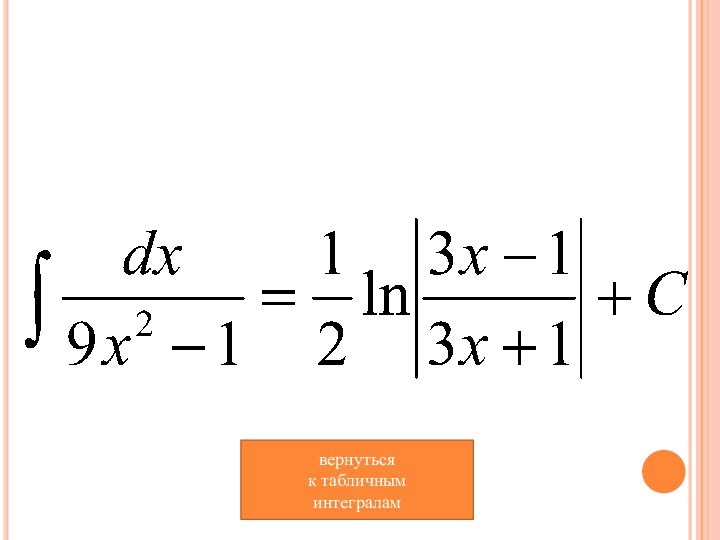

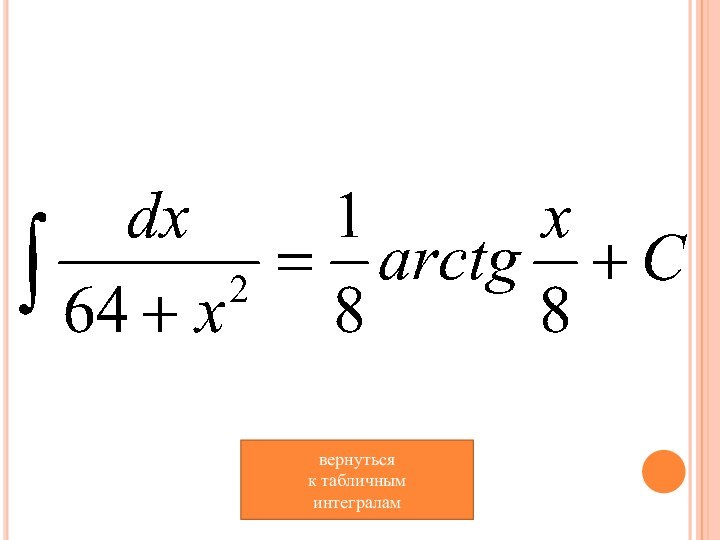
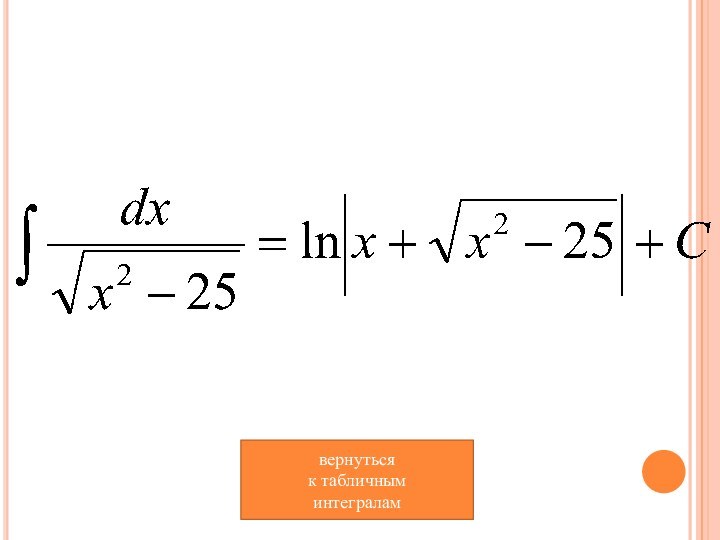

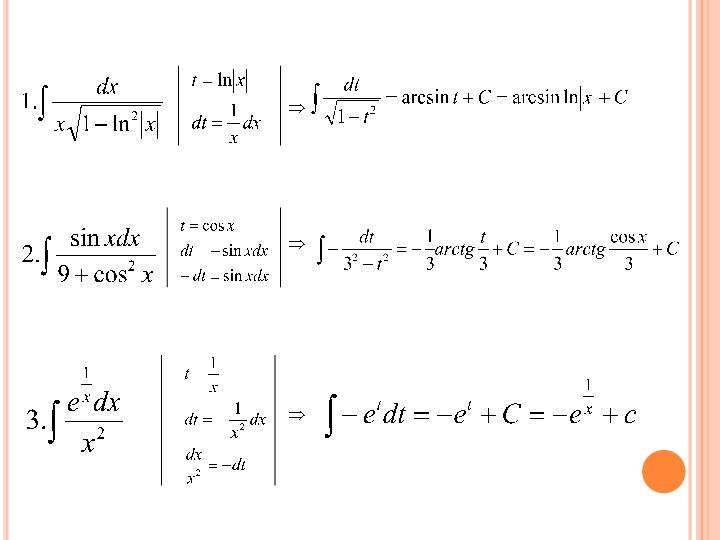


Слайд 2
История возникновения интеграла
Неопределенный интеграл. Методы интегрирования
Свойства неопределенного интеграла
Табличные
интегралы
Слайд 3
История возникновения интеграла
Интегрирование прослеживается ещё
в древнем Египте, примерно в 1800 г. до н.
э., Московский математический папирус демонстрирует знание формулы объёма усечённой пирамиды. Первым известным методом для расчёта интегралов является метод исчерпывания Евдокса (примерно 370 до н. э.), который пытался найти площади и объёмы, разрывая их на бесконечное множество частей, для которых площадь или объём уже известны. Этот метод был подхвачен и развит Архимедом, и использовался для расчёта площадей парабол и приближенного расчёта площади круга. Аналогичные методы были разработаны независимо в Китае в 3-м веке н. э. Лю Хуэйем, который использовал их для нахождения площади круга. Этот метод был впоследствии использован Дзю Чонгши для нахождения объёма шара.далее
Слайд 4 Следующий крупный шаг в исчисление интегралов
был сделан в Ираке, в XI веке, математиком Ибн
ал-Хайсамом (известным как Alhazen в Европе), в своей работе «Об измерении параболического тела» он приходит к уравнению четвёртой степени. Решая эту проблему, он проводит вычисления, равносильные вычислению определённого интеграла, чтобы найти объём параболоида. Используя математическую индукцию, он смог обобщить свои результаты для интегралов от многочленов до четвёртой степени. Таким образом, он был близок к поиску общей формулы для интегралов от полиномов, но он не касается любых многочленов выше четвёртой степени.далее
Слайд 5
Следующий значительный прогресс в исчислении интегралов появится лишь
в XVI веке. В работах Кавальери с его методом
неделимых, а также в работах Ферма, были заложены основы современного интегрального исчисления. Дальнейшие шаги были сделаны в начале XVII века Барроу и Торричелли, которые представили первые намеки на связь между интегрированием и дифференцированием.
Слайд 6
Неопределенным интегралом называется функция F(x) + C,
содержащая
произвольное постоянное C, дифференциал
которой равен подынтегральному выражению f(x)dx, т.е.
или
1. Непосредственный, т.е. по таблице
2. Метод замены переменных или внесения под знак дифференциала
3. По частям
Понятие неопределенного интеграла
Методы интегрирования