Слайд 2
First, a Word About Hammers
requirements for this to
be a good idea
a way of transforming problems into
nails (MLCPs)
a hammer (Lemke’s algorithm)
lots of advanced info + one hour = something has to give
majority of lecture is motivating you to care about the hammer by showing you how useful nails can be
make you hunger for more info post-lecture
very little on how the hammer works in this hour
“If the only tool you have is a hammer, you tend to see every problem as a nail.”
Abraham Maslow
Слайд 3
Hammers (cont.)
by definition, not the optimal way to
solve problems, BUT
computers are very fast these days
often don’t
care about optimality
prepro, prototypes, tools, not a profile hotspot, etc.
can always move to optimal solution after you verify it’s a problem you actually want to solve
Слайд 4
What are “advanced game math problems”?
problems that are
ammenable to mathematical modeling
state the problem clearly
state the desired
solution clearly
describe the problem with equations so a proposed solution’s quality is measurable
figure out how to solve the equations
why not hack it?
I believe better modeling is the future of game technology development (consistency, not reality)
Слайд 5
Prerequisites
linear algebra
vector, matrix symbol manipulation at least
calculus concepts
what
derivatives mean
comfortable with math notation and concepts
Слайд 6
Overview of Lecture
random assortment of example problems breifly
mentioned
5 specific example problems in some depth
including one that
I ran into recently and how I solved it
generalize the example models
transform them all to MLCPs
solve MLCPs with Lemke’s algorithm
Слайд 7
A Look Forward
linear equations
Ax = b
linear inequalities
Ax
>= b
linear programming
min cTx
s.t. Ax >= b, etc.
quadratic programming
min
½ xTQx + cTx
s.t. Ax >= b
Dx = e
linear complimentarity problem
a = Af + b
a >= 0, f >= 0
aifi = 0
Слайд 8
Applications to Games
graphics, physics, ai, even ui
computational geometry
visibility
contact
curve
fitting
constraints
integration
graph theory
network flow
economics
site allocation
game theory
IK
machine learning
image processing
Слайд 9
Applications to Games (cont.)
don’t forget...
The Elastohydrodynamic Lubrication Problem
Solving
Optimal Ownership Structures
“The two parties establish a relationship in
which they exchange feed ingredients, q, and manure, m.”
Слайд 10
Specific Examples #1a:
Ease Cubic Fitting
warm up with
an ease curve cubic
x(t)=at3+bt2+ct+d
x’(t)=3at2+2bt+c
4 unknowns a,b,c,d (DOFs) we get
to set, we choose:
x(0) = 0, x(1) = 1
x’(0) = 0, x’(1) = 0
1
x
t
0
0
1
Слайд 11
Specific Examples #1a:
Ease Cubic Fitting (cont.)
x(t)=at3+bt2+ct+d,
x’(t)=3at2+2bt+c
x(0) = a03+b02+c0+d = d =
0
x(1) = a13+b12+c1+d = a+b+c+d = 1
x’(0) = 3a02+2b0+c = c = 0
x’(1) = 3a12+2b1+c = 3a + 2b + c = 0
Слайд 12
Specific Examples #1a:
Ease Cubic Fitting (cont.)
d
= 0, a+b+c+d = 1, c = 0, 3a
+ 2b + c = 0
a+b=1, 3a+2b=0
a=1-b => 3(1-b)+2b = 3-3b+2b = 3-b = 0
b=3, a=-2
x(t) = 3t2 - 2t3
Слайд 13
Specific Examples #1a:
Ease Cubic Fitting (cont.)
or,
x(0)
=
d = 0
x(1) = a + b + c + d = 1
x’(0) = c = 0
x’(1) = 3a + 2b + c = 0
0 0 0 1
1 1 1 1
0 0 1 0
3 2 1 0
x(0)
x(1)
x’(0)
x’(1)
a
b
c
d
0
1
0
0
=
=
Ax = b, a system of linear equations
(can solve for any rhs)
Слайд 14
Specific Examples #1b:
Cubic Spline Fitting
same technique to
fit higher order polynomials, but they “wiggle”
piecewise cubic is
better
“natural cubic spline”
xi(ti)=xi xi(ti+1)=xi+1
x’i(ti) - x’i-1(ti) = 0
x’’i(ti) - x’’i-1(ti) = 0
there is coupling between the splines, must solve simultaneously
x0
x1
x2
x3
t0
t1
t2
t3
4 DOF per spline
2 endpoint eqns per spline
4 derivative eqns for inside points
2 missing eqns = endpoint slopes
Слайд 15
Specific Examples #1b:
Cubic Spline Fitting (cont.)
a0
b0
c0
d0
a1
b1
c1
d1
.
.
.
x0
x1
0
0
x1
x2
0
0
.
.
.
=
xi(ti)=xi
xi(ti+1)=xi+1
x’i(ti) - x’i-1(ti) = 0
x’’i(ti) - x’’i-1(ti)
= 0
.
.
.
Ax = b, a system of
linear equations
Слайд 16
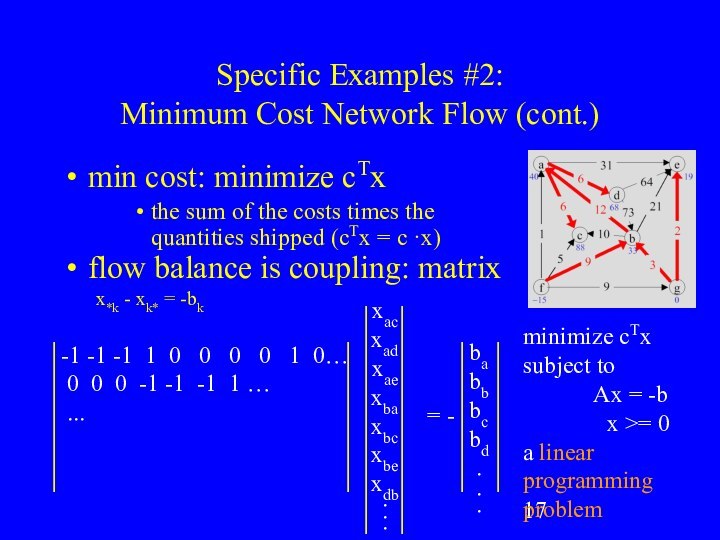
Specific Examples #2:
Minimum Cost Network Flow
what is
the cheapest flow route(s) from sources to sinks?
model, want
to minimize cost
cij = cost of i to j arc
bi = i’s supply/demand, sum(bi)=0
xij = quantity shipped on i to j arc
x*k = sum(xik) = flow into k
xk* = sum(xki) = flow out of k
flow balance: x*k - xk* = -bk
one-way streets: xij >= 0
Слайд 17
Specific Examples #2:
Minimum Cost Network Flow (cont.)
min
cost: minimize cTx
the sum of the costs times the
quantities shipped (cTx = c ·x)
flow balance is coupling: matrix
x*k - xk* = -bk
xac
xad
xae
xba
xbc
xbe
xdb
.
.
.
= -
-1 -1 -1 1 0 0 0 0 1 0…
0 0 0 -1 -1 -1 1 …
...
ba
bb
bc
bd
.
.
.
minimize cTx
subject to
Ax = -b
x >= 0
a linear programming problem
Слайд 18
Specific Examples #3:
Points in Polys
point in convex
poly defined by planes
n1 · x >= d1
n2 ·
x >= d2
n3 · x >= d3
farthest point in a direction in poly, c:
n1
n2
n3
x
Ax >= b,
linear inequality
min -cTx
s.t. Ax >= b
linear programming
Слайд 19
Specific Examples #3:
Points in Polys (cont.)
closest point
in two polys
min (x2-x1)2
s.t. A1x1 >= b1
A2x2 >= b2
stack ‘em in blocks, Ax >= b
n1
n2
x1
n3
x2
x1
x2
x =
A1 A2
A =
what about (x2-x1)2, how do we stack it?
b1
b2
b =
Слайд 20
Specific Examples #3:
Points in Polys (cont.)
how do
we stack x1,x2 into single x given
(x2-x1)2 = x22-2x2•x1+x12
x1
x2
x1T x2T
1 -1
-1 1
= x22-2x2 • x1+x12 = xTQx
min xTQx
s.t. Ax >= b
a quadratic programming problem
x2 = xTx = x · x
1 = identity matrix
Слайд 21
Specific Examples #3:
Points in Polys (cont.)
more points,
more polys!
min (x2-x1)2 + (x3-x2)2 + (x3-x1)2
x1
x2
x3
x1T x2T x3T
2 -1 -1
-1 2 -1
-1 -1 2
min xTQx
s.t. Ax >= b
another quadratic programming problem
same form for all these poly problems
never specified 2d, 3d, 4d, nd!
= xTQx
Слайд 22
Specific Examples #4:
Contact
model like IK constraints
a =
Af + b
a >= 0, no penetrating
f >= 0,
no pulling
aifi = 0, complementarity
(can’t push if leaving)
f1
f2
a1
a2
f1
f2
a1
a2
linear complementarity problem
it’s a mixed LCP if some ai = 0, fi free, like for equality constraints
Слайд 23
Specific Examples #5:
Joint Limits in CCD IK
how
to do child-child constraints in CCD?
parent-child are easy, but
need a way to couple two children to limit them relative to each other
how to model this & handle all the cases?
define dn= gn - an
min (x1 - d1)2 + (x2 - d2)2
s.t. c1min <= a1+x1 - a2-x2 <= c1max
parent-child are easy in this framework: c2min <= a1+x1 <= c2max
another quadratic program:
min xTQx
s.t. Ax >= b
a1
g1
a2
g2
a1
g1
Слайд 24
What Unifies These Examples?
linear equations
Ax = b
linear
inequalities
Ax >= b
linear programming
min cTx
s.t. Ax >= b, etc.
quadratic
programming
min ½ xTQx + cTx
s.t. Ax >= b
Dx = e
linear complimentarity problem
a = Af + b
a >= 0, f >= 0
aifi = 0
Слайд 25
QP is a Superset of Most
quadratic programming
min ½xTQx
+ cTx
s.t. Ax >= b
Dx
= e
linear equations
Ax = b
Q, c, A, b = 0
linear inequalities
Ax >= b
Q, c, D, e = 0
linear programming
min cTx
s.t. Ax >= b, etc.
Q, etc. = 0
but MLCP is a superset of convex QP!
Слайд 26
Karush-Kuhn-Tucker Optimality Conditions get us to MLCP
for QP
form
“Lagrangian”
L(x,u,v) = ½ xTQx + cTx - uT(Ax -
b) - vT(Dx - e)
for optimality (if convex):
∂L/ ∂x = 0
Ax - b >= 0
Dx - e = 0
u >= 0 ui(Ax-b)i = 0
this is related to basic calculus min/max f’(x) = 0 solve
min ½ xTQx + cTx
s.t. Ax - b >= 0
Dx - e = 0
Слайд 27
Karush-Kuhn-Tucker Optimality Conditions (cont.)
L(x,u,v) = ½ xTQx +
cTx - uT(Ax - b) - vT(Dx - e)
y = ∂L/ ∂x = Qx + c - ATu - DTv = 0, x free
w = Ax - b >= 0, u >= 0, wiui = 0
s = Dx - e = 0, v free
x
v
u
Q -DT -AT
D 0 0
A 0 0
=
y
s
w
+
c
-e
-b
y, s = 0
x, v free
w, u >= 0
wiui = 0
Слайд 28
This is an MLCP
x
v
u
Q -DT -AT
D
0 0
A 0
0
=
y
s
w
+
c
-e
-b
y, s = 0
x, v free
w, u >= 0
wiui = 0
a
=
A
f
b
+
aifi = 0
some a >= 0, some = 0
some f >= 0, some free
(but they correspond so complementarity holds)
Слайд 29
Modeling Summary
a lot of interesting problems can be
formulated as MLCPs
model the problem mathematically
transform it to an
MLCP
on paper or in code with wrappers
but what about solving MLCPs?
Слайд 30
Solving MLCPs
(where I hope I made you hungry
enough for homework)
Lemke’s Algorithm is only about 2x as
complicated as Gaussian Elimination
Lemke will solve LCPs, which some of these problems transform into
then, doing an “advanced start” to handle the free variables gives you an MLCP solver, which is just a bit more code over plain Lemke’s Algorithm
Слайд 31
Playing Around With MLCPs
PATH, a MCP solver (superset
of MLCP!)
really stoked professional solver
free version for “small” problems
matlab
or C
OMatrix (Matlab clone) free trial (omatrix.com)
only LCPs, but Lemke source is in trial
not a great version, but it’s really small (two pages of code) and quite useful for learning, with debug output
good place to test out “advanced starts”
my Lemke’s + advanced start code
not great, but I’m happy to share it
it’s in Objective Caml :)
Слайд 32
References for Lemke, etc.
free pdf book by Katta
Murty on LCPs, etc.
free pdf book by Vanderbei on
LPs
The LCP, Cottle, Pang, Stone
Practical Optimization, Fletcher
web has tons of material, papers, complete books, etc.
email to authors
relatively new math means authors are still alive, bonus!
Слайд 34
Specific Examples #5:
Constraints for IK
compute “forces” to
keep bones together
a1 = A11 f1 + b1
a1 :
relative acceleration
at constraint
f1 : force at constraint
b1 : external forces converted to
accelerations at constraints
A11 : force/acceleration relation matrix
f1
fe