- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Непрерывно-детерминированные, дискретнодетерминированные, дискретно-вероятностные и непрерывно-вероятностные модели
Содержание
- 2. Как
- 4. Непрерывно-детерминированные, дискретно-детерминированные, дискретно-вероятностные и непрерывно-вероятностные модели. Вебинар № 5Непрерывные модели.Дискретные модели.Стохастические модели
- 6. Будем предполагать, что возможно, хотя бы в
- 7. Пусть М=М(X,Y,Z), где X – множество входов,
- 8. Непрерывность и дискретность. Все те объекты, переменные
- 9. Свойство непрерывности и дискретности выражается в структуре
- 10. Непрерывные математические модели и методы их формирования
- 11. На рис. оказаны преобразования непрерывных ММ в
- 13. Дискретные математические модели.
- 15. Пример 2. Построение стохастической ММСС с применением аппарата СМО
- 18. СТОХАСТИЧЕСКАЯ МОДЕЛЬ [stochastic model] — такая экономико-математическая
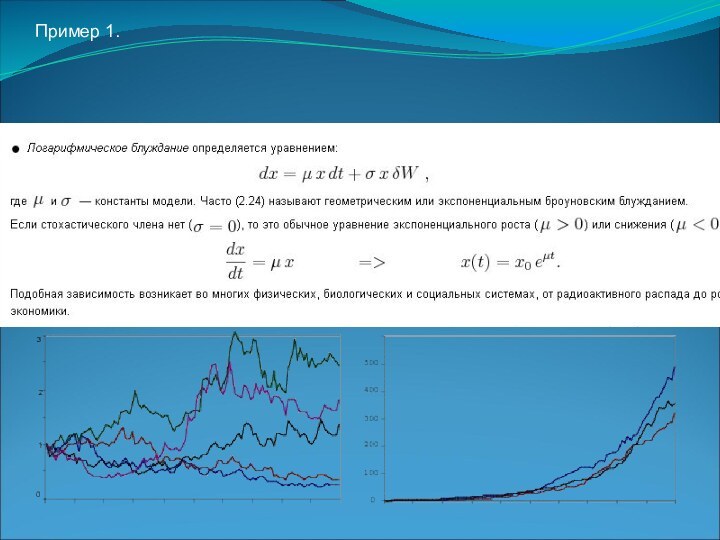
- 19. Пример 1.
- 20. Автор: Орлова И.В., Половников В.А. Издательство: Вузовский
- 21. Скачать презентацию
- 22. Похожие презентации
Как известно, величины могут быть двух типов — дискретные, т. е. принимающие «оторванные» друг от друга значения, допускающие естественную нумерацию, и непрерывные, принимающие все значения из некоторого интервала. Возможен также
















![Непрерывно-детерминированные, дискретнодетерминированные, дискретно-вероятностные и непрерывно-вероятностные модели СТОХАСТИЧЕСКАЯ МОДЕЛЬ [stochastic model] — такая экономико-математическая модель, в которой параметры, условия](/img/tmb/15/1469576/a5c7a0e36265dc45292887b56e138fee-720x.jpg)

![Непрерывно-детерминированные, дискретнодетерминированные, дискретно-вероятностные и непрерывно-вероятностные модели Анфилатов, В. С. Системный анализ в управлении [Текст]: учеб.пособие / В. С.](/img/tmb/15/1469576/60d057bdeba745a0975ab832fd087f8c-720x.jpg)
Слайд 4
Непрерывно-детерминированные, дискретно-детерминированные, дискретно-вероятностные и непрерывно-вероятностные модели.
Вебинар №
5
Непрерывные модели.
Дискретные модели.
Стохастические модели
Слайд 5
Модели — как содержательные, так и математические — могут
быть либо дискретными, либо непрерывными, либо смешанными. Между этими типами нет принципиального барьера и при уточнении или видоизменении модели дискретная картина может стать непрерывной и обратно; то же может произойти в процессе решения математической задачи.Таким образом, во многих задачах при составлении математической модели, а также при выборе метода ее исследования надо учитывать возможность применения как «дискретного», так и «непрерывного» аппаратов (например, для дискретных моделей характерно применение сумм, а для непрерывных — производных и интегралов) независимо от характера исходной картины.
Слайд 6 Будем предполагать, что возможно, хотя бы в принципе,
установить и на некотором языке описания (например, средствами математики)
охарактеризовать зависимость каждой из выходных переменных от входных. Связь между входными и выходными переменными моделируемого объекта в принципе может характеризоваться графически, аналитически, т.е. посредством некоторой формулы общего вида, или алгоритмически. Независимо от формы представления конструкта, описывающего эту связь, будем именовать его оператором вход-выход и обозначать через В.Слайд 7 Пусть М=М(X,Y,Z), где X – множество входов, Y
– выходов, Z – состояний системы. Схематически можно это
изобразить: X Z Y.Рассмотрим теперь наиболее существенные с точки зрения моделирования внутренние свойства объектов разного класса. При этом придется использовать понятие структура и параметры моделируемого объекта. Под структурой понимается совокупность учитываемых в модели компонентов и связей, содержащихся внутри объекта, а после формализации описания объекта – вид математического выражения, которое связывает его входные и выходные переменные (например: у=au+bv). Параметры представляют собой количественные характеристики внутренних свойств объекта, которые отражаются принятой структурой, а в формализованной математической модели они суть коэффициенты (постоянные переменные), входящие в выражения, которыми описывается структура (а и b).
Слайд 8 Непрерывность и дискретность. Все те объекты, переменные которых
(включая, при необходимости, время) могут принимать несчетное множество сколь
угодно близких друг к другу значений называются непрерывными или континуальными. Подавляющее большинство реальных физических и теоретических объектов, состояние которых характеризуется только макроскопическими физическими величинами (температура, давление, скорость, ускорение, сила тока, напряженность электрического или магнитного полей и т.д.) обладают свойством непрерывности. Математические структуры, адекватно описывающие такие объекты, тоже должны быть непрерывными. Поэтому при модельном описании таких объектов используется главным образом, аппарат дифференциальных и интегро-дифференциальных уравнений. Объекты, переменные которых могут принимать некоторое, практически всегда конечное число наперед известных значений, называются дискретными. Примеры: релейно-контактные переключательные схемы, коммутационные системы АТС. Основой формализованного описания дискретных объектов является аппарат математической логики (логические функции, аппарат булевой алгебры, алгоритмические языки). В связи с развитием ЭВМ дискретные методы анализа получили широкое распространение также для описания и исследования непрерывных объектов.Слайд 9 Свойство непрерывности и дискретности выражается в структуре множеств
(совокупностей), которым принадлежат параметры состояния, параметр процесса и входы,
выходы системы. Таким образом, дискретность множеств Z, Т, Х, Y ведет к модели, называемой дискретной, а их непрерывность — к модели с непрерывными свойствами. Дискретность входов (импульсы внешних сил, ступенчатость воздействий и др.) в общем случае не ведет к дискретности модели в целом. Важной характеристикой дискретной модели является конечность или бесконечность числа состояний системы и числа значений выходных характеристик. В первом случае модель называется дискретной конечной. Дискретность модели также может быть как естественным условием (система скачкообразно меняет свое состояние и выходные свойства), так и искусственно внесенной особенностью. Типичный пример последнего – замена непрерывной математической функции на набор ее значений в фиксированных точках.
Слайд 10
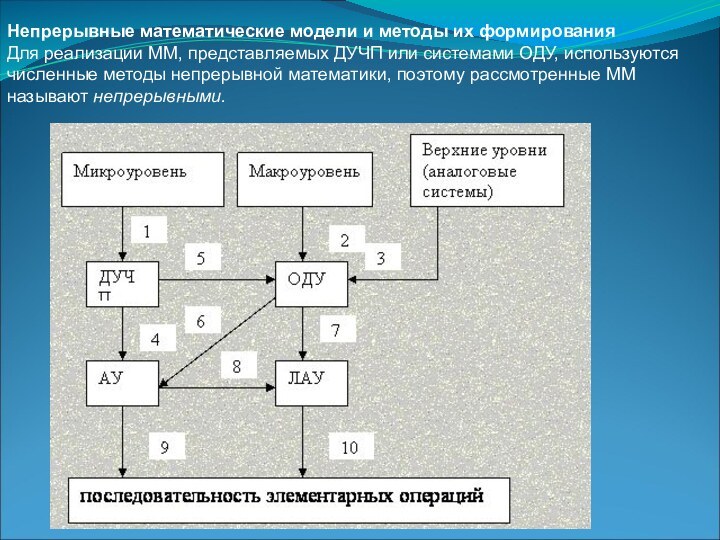
Непрерывные математические модели и методы их формирования
Для
реализации ММ, представляемых ДУЧП или системами ОДУ, используются численные
методы непрерывной математики, поэтому рассмотренные ММ называют непрерывными.Слайд 11 На рис. оказаны преобразования непрерывных ММ в процессе
перехода от исходных формулировок задач к рабочим программам, представляющим
собой последовательности элементарных арифметических и логических операций. Стрелками 1, 2 и 3 показаны переходы от описания структуры объектов на соответствующем иерархическом уровне к математической формулировке задачи. Дискретизация (4) и алгебраизация (5) ДУЧП по пространственным переменным осуществляются методами конечных разностей (МКР) или конечных элементов (МКЭ). Применение МКР или МКЭ к стационарным ДУЧП приводит к системе алгебраических уравнений (АУ), а к нестационарным ДУЧП—к системе ОДУ. Алгебраизация и дискретизация системы ОДУ по переменной t осуществляются методами численного интегрирования. Для нелинейных ОДУ (6) это преобразование приводит к системе нелинейных АУ, для линейных ОДУ (7) — к системе линейных алгебраических уравнений (ЛАУ). Нелинейные АУ решаются итерационными методами. Стрелка 8 соответствует решению методом Ньютона, основанному на линеаризации уравнений, стрелка 9—методами Зейделя, Якоби, простой итерации и т. п. Решение системы ЛАУ сводится к последовательности элементарных операций (10) с помощью методов Гаусса или LU-разложения.Слайд 12
Непрерывные ММ и используемые для их
анализа методы вычислительной математики получили широкое распространение в САПР различных отраслей промышленности.Создание методики автоматического формирования математических моделей систем позволило автоматизировать процедуры анализа и верификации широкого класса технических объектов. Инвариантный характер этой методики обусловил разработку на ее основе методов и алгоритмов, реализованных во многих ПМК проектирования электронных, механических, гидравлических, теплоэнергетических устройств и систем. Известны такие методы формирования ММ как узловой метод, контурный метод, метод переменных состояния.
Слайд 13
Дискретные математические модели.
Дискретной математической моделью
называется модель, в которой выполнена дискретизация тех или иных переменных. Рассмотрим ММ, в которых дискретными являются зависимые переменные, характеризующие состояние моделируемого объекта.Проектирование систем на функционально-логическом и системном уровнях основано на применении дискретных ММ. При моделировании в подсистемах функционально-логического проектирования принимаются те же допущения, что и при моделировании аналоговых систем на верхних уровнях. Кроме того, моделируемый объект представляется совокупностью взаимосвязанных логических элементов, состояния которых характеризуются переменными, принимающими значения в конечном множестве. В простейшем случае это множество {0, 1}. Непрерывное время t заменяется дискретной последовательностью моментов времени tк, при этом длительность такта .
Следовательно, математической моделью объекта является конечный автомат (КА). Функционирование КА описывается системой логических уравнений КА
Слайд 14
На системном уровне проектирования систем преимущественно распространены модели
систем массового обслуживания (СМО). Для таких моделей характерно то, что в них отображаются объекты двух типов—заявки на обслуживание и обслуживающие аппараты (ОА). При проектировании ВС заявками являются решаемые задачи, а обслуживающими аппаратами—оборудование ВС. Заявка может находиться в состоянии «обслуживание» или «ожидание», а обслуживающий аппарат—в состоянии «свободен» или «занят». Состояние СМО характеризуется состояниями ее ОА и заявок. Смена состояний называется событием. Модели СМО используются для исследования процессов, происходящих в этой системе при подаче на входы потоков заявок. Эти процессы представляются последовательностями событий. По результатам исследования определяются наиболее важные выходные параметры системы: производительность, пропускная способность, вероятность и среднее время решения задач, коэффициенты загрузки оборудования.Слайд 16
Появление параллельных и конвейерных систем, необходимость моделировать
процессы функционирования не только аппаратных, но и программных средств привело к появлению класса дискретных ММ, называемых сетями Петри. Сети Петри можно использовать для моделирования на функционально-логическом и системном уровнях проектирования широкого круга систем и сетей.Сети Петри и СМО широко используются для описания функционирования производственных участков, линий и цехов, ориентированных на многономенклатурное производство изделий. Сети Петри — эффективный инструмент разработки самих САПР. Эти сети могут служить моделями алгоритмов функционирования различных устройств дискретной автоматики.
Слайд 17
В комбинированных дискретно-непрерывных моделях независимые переменные могут
изменяться как дискретно, так и непрерывно. В рамках методологии комбинированного моделирования исследуемая система описывается с помощью элементов, их атрибутов и переменных состояния. Поведение системы имитируется путем вычисления значений переменных состояния через небольшие отрезки времени и значений атрибутов элементов в моменты свершения событий.Слайд 18 СТОХАСТИЧЕСКАЯ МОДЕЛЬ [stochastic model] — такая экономико-математическая модель,
в которой параметры, условия функционирования и характеристики состояния моделируемого
объекта представлены случайными величинами и связаны стохастическими (т. е. случайными, нерегулярными) зависимостями, либо исходная информация также представлена случайными величинами. Следовательно, характеристики состояния в модели определяются не однозначно, а через законы распределения их вероятностей. Моделируются, напр., стохастические процессы в теории массового обслуживания, в сетевом планировании и управлении и в других областях. При построении С. м. применяются методы корреляционного и регрессионного анализов, другие статистические методы. Другие названия С. м. — недетерминированная, вероятностная модель (см. также Вероятностная система).
Слайд 20
Автор: Орлова И.В., Половников В.А.
Издательство: Вузовский учебник
Год: 2008
В.В.
Васильев, Л.А. Симак, А.М. Рыбникова. Математическое и компьютерное моделирование
процессов и систем в среде MATLAB/SIMULINK. Учебное пособие для студентов и аспирантов. 2008 год. 91 стр.Компьютерное моделирование физических задач в Microsoft Visual Basic. Учебник Author: Алексеев Д.В.
СОЛОН-ПРЕСС, 2009 г





























