Общие методы решения квадратных уравнений.
Специальные методы решения квадратных уравнений.
Использование
свойства коэффициентов квадратного уравнения.Метод «переброски» старшего коэффициента.
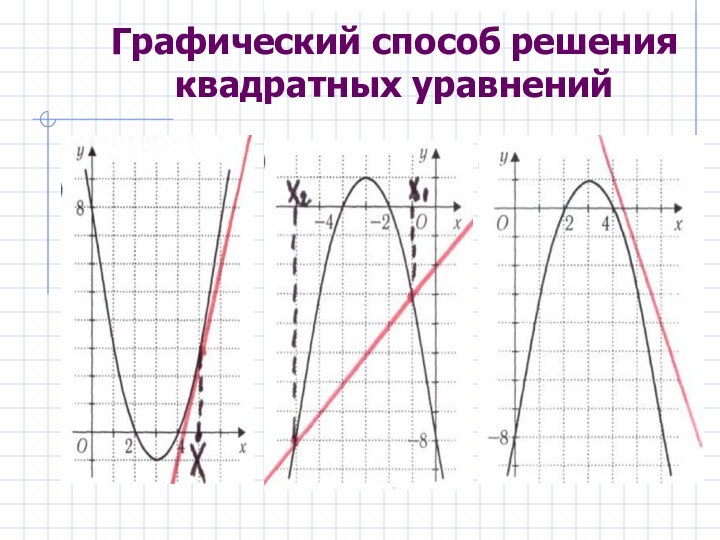
Графический способ решения квадратных уравнений.