Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему

Содержание

Развитие понятия числа
Тема: Числа и алгебраические выражения. Развитие понятия числа Основные числовые множества :- Ν – множество натуральных чисел.- Z – множество Алгебраические выражения Формулы сокращенного умножения нужно знать наизусть.Пусть а, b   R. Тогда:1. Квадрат суммы двух Формулы сокращенного умножения нужно знать наизусть.2. Квадрат разности двух выражений равен квадрату первого выражения Формулы сокращенного умножения нужно знать наизусть.3. Разность квадратов двух выражений равна произведению разности этих Формулы сокращенного умножения нужно знать наизусть.4. Куб суммы двух выражений равен кубу первого выражения Формулы сокращенного умножения нужно знать наизусть.5. Куб разности двух выражений равен кубу первого выражения Формулы сокращенного умножения нужно знать наизусть.6. Сумма кубов двух выражений равна произведению суммы первого Формулы сокращенного умножения нужно знать наизусть.7. Разность кубов двух выражений равна произведению разности первого Вычислить а) (40+1)2б) 982 Решение: а) Используя формулу квадрата суммы двух выражений, имеем(40+1)2 = =402 + 2 · Раскройте скобки: (x + 3у)2(4а -1)2(а + 3) (а2 - 3а + 9)(4x - 3y2) (4x + 3у2)(х - 2) (х2 + 2х + 4) Спасибо за внимание!!! Удачного дня!!!
Слайды презентации

Слайд 2 Развитие понятия числа

Развитие понятия числа

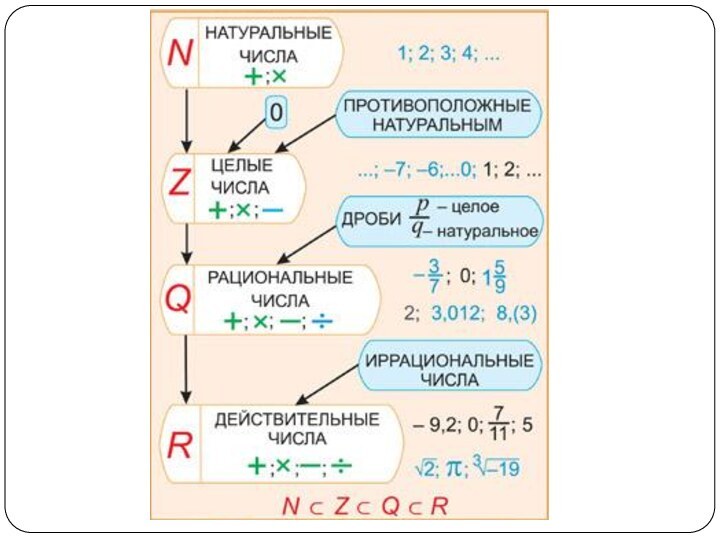
Слайд 3 Основные числовые множества :
- Ν – множество натуральных

Основные числовые множества :- Ν – множество натуральных чисел.- Z –

чисел.
- Z – множество целых чисел.
- Q – множество

рациональных чисел.
- R – множество действительных чисел.

Слайд 4

Слайд 5 Алгебраические выражения

Алгебраические выражения

Слайд 6 Формулы сокращенного умножения нужно знать наизусть.
Пусть а, b

Формулы сокращенного умножения нужно знать наизусть.Пусть а, b   R. Тогда:1. Квадрат суммы

  R. Тогда:
1. Квадрат суммы двух выражений равен квадрату первого выражения плюс

удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a + b)2 = a2 + 2ab + b2

Слайд 7 Формулы сокращенного умножения нужно знать наизусть.
2. Квадрат разности двух

Формулы сокращенного умножения нужно знать наизусть.2. Квадрат разности двух выражений равен квадрату первого

выражений равен квадрату первого выражения минус удвоенное произведение первого выражения

на второе плюс квадрат второго выражения.
(a - b)2 = a2 - 2ab + b2

Слайд 8 Формулы сокращенного умножения нужно знать наизусть.
3. Разность квадратов двух выражений

Формулы сокращенного умножения нужно знать наизусть.3. Разность квадратов двух выражений равна произведению разности

равна произведению разности этих выражений и их суммы.
a2 - b2 =

(a - b)(a + b)

Слайд 9 Формулы сокращенного умножения нужно знать наизусть.
4. Куб суммы двух выражений

Формулы сокращенного умножения нужно знать наизусть.4. Куб суммы двух выражений равен кубу первого

равен кубу первого выражения плюс утроенное произведение квадрата первого

выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(a + b)3 = a3 + 3a2b + 3ab2 + b3

Слайд 10 Формулы сокращенного умножения нужно знать наизусть.
5. Куб разности двух выражений

Формулы сокращенного умножения нужно знать наизусть.5. Куб разности двух выражений равен кубу первого

равен кубу первого выражения минус утроенное произведение квадрата первого

выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(a - b)3 = a3 - 3a2b + 3ab2 - b3

Слайд 11 Формулы сокращенного умножения нужно знать наизусть.
6. Сумма кубов двух выражений

Формулы сокращенного умножения нужно знать наизусть.6. Сумма кубов двух выражений равна произведению суммы

равна произведению суммы первого и второго выражения на неполный

квадрат разности этих выражений.
a3 + b3 = (a + b) (a2 - ab + b2)

Слайд 12 Формулы сокращенного умножения нужно знать наизусть.
7. Разность кубов двух выражений

Формулы сокращенного умножения нужно знать наизусть.7. Разность кубов двух выражений равна произведению разности

равна произведению разности первого и второго выражения на неполный

квадрат суммы этих выражений.
a3 - b3 = (a - b) (a2 + ab + b2)

Слайд 13

Слайд 14 Вычислить
а) (40+1)2
б) 982

Вычислить а) (40+1)2б) 982

Слайд 15 Решение:
а) Используя формулу квадрата суммы двух выражений, имеем
(40+1)2 =

Решение: а) Используя формулу квадрата суммы двух выражений, имеем(40+1)2 = =402 + 2


=402 + 2 · 40 · 1 + 12 =
=1600

+ 80 + 1 = 1681
б) Используя формулу квадрата разности двух выражений, получим
982 =
=(100 – 2)2 =
=1002 - 2 · 100 · 2 + 22 =
=10000 – 400 + 4 = 9604

Слайд 16 Раскройте скобки: 
(x + 3у)2
(4а -1)2
(а + 3) (а2 - 3а + 9)
(4x - 3y2) (4x + 3у2)
(х - 2)

Раскройте скобки: (x + 3у)2(4а -1)2(а + 3) (а2 - 3а + 9)(4x - 3y2) (4x + 3у2)(х - 2) (х2 + 2х + 4)

(х2 + 2х + 4)

  • Имя файла: .pptx
  • Количество просмотров: 129
  • Количество скачиваний: 0
- Предыдущая Екатерина II
Следующая - Великая тайна воды

Похожие презентации

Геометрические фигуры Геометрические фигуры 112
презентация космическое путешествие 1 класс презентация космическое путешествие 1 класс 103
Интерактивный тест по математике Сложение и вычитание натуральных чисел Интерактивный тест по математике Сложение и вычитание натуральных чисел 102
Презентация внеклассного мероприятия по математике Презентация внеклассного мероприятия по математике 104
Математика в спорте Математика в спорте 260
Презентация учебного проекта по математике Математические ребусы Презентация учебного проекта по математике Математические ребусы 346
Сто к одному Сто к одному 118
Арифметические действия с числами. Устный счет Арифметические действия с числами. Устный счет 90
Математическая разминка для 1 класса презентация к уроку по математике (1 класс) Математическая разминка для 1 класса презентация к уроку по математике (1 класс) 156
Тренажёр Помоги белочке! Тренажёр Помоги белочке! 232
Внетабличное умножение и деление. Внетабличное умножение и деление. 113
Римские цифры Римские цифры 135
Презентация по математике на тему Устный журнал. За страницами учебника математики? Презентация по математике на тему Устный журнал. За страницами учебника математики? 150
Конструкт непосредственно образовательной деятельности Счет и измерения в прошлом и сегодня план-конспект занятия по математике (старшая группа) по теме Конструкт непосредственно образовательной деятельности Счет и измерения в прошлом и сегодня план-конспект занятия по математике (старшая группа) по теме 188
Число и цифра 5 план-конспект урока по математике (1 класс) по теме Число и цифра 5 план-конспект урока по математике (1 класс) по теме 114
Построение сечений Построение сечений 104
Переменная - 03.02.2017 г. план-конспект урока по математике (3 класс) по теме Переменная - 03.02.2017 г. план-конспект урока по математике (3 класс) по теме 146
prilozhenie 1 prodolzhenie prilozhenie 1 prodolzhenie 88
Математическая головоломка Весёлые уравнения Математическая головоломка Весёлые уравнения 110
Презентация по математике Положение предметов на плоскости презентация к уроку по математике (1 класс) Презентация по математике Положение предметов на плоскости презентация к уроку по математике (1 класс) 139
Решаем, решаем, решаем!!! (по заданиям первой части ОГЭ 2014) Решаем, решаем, решаем!!! (по заданиям первой части ОГЭ 2014) 140
Функции нескольких переменных Функции нескольких переменных 142
Устный счет в пределах 10 презентация урока для интерактивной доски по математике (1 класс) Устный счет в пределах 10 презентация урока для интерактивной доски по математике (1 класс) 111
Системы счисления Системы счисления 93
Математика презентация урока для интерактивной доски по математике по теме Математика презентация урока для интерактивной доски по математике по теме 143
Конспект урока по математике 2 класс план-конспект урока по математике (2 класс) Конспект урока по математике 2 класс план-конспект урока по математике (2 класс) 121
ЗАДАЧИ ДЛЯ УСТНОГО СЧЕТА (2 КЛАСС) ЗАДАЧИ ДЛЯ УСТНОГО СЧЕТА (2 КЛАСС) 122
Аксиомы стереометрии и их простейшие следствия Аксиомы стереометрии и их простейшие следствия 91
Урок для 1 класса Решение задач разными способами. (УМК Начальная школа 21 века). презентация к уроку по математике (1 класс) Урок для 1 класса Решение задач разными способами. (УМК Начальная школа 21 века). презентация к уроку по математике (1 класс) 422
Презентация к уроку математики по теме: Представление о десятичных дробях Презентация к уроку математики по теме: Представление о десятичных дробях 132