- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теорема Фалеса
Содержание
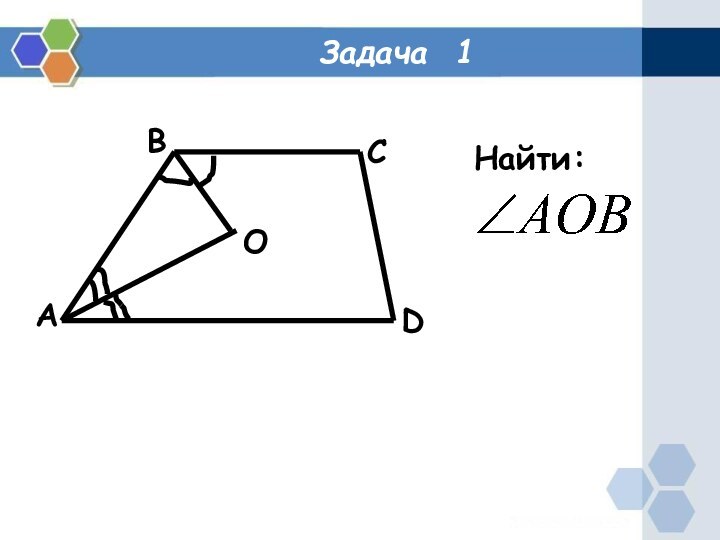
- 2. Задача 1ABDCOНайти:
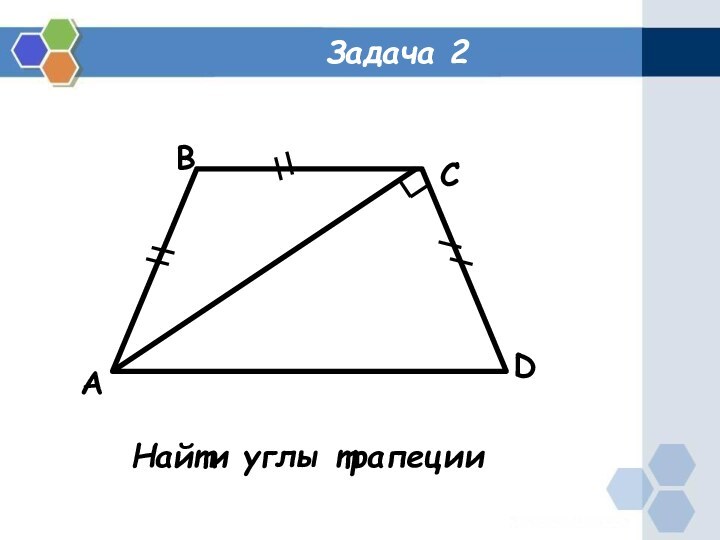
- 3. Задача 2ABCDНайти углы трапеции
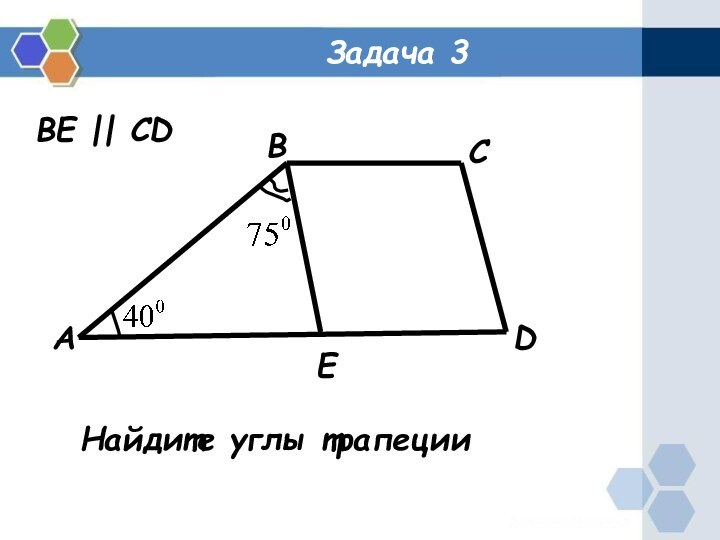
- 4. Задача 3АBCDEBE || CDНайдите углы трапеции
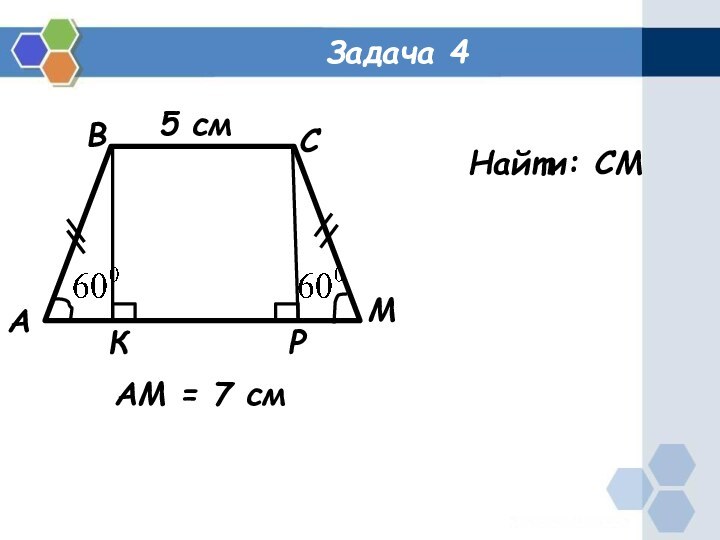
- 5. Задача 4АВСМРК5 смАМ = 7 смНайти: СМ
- 6. Теорема Фалеса Если на одной из двух прямых
- 7. Задача (деление отрезка на n равных частей)При
- 8. Средняя линия треугольникаСредней линией треугольника называется отрезок,
- 9. Признак средней линииЕсли отрезок параллелен стороне треугольника,
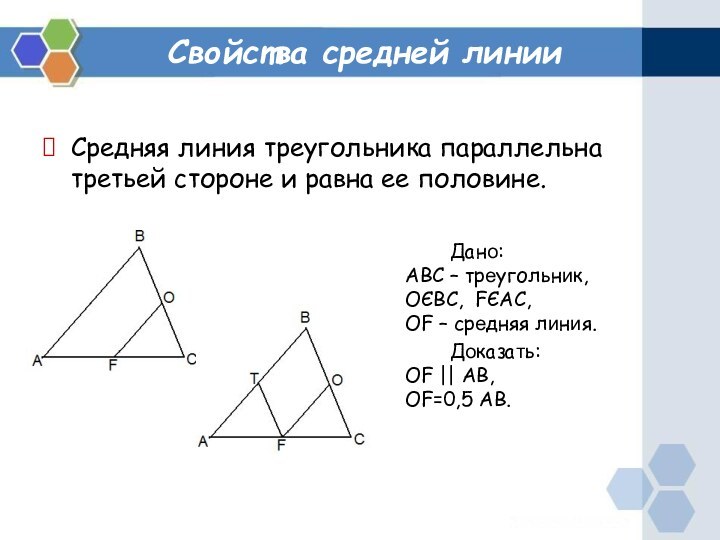
- 10. Свойства средней линии Дано: ABC – треугольник, ОЄBC,
- 11. Скачать презентацию
- 12. Похожие презентации
Задача 1ABDCOНайти:


Слайд 7
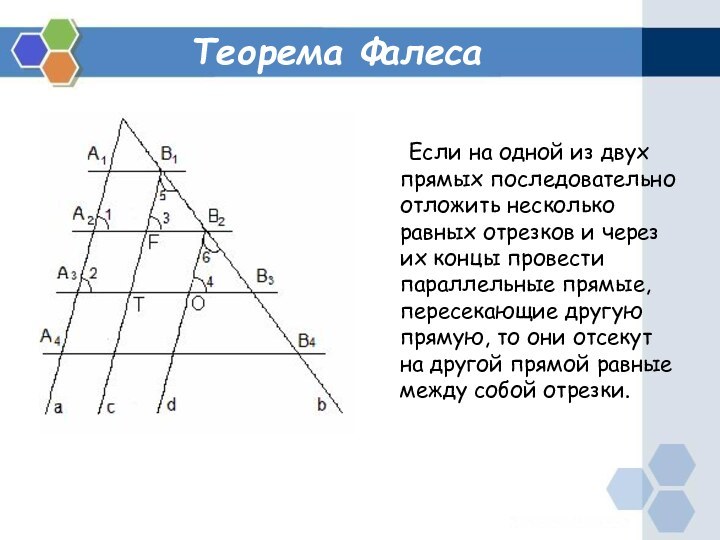
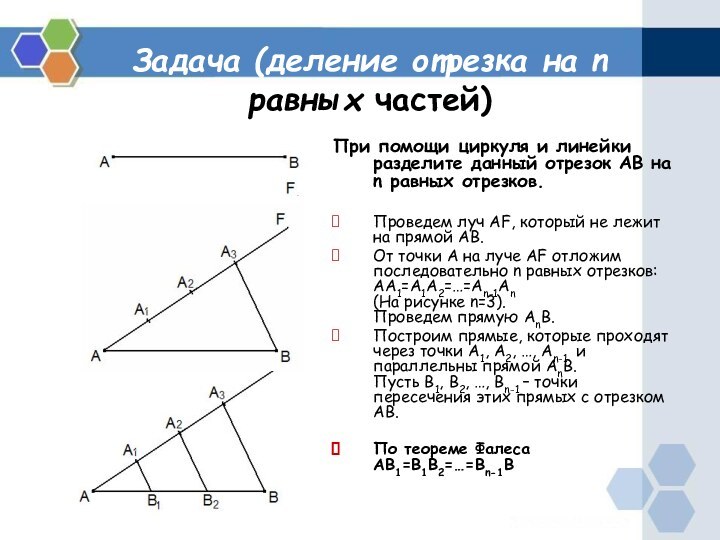
Задача (деление отрезка на n равных частей)
При помощи
циркуля и линейки разделите данный отрезок AB на n
равных отрезков.Проведем луч AF, который не лежит на прямой AB.
От точки A на луче AF отложим последовательно n равных отрезков: AA1=A1A2=…=An-1An (На рисунке n=3). Проведем прямую AnB.
Построим прямые, которые проходят через точки A1, A2, …, An-1 и параллельны прямой AnВ. Пусть B1, B2, …, Bn-1 – точки пересечения этих прямых с отрезком AB.
По теореме Фалеса AB1=B1B2=…=Bn-1B
Слайд 8
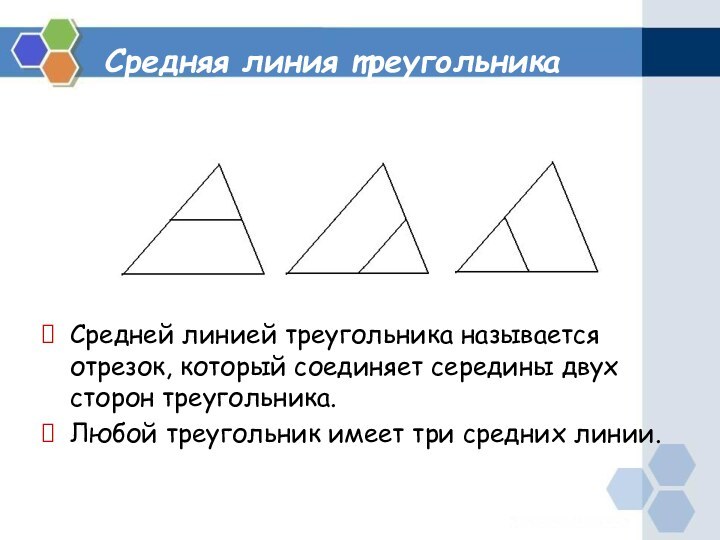
Средняя линия треугольника
Средней линией треугольника называется отрезок, который
соединяет середины двух сторон треугольника.
Любой треугольник имеет три средних
линии.
Слайд 9
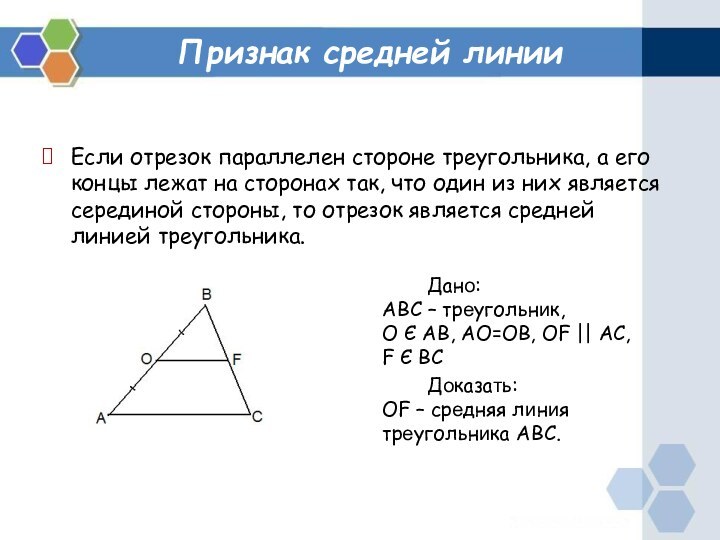
Признак средней линии
Если отрезок параллелен стороне треугольника, а
его концы лежат на сторонах так, что один из
них является серединой стороны, то отрезок является средней линией треугольника. Дано:
ABC – треугольник,
О Є AB, AO=OB, OF || AC,
F Є BC
Доказать:
OF – средняя линия треугольника ABC.