Слайд 2
Математика — самая абстрактная из наук, а музыка
— наиболее отвлеченное из искусств, это высшие выразители науки
и искусства.
Волошинов А.
Слайд 3
Цель работы: провести параллель между математикой и музыкой.
Задачи:
1) познакомиться с пифагорейским учением о связи между математикой
и музыкой;
2) разобрать основные правила консонанса и доказать их математическую природу;
3) в ходе исследования проверить, действуют ли пифагорейские правила консонанса до сих пор;
4) доказать благотворное влияние изучения музыки на математические способности и наоборот.
Методы исследования:
1) поиск, анализ и синтез различных источников информации: книг, статей, Интернет-ресурсов;
2) математический анализ музыкальных аккордов;
3) анкетирование.
Слайд 4
Актуальность темы состоит в том, что многие не
понимают, что математика и музыка родственны. Родители не принимают
во внимание тот факт, что музыкальное образование развивает способности к математике. Учитывая, что математика становится всё более популярным, но остаётся при этом не менее сложным предметом, ценность музыки и музыкального образования как вспомогательного должна повышаться.
Слайд 5
Музыка, математика – сколь родственны они.
Имре Мадач (венгерский
писатель)
Слайд 6
Пифагор — едва ли не самый популярный ученый
не только в античности, но и в наши дни.
Слайд 7
Заслуги пифагора
Пифагор учил математике, музыке, астрономии, медицине, принципам

политической деятельности, этике и многому другому. Из его школы
вышли выдающиеся политические и государственные деятели, историки, математики и астрономы.
Числа, равные сумме своих делителей, воспринимались как совершенные; дружественными называли пары чисел, из которых каждое равнялось сумме делителей другого. Пифагор впервые разделил числа на четные и нечетные, простые и составные, ввел понятие фигурного числа. В его школе были подробно рассмотрены тройки натуральных чисел, у которых квадрат одного равнялся сумме квадратов двух других.
Геометрия у Пифагора была подчинена арифметике. Это ярко проявилось в теореме, носящей его имя и ставшей в дальнейшем основой применения численных методов геометрии.
Пифагору приписывают систематическое введение доказательств в геометрию, создание планиметрии прямолинейных фигур, учение о подобии.
Пифагор одним из первых считал, что Земля имеет форму шара и является центром Вселенной.
Слайд 8
В математике, в познании количественных отношений, видели пифагорейцы
ключ к разгадке мировой гармонии, постижение которой и составляло
смысл их жизни.
Слайд 9
Отправным пунктом в пифагорейском учении о числе была
музыка. Именно в музыке была впервые обнаружена таинственная направляющая
роль чисел в природе. По преданию, сам Пифагор установил, что приятные слуху созвучия получаются лишь в том случае, когда длины струн, издающих эти звуки, относятся как целые числа первой четверки: 1:2, 2:3, 3:4. Это открытие потрясло Пифагора и долго вдохновляло его учеников на поиски новых числовых закономерностей в природе.
Слайд 10
С этого времени музыка, точнее теория музыки или
учение о гармонии, занимает почетное место в пифагорейской системе
знаний. «Музыкантов»-пифагорейцев интересовало не столько музыкальное искусство, сколько те математические пропорции и соотношения, которые, как считалось, лежат в основе музыки.
Идея музыкальных соотношений настолько увлекла пифагорейцев, что они пытались обнаружить их всюду.
Слайд 11
Музыка и астрономия были сведены пифагорейцами к анализу
числовых закономерностей, т. е. к арифметике и геометрии. Все
четыре дисциплины стали считаться математическими и называться одним словом — «математа».
Термины «наука» и «искусство» в далекие времена античности практически не различались. Пифагорейцы называли математику и музыку родными сестрами. Музыка пронизана математикой, как и математика полна поэзии и музыки. Это прекрасно чувствовали древние греки.
Слайд 12
Гаммой, или звукорядом, называется последовательность звуков некоторой музыкальной
системы, расположенных, начиная от основного звука, в восходящем или
нисходящем порядке.
Важнейшей характеристикой музыкального звука является его высота, представляющая отражение в сознании частоты колебания звучащего тела, например струны. Чем больше частота колебаний струны, тем «выше» представляется нам звук.
Слайд 13
Согласованное сочетание двух звуков называется консонансом, а несогласованное
— диссонансом.
Ладом называется приятная для слуха взаимосвязь музыкальных звуков,
определяемая зависимостью неустойчивых звуков от устойчивых, и прежде всего от основного устойчивого звука — тоники, и имеющая определенный характер звучания — наклонение.
Слайд 14
Высота тона (частота колебаний f) звучащей струны обратно
пропорциональна ее длине l.
Две звучащие струны дают консонанс лишь
тогда, когда их длины относятся как целые числа, составляющие треугольное число 10=1+2+3+4, т. е. как 1:2, 2:3, 3:4.
Если в качестве цены деления шкалы монохорда взять отрезок l, равный 1/12 длины струны монохорда l1, то вместе со всей струной монохорда длины l1 = 12l будут созвучны ее части длины l2 = 6l — звук на октаву выше (l2/l1 = 1/2), l3 = 9l — звук на квинту выше (l3/l1=2/3) и l4= 8l — звук на кварту выше (l4/l1=3/4). Это созвучие и определяющие его числа 6, 8, 9, 12 назывались тетрада (четверка).
Слайд 15
Квинта есть среднее гармоническое длин струн основного тона
l1 и октавы l2, а кварта — среднее арифметическое
l1 и l2.
Октава есть произведение квинты на кварту.
Октава так относится к квинте, как кварта к основному тону.
Октава делится на два неравных консонансных интервала — квинту и кварту. Интервал, дополняющий данный интервал до октавы, называется его обращением.
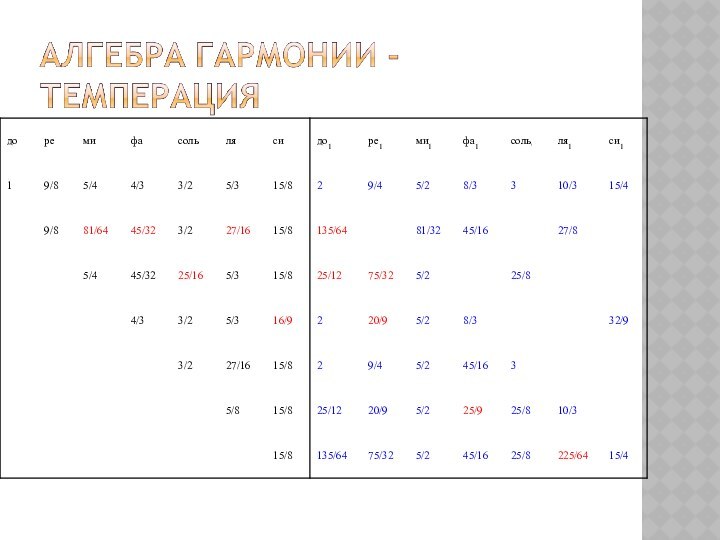
Слайд 16
К 1700 г. немецкий органист Андреас Веркмейстер осуществил
смелое и гениально простое решение: он отказался от совершенных
и несовершенных консонансов — квинт, кварт и терций, оставив в первозданной консонантной красе лишь одну октаву, и попросту разделил ее геометрически на 12 равных частей. Так в музыке восторжествовала темперация (лат. соразмерность), а новый двенадцатизвуковой строй был назван равномерно-темперированным.
Слайд 17
Вначале, разумеется, были попытки улучшить чистый строй, который
сохранял главный недостаток пифагорова строя: невозможность безболезненного перехода из
тональности в тональность. Естественным желанием при решении этой проблемы было увеличить количество звуков в октаве.
Слайд 19
Сейчас трудно сказать, кому первому пришла идея равномерно
разделить октаву на 12 равных частей. Идея эта была
подготовлена самой логикой развития музыкального строя и, как говорят в таких случаях, носилась в воздухе. Но изложение этой идеи мы находим в энциклопедическом труде Мерсенна «Универсальная гармония».
Слайд 20
Конечно, и в век Просвещения новое не всеми
воспринималось восторженно. Выдающийся немецкий композитор Георг Фридрих Гендель не
принял новшества. Отказ от совершенных консонансов возмущал его. К счастью, равномерная темперация нашла сторонника в лице сверстника Генделя, великого немецкого композитора и органиста Иоганна Себастьяна Баха.
Слайд 22
И все-таки является ли 12-звуковая равномерная темперация «абсолютной
истиной» в музыке? Разумеется, нет! Спор Баха и Генделя
продолжается. Музыкантов с особо тонким слухом раздражают «тупые» консонансы темперированного строя.
Поиски новых равномерных темперации продолжаются. Разработаны 24-, 48- и 53-звуковые равномерные темперации. На каждую из них специально написана музыка и сконструированы музыкальные инструменты. Но все они практического распространения не получили.
П.И.Чайковский
А.Н.Скрябин
С.Рихтер
Слайд 24
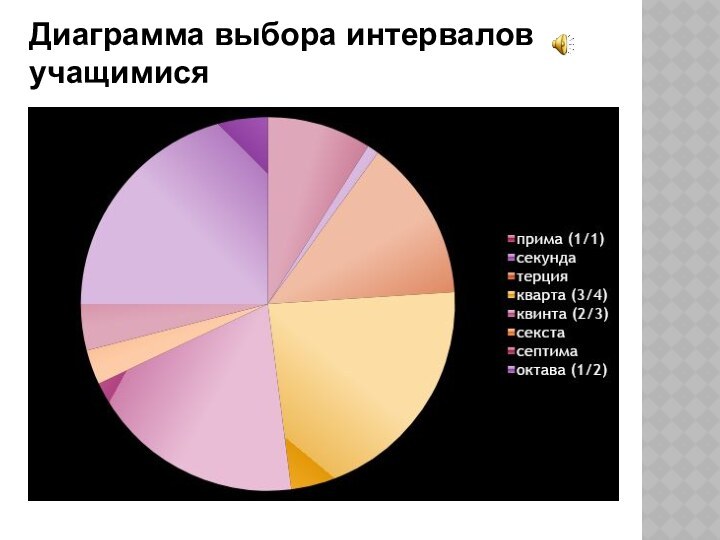
Диаграмма выбора интервалов учащимися
Слайд 25
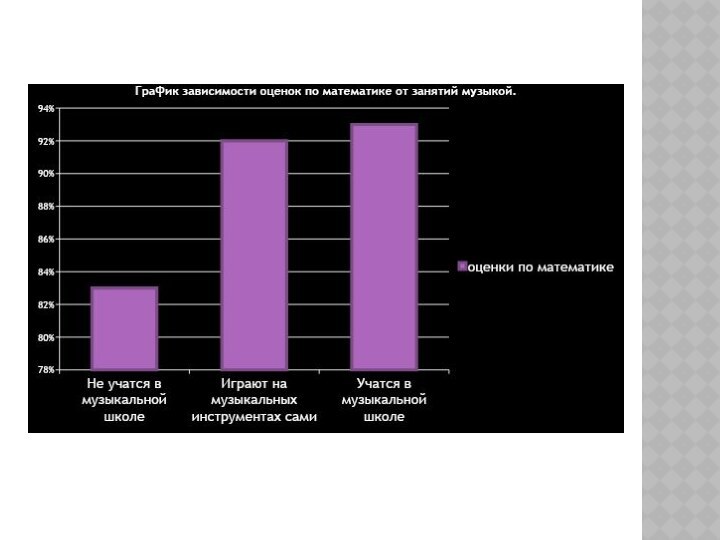
В ходе работы мы познакомились с пифагорейским учением
о математике и музыке; на основе его разработали правила
построения консонанса, доказали его математическую природу; с помощью исследования показали, что и сегодня пифагорейская теория консонансов может быть использована; убедились, что занятия музыкой благотворно влияют на математические способности учащихся. Таким образом, цель работы достигнута.
В нашем исследовании мы провели параллель между двумя, казалось бы несовместимыми науками: музыкой и математикой.