- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Объём пирамиды
Содержание
- 2. ВСПОМНИТЬ, ЧТО ТАКОЕ ПИРАМИДАНАУЧИТЬСЯ ПОЛЬЗОВАТЬСЯ ФОРМУЛОЙ НАХОЖДЕНИЯ ОБЪЁМА ПИРАМИДЫЦель работы:
- 3. ЧТО ТАКОЕ ПИРАМИДАТЕОРЕМАДОКАЗАТЕЛЬСТВОСЛЕДСТВИЕЗАМЕЧАНИЕЗАДАЧИ ДЛЯ РЕШЕНИЯВЫВОДПлан:
- 4. ПИРАМИДАПирамида – это многогранник, одной из граней
- 5. Объём пирамиды равен одной трети произведения площади основания на высотуТеорема
- 6. ДоказательствоРассмотрим треугольную пирамиду ОАВС с объёмом V,площадью
- 7. А1В1 параллельна АВ, поэтому треугольники ОА1В1 И
- 8. Применяя теперь основную формулу для вычисления объемов
- 9. Докажем теперь терему для произвольной пирамиды с
- 10. Объем V усеченной пирамиды, высота которой равна
- 11. В ходе доказательства теоремы об объеме пирамиды
- 12. №1 Найдите объем правильной треугольной пирамиды, высота
- 13. Мы вспомнили, что такое пирамида, научились пользоваться формулой нахождения объема пирамиды.Вывод
- 14. СПАСИБО ЗА ПРОСМОТР!!!
- 15. Скачать презентацию
- 16. Похожие презентации
ВСПОМНИТЬ, ЧТО ТАКОЕ ПИРАМИДАНАУЧИТЬСЯ ПОЛЬЗОВАТЬСЯ ФОРМУЛОЙ НАХОЖДЕНИЯ ОБЪЁМА ПИРАМИДЫЦель работы:














Слайд 4
ПИРАМИДА
Пирамида – это многогранник, одной из граней которой
служит многоугольник, а остальные грани – треугольники с общей
вершиной. В зависимости от числа боковых граней делятся на треугольные, четырехугольные и т.д. Перпендикуляр, опущенный из вершины на плоскость ее основания называется высотой.
Слайд 6
Доказательство
Рассмотрим треугольную пирамиду ОАВС с объёмом V,площадью основания
S и высотой h. Проведем ось Ох, где ОМ
– высота пирамиды и рассмотрим сечение А1 В1 С1 пирамиды плоскостью, перпендикулярной к оси Ох и, значит, параллельной плоскости основания. Обозначим через х абсциссу точки М1 пересечения этой плоскости с осью Ох, а через S(х) – площадь сечения. Выразим S(х) через S,h и х. треугольники А1 В1 С1 и АВС подобны.Слайд 7 А1В1 параллельна АВ, поэтому треугольники ОА1В1 И ОАВ
подобны. Следовательно, А1В1/АВ=ОА1/ОА. Прямоугольные треугольники ОА1М1 и ОАМ также
подобны ( они имеют общий острый угол с вершиной О). Поэтому ОА1/ОА=ОМ1/ОМ=x/h. Таким образом, А1В1/АВ=х/h. Аналогично доказывается, что В1С1/ВС=x/h и C1A1/CA=x/h. Итак, треугольники АВС и АВС подобны с коэффициентом подобия x/h. Следовательно, S (x)/S=x2/h, илиСлайд 9 Докажем теперь терему для произвольной пирамиды с высотой
h и площадью основания S. Такую пирамиду можно разбить
на треугольные пирамиды с общей высотой h. Выразим объем каждой треугольной пирамиды по доказанной нами формуле и сложим эти объемы. Вынося за скобки общий множитель 1/3h, получим в скобках сумму площадей оснований треугольных пирамид, т.е. площадь S основания исходной пирамиды. Таким образом, объем исходной пирамиды равен 1/3Sh. Теорема доказана.Слайд 10 Объем V усеченной пирамиды, высота которой равна h,
а площади оснований равны S и S1, вычисляется по
формулеСледствие
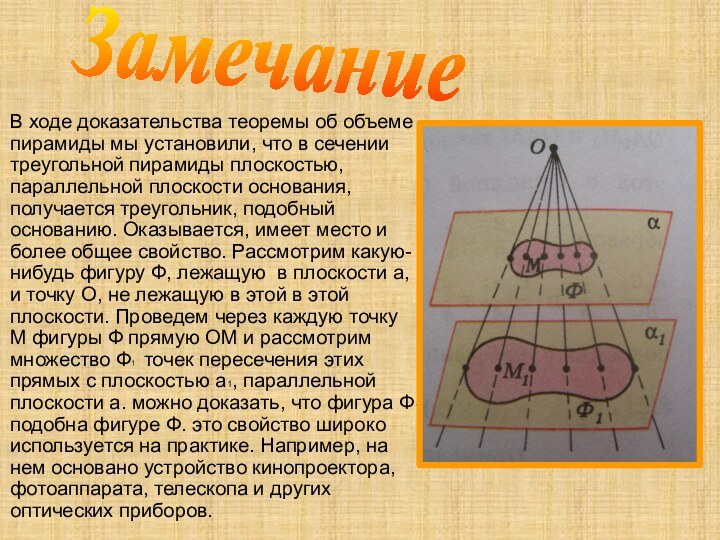
Слайд 11 В ходе доказательства теоремы об объеме пирамиды мы
установили, что в сечении треугольной пирамиды плоскостью, параллельной плоскости
основания, получается треугольник, подобный основанию. Оказывается, имеет место и более общее свойство. Рассмотрим какую-нибудь фигуру Ф, лежащую в плоскости а, и точку О, не лежащую в этой в этой плоскости. Проведем через каждую точку М фигуры Ф прямую ОМ и рассмотрим множество Ф1 точек пересечения этих прямых с плоскостью а1, параллельной плоскости а. можно доказать, что фигура Ф1 подобна фигуре Ф. это свойство широко используется на практике. Например, на нем основано устройство кинопроектора, фотоаппарата, телескопа и других оптических приборов.Замечание
Слайд 12 №1 Найдите объем правильной треугольной пирамиды, высота которой
равна 12 см, а сторона основания равна 13 см.
№2
В правильной треугольной пирамиде плоский угол при вершине равен а, а сторона основания х. найдите объем пирамиды.№3 Найдите объем пирамиды с высотой h, если h=2 м, а основанием служит квадрат со стороной 3 м.
ЗАДАЧИ ДЛЯ РЕШЕНИЯ