Слайд 2
План:
1. История развития теории и методики математики
в XVII-XIX в.в.
2. История развития теории и методики
математики в начале XX века.
3. История развития теории и методики математики в середине XX века.
4. Проблема математического развития дошкольников на современном этапе.
Слайд 3
1. История развития теории и методики математики в
XVII-XVIII вв.
В XVII-XIХ вв. Я.А. Коменский, Дж. Локк,
И. Г. Песталоцци, К. Д. Ушинский, Л. Н. Толстой, М. Монтессори и др. пришли к выводу о необходимости специальной математической подготовки детей дошкольного возраста.
Формирование у них математических знаний (о размере, измерении, времени и пространстве) рассматривалось с точки зрения практической целесообразности.
Этот период становления методики называют эмпирическим, так как основные идеи математического развития обобщали личный опыт педагогов.
Слайд 4
Большой вклад в методику математики внес
Иоганн Генрих
Песталоцци (1746-1827)
Он назвал свою теорию образования «элементарной», так как
считал, что развитие ребенка должно начинаться с наипростейших элементов и двигаться к сложным.
Слайд 5
И. Г. Песталоцци придавал решающее значение наглядности в
обучении как средству развития у ребенка умения в процессе
наблюдения сравнивать предметы, выявляя их общие и отличительные признаки и соотношения между ними.
Им была разработана система расположенных в определенной последовательности упражнений с целью привести в движение присущее природным силам человека стремление к деятельности.
Слайд 6
Он первый стал обучать детей геометрии и предлагал
последовательный переход от изучения формы к измерениям, рисованию и
письму.
Первоначальное обучение счету И. Г. Песталоцци предложил начинать с единицы: на основе сочетания и разъединения единиц давать детям наглядные представления о свойствах чисел.
Слайд 7
Большой интерес представляет методика
Марии Монтессори (1870-1952),
которая
связывает формирование математических представлений и сенсорное развитие детей.
Слайд 8
Наглядный дидактический материал, разработанный
М. Монтессори, позволяет активизировать работу зрительных, слуховых, тактильных анализаторов.
Упражнения со специально разработанными пособиями имеют цель, развить представления детей о количестве, форме, величине, пространстве и времени.
Слайд 10
Когда еще не существовало таких терминов как «гуманизация»
и «личностно-ориентированный подход», М. Монтессори обращалась к
педагогам и родителям с призывом относиться к ребенку как к личности, не унижать его человеческое достоинство, не рассматривать как орудие проявления своей воли, а самое главное - доверять в стремлении к самообразованию.
Слайд 11
Занимаясь с детьми, имеющими нарушения развития, она добилась
действительно высоких результатов обучения.
Важно было то, что при
этом использовались не медикаментозные, а педагогические средства воздействия.
Введение созданных ею методов в практику массовых школ привело к еще более внушительным результатам.
Слайд 12
Взгляды М. Монтессори повлияли на организацию математического образования
дошкольников в России.
Ее последователями стали Е. И. Тихеева,
Ю. И. Фаусек, которые воплотили идеи М. Монтессори в педагогическую практику и адаптировали их к отечественным условиям.
Слайд 13
2. История развития теории и методики математики в
начале ХХ в.
В начале XX в. появилась необходимость
детального изучения механизмов, позволяющих преподавать математику дошкольникам.
На этом этапе началось становление теории и методики математического развития дошкольников, определились содержание, методы и приемы работы с детьми.
Свой вклад в изучения данной проблемы внесли как зарубежные (Ж. Пиаже и др.), так и отечественные исследователи (Ф. Н. Блехер, Л. В. Глаголева, Е. И. Тихеева, Л. К. Шлегер).
Слайд 15
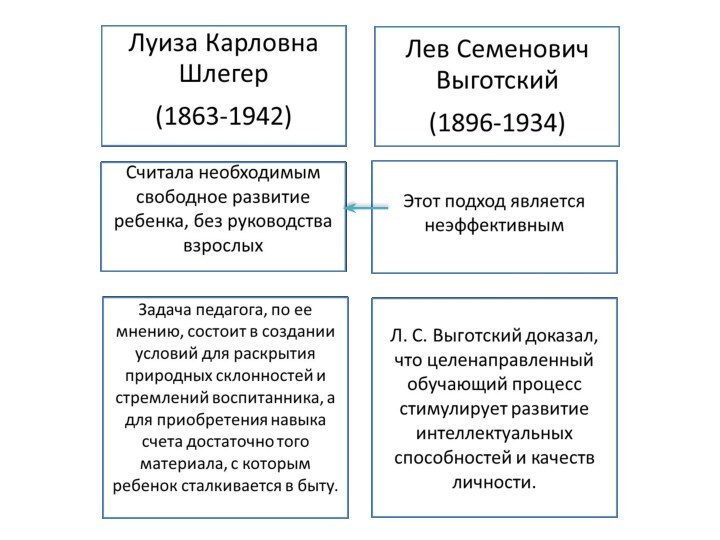
Л. С. Выготский видел один из источников развивающей
роли обучения в содержании получаемых знаний, в усвоении детьми
научных понятий.
Поэтому при обучении каждому учебному предмету важно максимально учитывать резервы, скрытые как в содержании учебного так и в методике обучения, и направлять их на развитие мыслительных процессов и эмоционально-волевой сферы.
В свою очередь обеспечение максимально возможного общего развития будет способствовать росту эффективности обучения.
Слайд 16
Взгляды Л. С. Выготского определили дальнейшее развитие
методики формирования математических представлений.
Л. К. Шлегер значительно увеличила объем
изучаемого материала и уделила значительное внимание счету, решению арифметических задач, долям, сравнению предметов по величине и измерению, геометрическим фигурам.
Основным средством обучения Л. К. Шлегер считала создание развивающей среды с помощью дидактических материалов М. Монтессори.
Слайд 17
О целенаправленном изучении процессов математического развития дошкольников впервые
было сказано Блехер
Фани Наумовной
(1892-1977)
Основной путь математического
развития детей по методике, разработанной Ф. Н. Блехер, - использование дидактических игр, игровых занимательных упражнений.
Слайд 18
После того, как на III (1924) и на
IV (1928) съездах по дошкольному воспитанию вопрос о программе
для детского сада и принципах ее построения был выделен в специальный раздел, а в 1929 г. вышло методическое письмо Наркомпроса «О связи дошкольных учреждений со школой и о планировании работы», Ф. Н. Блехер подключилась к разработке «Программы и внутреннего распорядка детского сада», где определила подходы к обучению дошкольников математике, сказала о необходимости развития представлений о счете, величине, форме, пространстве и времени.
Слайд 19
Несмотря на прогрессивную идею научного подхода к формированию
математических представлений у дошкольников, Ф. Н. Блехер недооценивала роль
фронтальных занятий, считала, что надо содействовать саморазвитию ребенка, а не вмешиваться в его развитие.
Тем не менее ее труды сыграли положительную роль в дальнейшем развитии методики.
Слайд 20
Елизавета Ивановна Тихеева (1867 — 1943)
так же,
как и Л. К. Шлегер, отрицала значение систематического обучения,
однако интересовалась его содержанием и предложила определенную последовательность ознакомления дошкольников с математикой.
Слайд 21
3. История развития теории и методики математики в
середине ХХ в.
В середине XX в. на становление
теории и методики формирования математических представлений у детей стали оказывать влияние фундаментальные исследования в области психологии и педагогики.
Начался процесс изучения психологии математического развития (П. Я. Гальперин, В. В. Давыдов, Г. С. Костюк, Н. А. Менчинская, Н. И. Непомнящая и др.).
Слайд 22
Основным вопросом, который требовал решения, было определение подходов
к формированию представлений о числе и счете.
Изучение чисел
в процессе овладения предметными действиями стало основой в концепции П. Я. Гальперина, Л. С. Георгиева, В. В. Давыдова, Г. А. Корнеева и др.
Одну из главных задач изучения этой темы авторы видят в том, чтобы приучить детей систематически пользоваться меркой и результатами измерения.
Такой подход позволяет показать относительность количественных отношений между величинами.
Слайд 23
Леушина Анна Михайловна
(1898-1982)
научно обосновала дидактическую систему
формирования элементарных математических представлений
Слайд 24
А. М. Леушина считает, что только целенаправленная деятельность
детей на занятии позволяет достичь высоких результатов обучения.
Опираясь
на теорию деятельности А. Н. Леонтьева, методика формирования математических представлений предполагает:
создание положительной мотивации обучения математике,
постановку конкретных целей и
разработку заданий, позволяющих их достичь.
Слайд 25
А. М. Леушина сформулировала требования к занятиям,
разработала
пути использования дидактических принципов, методов и средств обучения, благодаря
которым не только усваиваются необходимые знания, формируются умения и навыки, но и развиваются познавательные способности.
А.М. Леушина и преподаватели кафедры дошкольной педагогики Ленинградского государственного педагогического института им. А. И. Герцена (в 1944-1973 гг. заведующая кафедрой дошкольной педагогики).
Слайд 26
4. Проблема математического развития детей старшего дошкольного и
младшего школьного возраста с речевыми нарушениями на современном этапе
На современном этапе проблема математического развития дошкольников актуализировалась рядом причин:
повысились возрастные возможности детей в усвоении математического содержания,
возросли требования школы к математической подготовке дошкольников,
изменились социальные условия и отношение взрослых к воспитанию и образованию детей.
Слайд 27
Благодаря идеям гуманизации педагогического процесса учителям и воспитателям
предоставляются широкие возможности в выборе программ математического развития, в
использовании разнообразных моделей и технологий обучения дошкольников.
Слайд 28
В исследованиях Л. А. Венгера, А. А. Смоленцевой,
А. А. Столяра, Л. И. Тихоновой и др. показана
целесообразность использования различных игр в обучении детей математике и развитии интереса к обучению.
В дошкольном возрасте учебная деятельность начинает развиваться в процессе игры (Л. А. Венгер, В. В. Давыдов), поэтому ребенок должен обучаться, играя.
Слайд 29
В игре моделируются логические и математические конструкции, решаются
задачи, которые способствуют ускорению формирования и развития логических структур
мышления.
В процессе игры создаются благоприятные условия для применения математических знаний, их активного и самостоятельного использования на практике, развивается интерес к математическому содержанию
Слайд 30
Использование игровых методов на занятиях по формированию элементарных
математических представлений способствует тому, что у детей появляется интерес
к учению, развиваются творческое начало, инициатива, настойчивость, самоконтроль, которые, в дополнение к интеллекту и приобретенным умениям и навыкам, составляют творческую направленность личности
Слайд 31
Задачами математической подготовки являются не только формирование знаний
о множестве, числе, величине, форме, пространстве и времени навыков
и умений в счете, вычислениях, измерении, моделировании, общеучебных умений, но и
развитие познавательных интересов и способностей, словесно-логического мышления, общее интеллектуальное развитие ребенка.
Добиться успешного усвоения учебного материала позволяет использование различных методов, приемов и средств обучения.
Выбор методов обучения зависит от поставленных целей и задач, возраста детей, содержания изучаемого материала и этапа занятия.
Слайд 32
Несмотря на теоретическую обоснованность дидактических условий обучения математике
в дошкольных учреждениях В. А. Козлова, А. М. Леушина,
3. А. Михайлова, Н. И. Непомнящая, Е. И. Щербакова и др. говорят о трудностях формирования математических представлений у детей.
Основные ошибки при выполнении математических заданий допускаются из-за неумения осуществлять самоконтроль, пояснять свои действия, включать математические термины в речевое высказывание.
Выделенные особенности проявляются в большей степени у дошкольников, имеющих речевую патологию.
Это связано с особенностями развития и структурой дефекта.