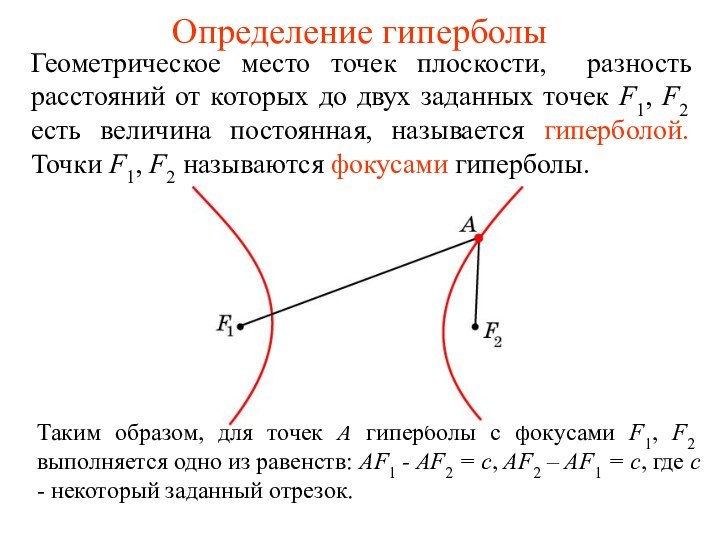
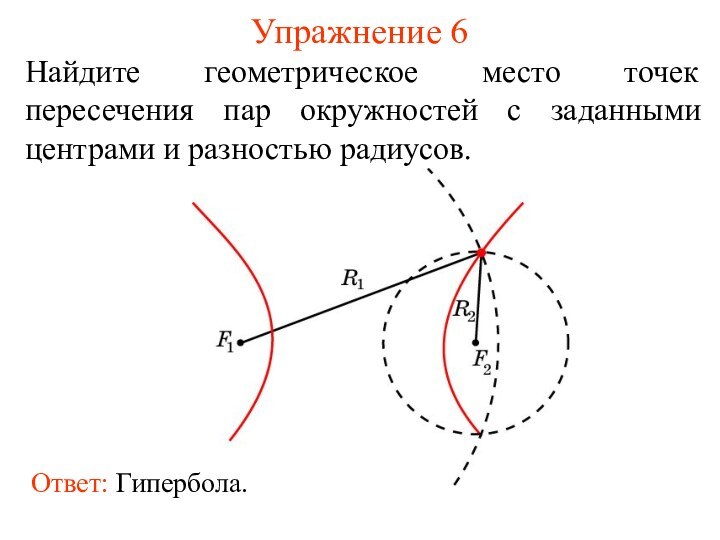
которых до двух заданных точек F1, F2 есть величина
постоянная, называется гиперболой. Точки F1, F2 называются фокусами гиперболы.Таким образом, для точек А гиперболы с фокусами F1, F2 выполняется одно из равенств: AF1 - AF2 = c, AF2 – AF1 = c, где c - некоторый заданный отрезок.