Факторы, влияющие на значимость оценок
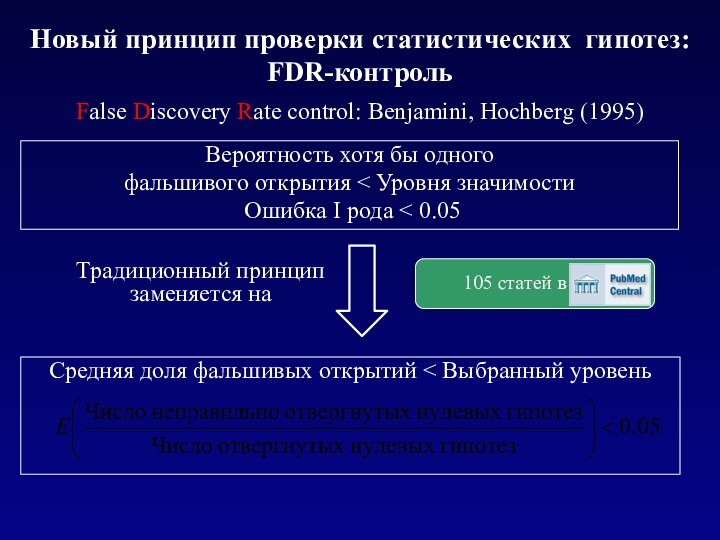
Объединение выборок и метаисследования Учет множественности сравнений
Темы для обсуждения
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть




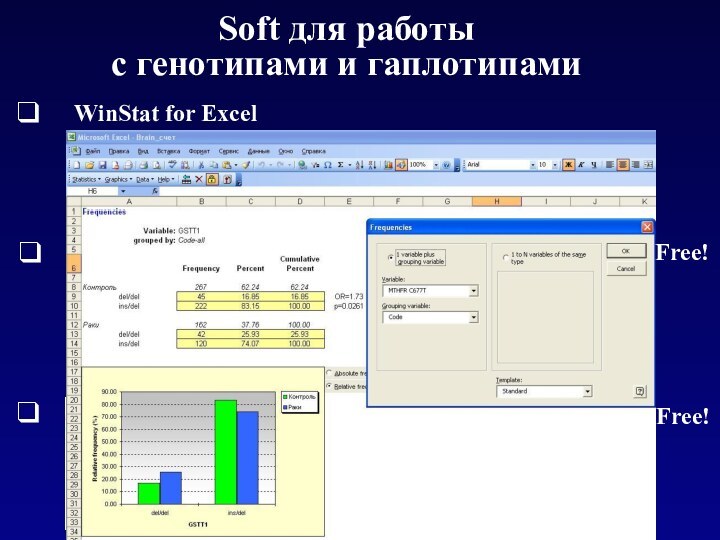








Учет множественности сравнений
Темы для обсуждения
Фенотип - количественный признак
(например: вес, содержание кальция, частота аберраций)
Кроме этого в обоих случаях можно
строить различные регрессионные модели:
Зависимая переменная – признак (фенотип),
независимыми переменные – генотипы.
Например так: A/A - 0, A/T - 1, T/T - 2
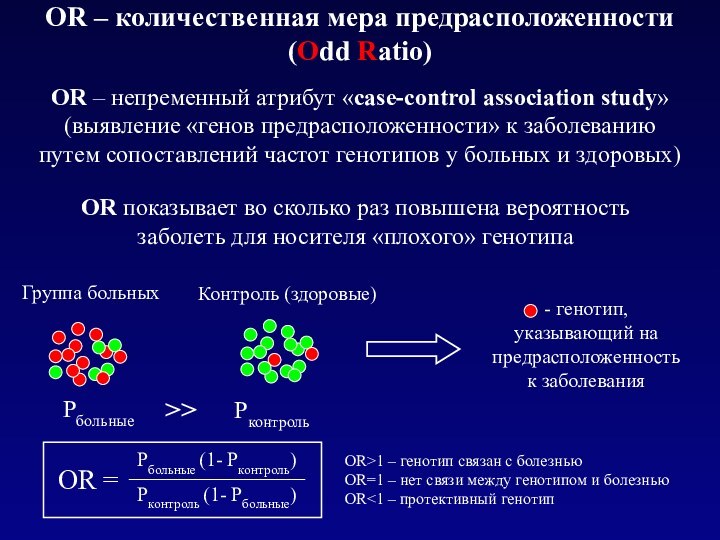
OR – количественная мера предрасположенности
(Odd Ratio)
OR>1 – генотип связан с болезнью
OR=1 – нет связи между генотипом и болезнью
OR<1 – протективный генотип
OR показывает во сколько раз повышена вероятность заболеть для носителя «плохого» генотипа
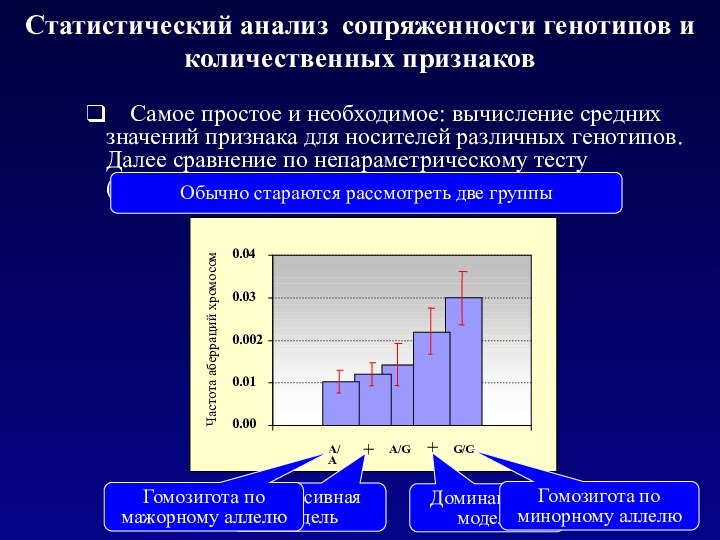
Гомозигота по мажорному аллелю
Гомозигота по минорному аллелю
Обычно стараются рассмотреть две группы
Группа людей с нулевым уровнем аберраций
Статистический анализ сопряженности генотипов и количественных признаков
Далее вычисляется OR
и значимость по точному критерию Фишера.
В данном примере риск возникновения аберраций у носителей минорного аллеля G равен OR=2,1 и р=0,015
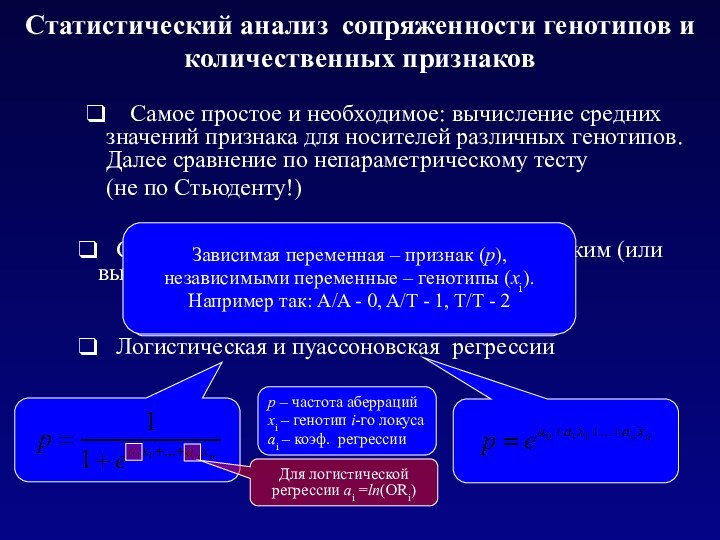
р – частота аберраций
xi – генотип i-го локуса
аi – коэф. регрессии
Нелинейные многомерные регрессии,
реализованные в пакетах Statistica и SPSS
Самое простое и необходимое: вычисление средних значений признака для носителей различных генотипов. Далее сравнение по непараметрическому тесту
(не по Стьюденту!)
Статистический анализ сопряженности генотипов и количественных признаков
Зависимая переменная – признак (р),
независимыми переменные – генотипы (xi).
Например так: A/A - 0, A/T - 1, T/T - 2
Учет множественности сравнений
Темы для обсуждения
Ошибка II рода ()
Вероятность принять неправильную нулевую гипотезу = Вероятность не обнаружить существующие различия = Вероятность упустить открытие
Мощность теста = 1- Ошибка II рода =
Вероятность правильно отвергнуть нулевую гипотезу
Вероятность не упустить открытие
Нулевая гипотеза – обычно предположение об отсутствии различий = 2 выборки из одной генеральной совокупности
Традиционно биолог ориентирован на контроль
ошибки I рода (через уровень значимости),
т.е. на гарантии отсутствия ложных открытий,
… и при этом мало заботится о возможности
упустить открытие (ошибка II рода)
С увеличением объема выборки мощность теста
(вероятность не упустить открытие)
всегда возрастает
Крайний случай:
«критерий» св. Фомы Неверующего (0033)
Ошибка I рода = 0 Ошибка II рода = 1
Ошибка I рода (вероятность фальшивого открытия)
слабо зависит от объемов выборок,
если они сравнимы по величине
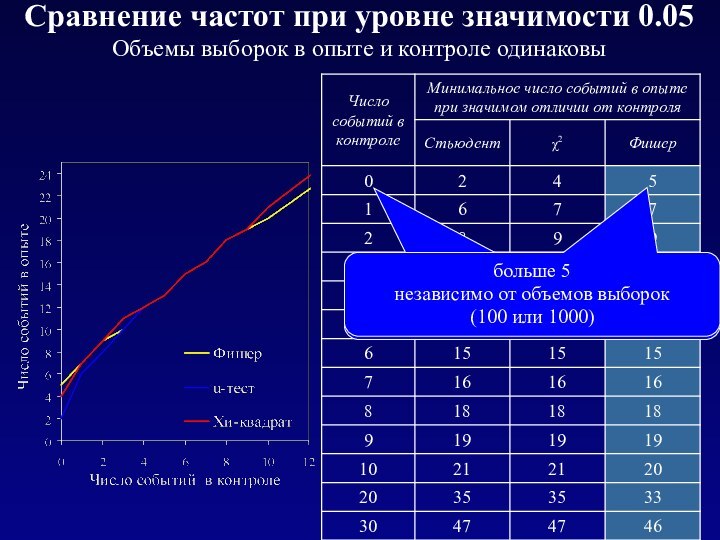
больше 5
независимо от объемов выборок
(100 или 1000)
Учет множественности сравнений
Темы для обсуждения
Индекс рассеяния для биномиальных выборок
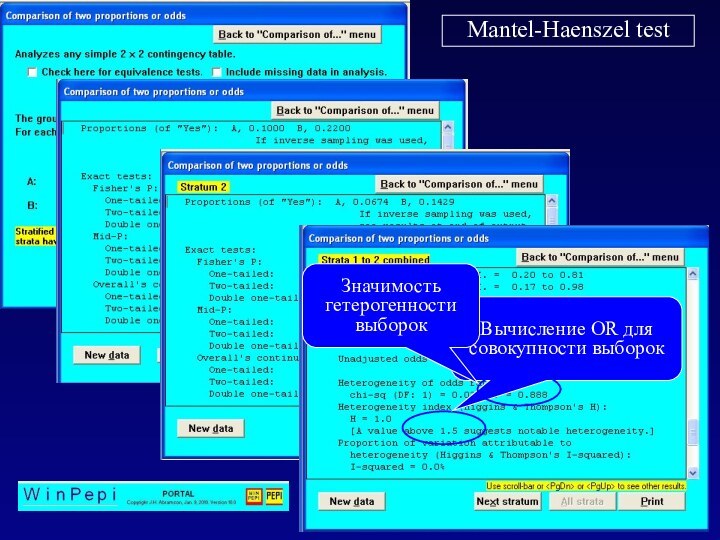
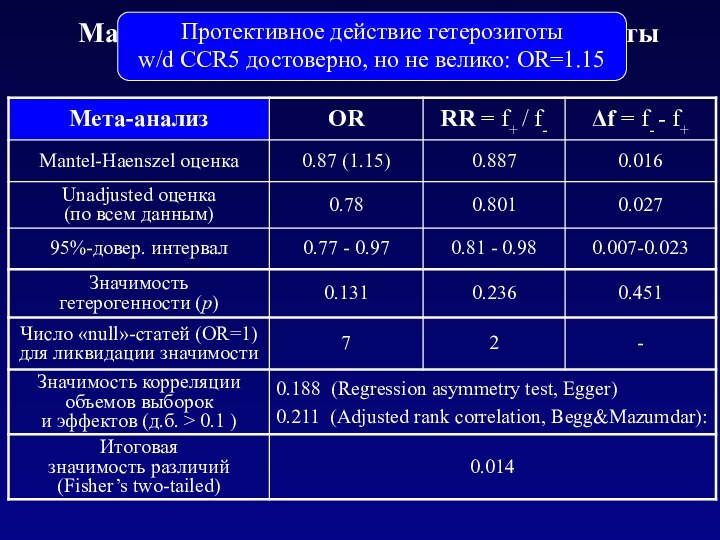
Mantel-Haenszel test
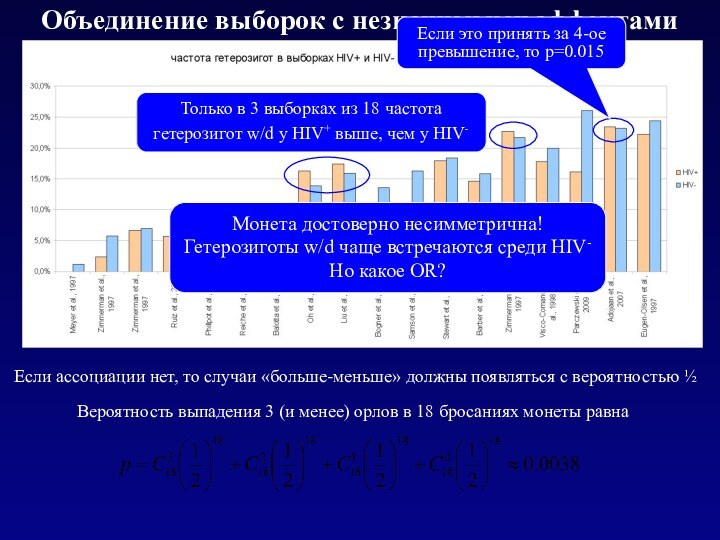
Монета достоверно несимметрична!
Гетерозиготы w/d чаще встречаются среди HIV-
Но какое OR?
Учет множественности сравнений
Темы для обсуждения
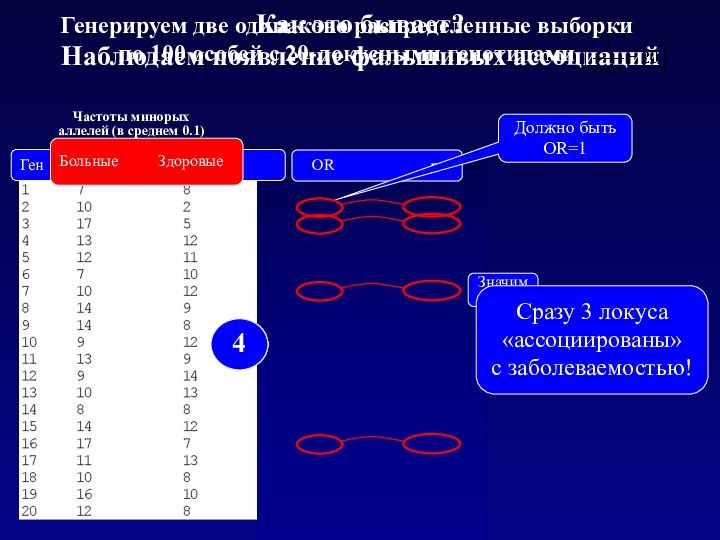
Ген Выборка 1 Выборка 2
Больные Здоровые
1
Должно быть
OR=1
2
3
4
Сразу 3 локуса
«ассоциированы»
с заболеваемостью!
Частоты минорых аллелей (в среднем 0.1)
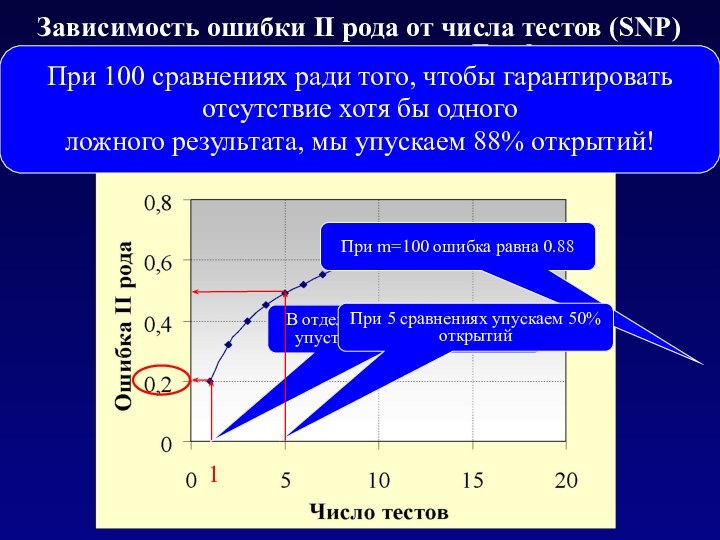
При 100 сравнениях ради того, чтобы гарантировать
отсутствие хотя бы одного
ложного результата, мы упускаем 88% открытий!
При m=100 ошибка равна 0.88
В отдельном тесте вероятность упустить открытие равна 0.2
При 5 сравнениях упускаем 50% открытий
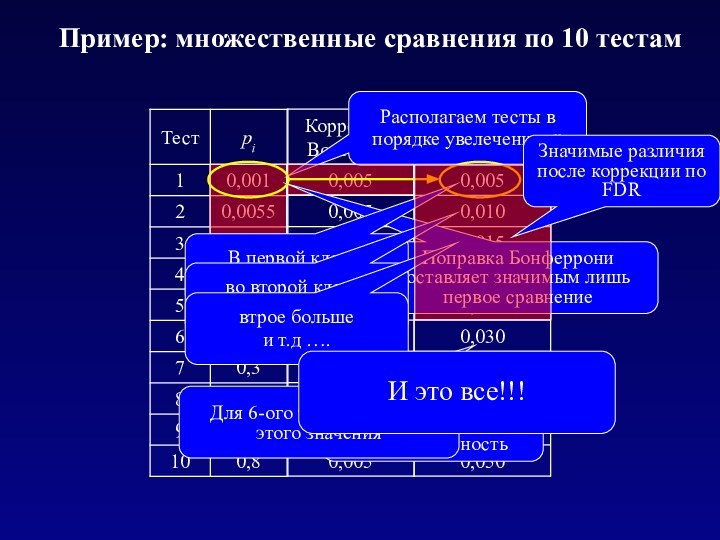
В первой клетке
как у Бонферрони,
во второй клетке
вдвое больше,
втрое больше
и т.д ….
Для 6-ого теста p больше этого значения
Значимые различия после коррекции по FDR
И это все!!!
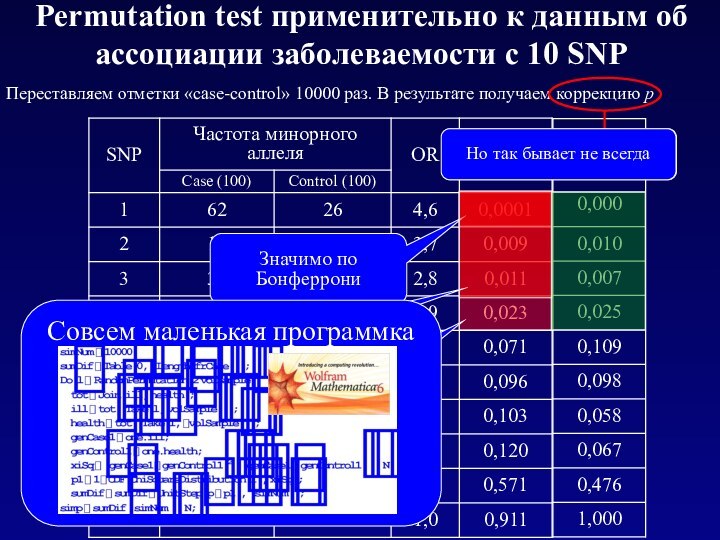
Тем самым мы отказываемся от попыток
вычислить значимость различий.
Вместо этого мы ее «измеряем» экспериментально,
разыгрывая ситуацию на компьютере
Точный тест Фишера – это тоже permutation test,
только реализованный аналитически (р вычисляется
по формулам комбинаторной теории вероятностей)