- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Основы тригонометрии
Содержание
- 2. 4567891011121314Тригонометрическая рулетка151617финиш23331318
- 3. Определение синуса, косинуса и тангенса угла.хуsinα=ycosα=xtgα=у/хМ(х;у)α
- 4. АСВСоотношения между углами и сторонами прямоугольного треугольникаЭти
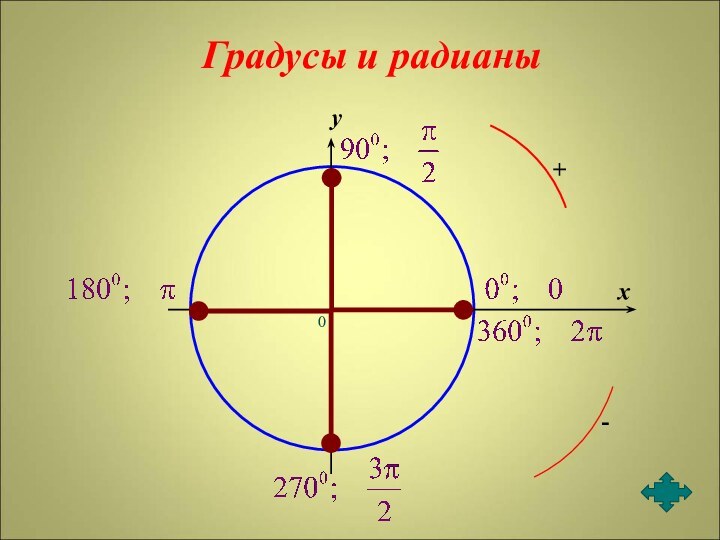
- 5. 0xyГрадусы и радианы
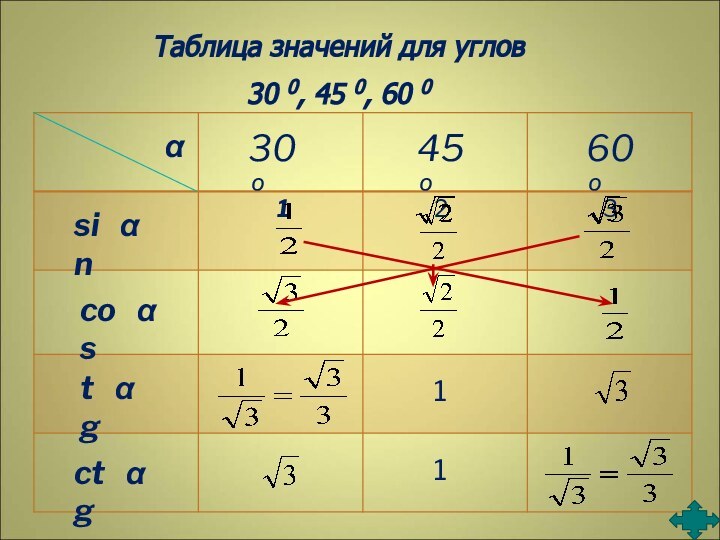
- 6. 30º60º45ºαsinααααcostgctg12311Таблица значений для углов 30 0, 45 0, 60 0
- 7. Знаки тригонометрических функций.IIIIIIIVsin α > 0 cos
- 8. Тригонометрические тождества
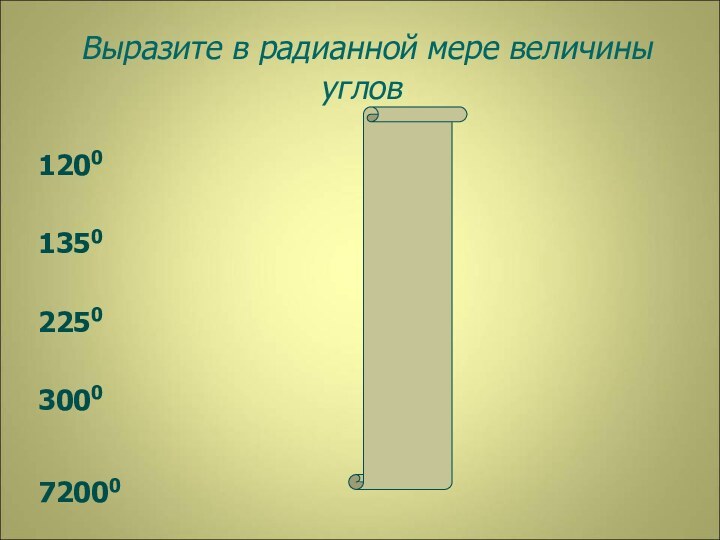
- 9. Выразите в радианной мере величины
- 10. Выразите в градусной мере величины углов -
- 11. Найдите координаты точек единичной окружностиР900
- 12. Сравните углы α и β выраженные в
- 13. Определите знак значения выражения sin1000 cos1000
- 14. Определите четверть, в которой расположена точка, полученная
- 15. Найдите значение выражения3tg00+2cos900+3sin2700-3cos1800
- 16. Может ли косинус или синус быть равным:0,75
- 17. Решите уравнения cos0,5x=0
- 18. Решите задачу.В треугольнике ABC угол C равен 900, АВ=143, АС=55. Найдите tgA. АВС
- 19. Решите задачу.В равнобедренном треугольнике ABC с
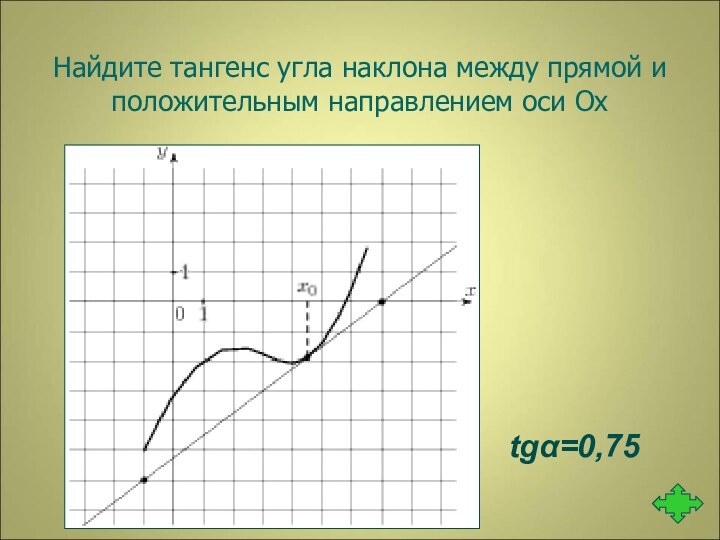
- 20. Найдите тангенс угла наклона между прямой и положительным направлением оси Охtgα=0,75
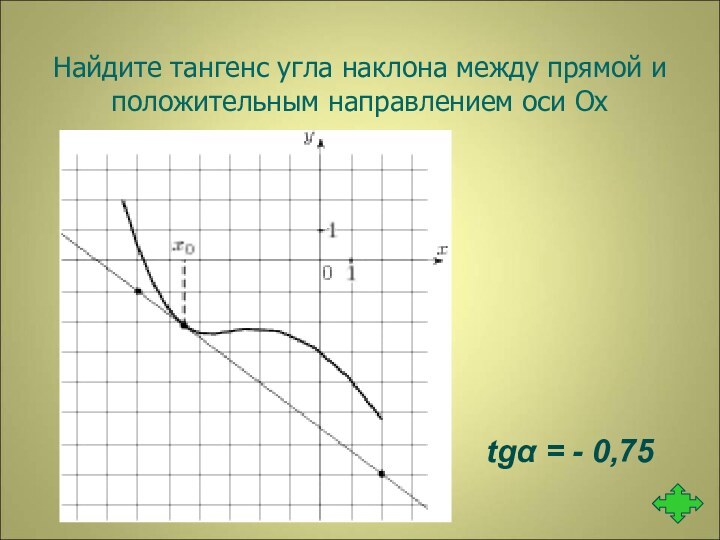
- 21. Найдите тангенс угла наклона между прямой и положительным направлением оси Охtgα = - 0,75
- 22. 1 .Найдитеесли2.Найдите tgα, если3.Найдите 3 cosα, еслииНайдите значение выражения
- 23. Нахождение углов в задачах прикладного содержания
- 24. Нахождение углов в задачах прикладного содержанияМячик броcают
- 25. Нахождение углов в задачах прикладного содержанияКатер должен
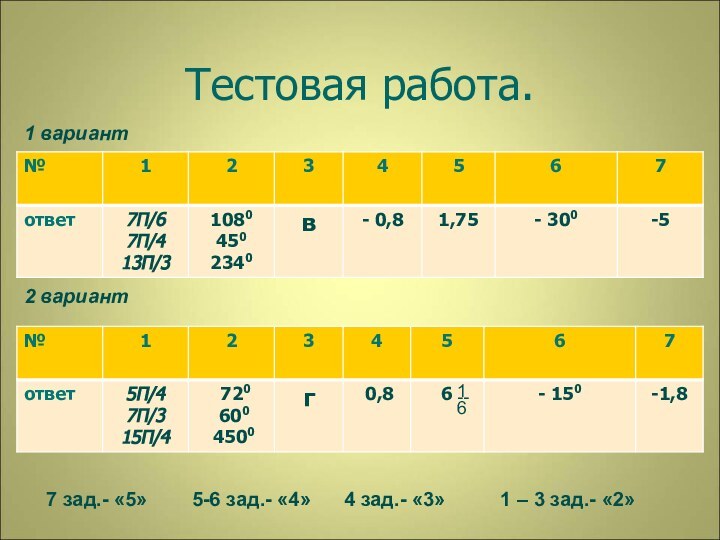
- 26. Тестовая работа.
- 27. Тестовая работа.1 вариант2 вариант1--67 зад.- «5»
- 28. Скачать презентацию
- 29. Похожие презентации
4567891011121314Тригонометрическая рулетка151617финиш23331318
Слайд 4
А
С
В
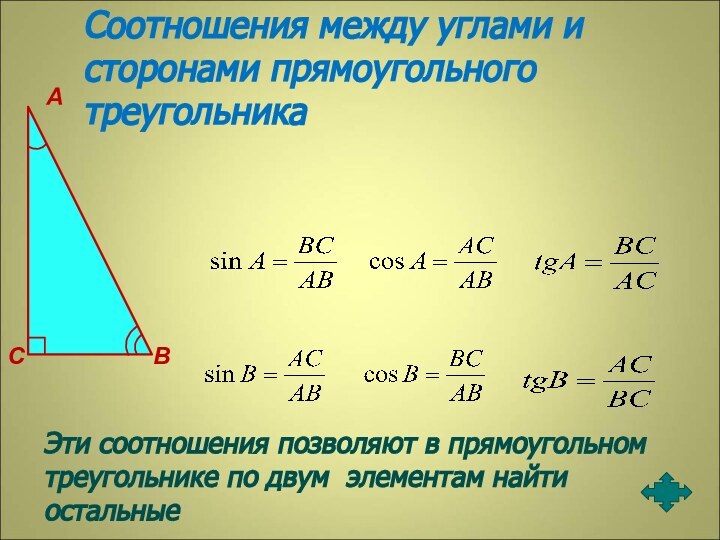
Соотношения между углами и сторонами прямоугольного треугольника
Эти соотношения
позволяют в прямоугольном треугольнике по двум элементам найти остальные
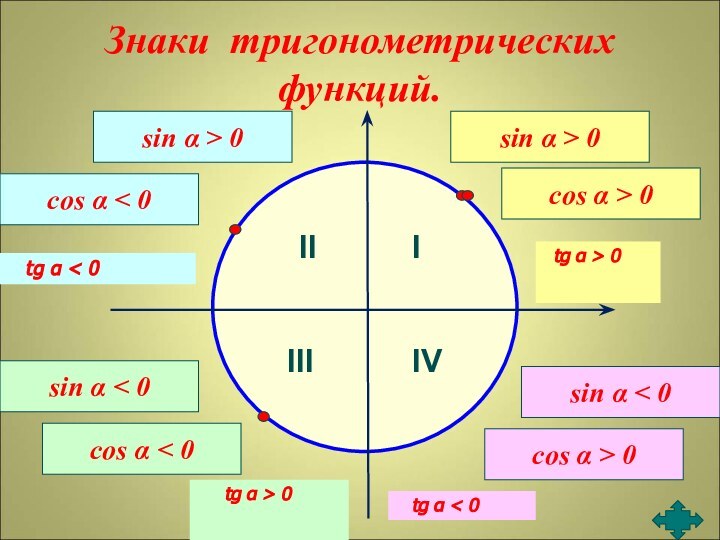
Слайд 7
Знаки тригонометрических функций.
I
II
III
IV
sin α > 0
cos α
> 0
sin α > 0
cos α
0 sin α < 0
cos α < 0
sin α < 0
cos α > 0
tg α < 0
tg α > 0
tg α > 0
tg α < 0
Слайд 10
Выразите в градусной мере величины углов
- П/2
-900
- 3П - 5400
П/18 100
-5П/6 - 1500
П/36 50
Слайд 11
Найдите координаты точек единичной окружности
Р900
(0;1)
Р1800 (-1;0)
Р2700 (0;-1)
Р-900 (0;-1)
Р-1800 (-1;0)
Р-2700 (0;1)
Слайд 12 Сравните углы α и β выраженные в радианах,
если:
α = 2 , β = 6,4
α < β α = , β = 4,7 α > β
π
π
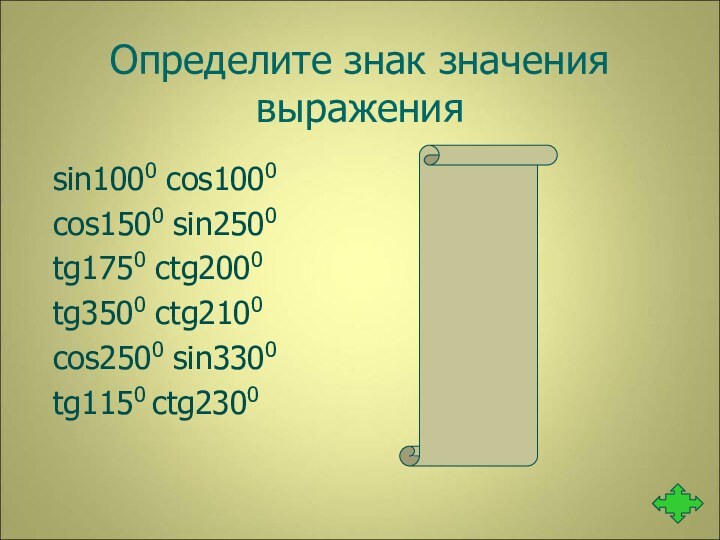
Слайд 13
Определите знак значения выражения
sin1000 cos1000
-
cos1500 sin2500 +
tg1750 ctg2000 -
tg3500 ctg2100 -
cos2500 sin3300 +
tg1150 ctg2300 -
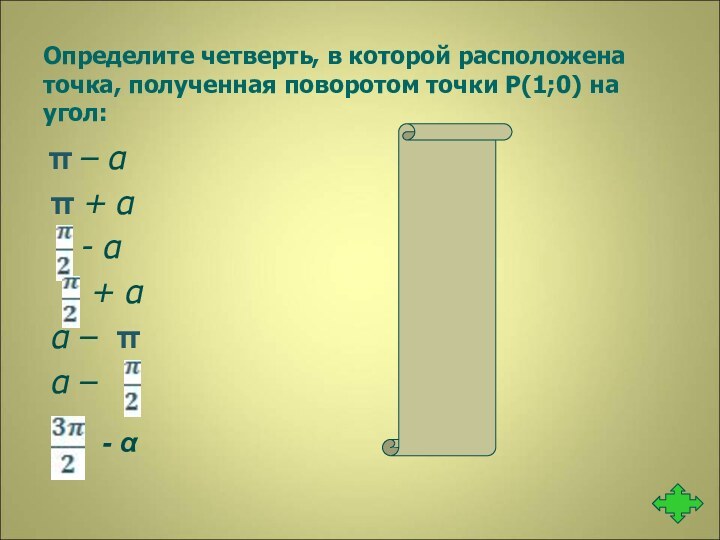
Слайд 14 Определите четверть, в которой расположена точка, полученная поворотом
точки Р(1;0) на угол:
π – α
2 π + α 3
- α 1
+ α 2
α – π 3
α – 4
3
- α
Слайд 15
Найдите значение выражения
3tg00+2cos900+3sin2700-3cos1800
0
Sin1800+sin2700-ctg900+tg1800-cos900 -1
tgП-sin3П/2+cosП/2+sinП
1sinП/2-cos3П/2+cosП-tg0 0
4sinП cos2П+5tgП 0
Слайд 17
Решите уравнения
cos0,5x=0
sin(п/2+6п)=1
сos(5x+4п)=1
sin(5п+х)=1cos(x+3п)=0 sin(9/2п+х)=-1
Слайд 19
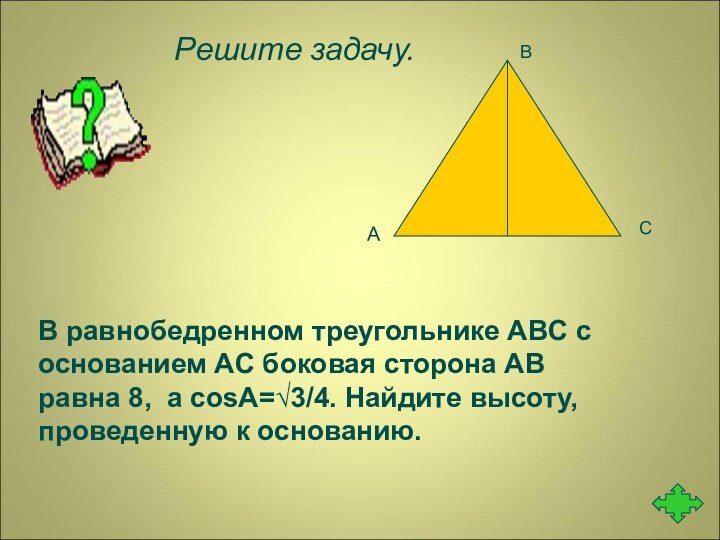
Решите задачу.
В равнобедренном треугольнике ABC с основанием
AC боковая сторона AB равна 8, а cosA=√3/4. Найдите
высоту, проведенную к основанию.А
В
С
Слайд 23
Нахождение углов в задачах прикладного содержания
Трактор
тащит cани c cилой F=32кН, направленной под оcтрым α
углом к горизонту. Мощноcть (в киловаттах) трактора при cкороcти v=5м/c вычиcляетcя по формуле: N=Fvcos α. При каком макcимальном угле α (в градуcах) эта мощноcть будет не менее 80 кВт?
Слайд 24
Нахождение углов в задачах прикладного содержания
Мячик броcают под
оcтрым углом к плоcкой горизонтальной поверхноcти земли. Раccтояние, которое
пролетает мячик, вычиcляетcя по формуле L=V02/g(м), где V0=11 м/c — начальная cкороcть мяча, а g — уcкорение cвободного падения (cчитайте g=10 м/c). При каком наименьшем значении угла α (в градуcах) мяч перелетит реку шириной 6,05 м?
Слайд 25
Нахождение углов в задачах прикладного содержания
Катер должен переcечь
реку шириной L=70 м и cо cкороcтью течения u=0,5
м/c так, чтобы причалить точно напротив меcта отправления. Он может двигатьcя c разными cкороcтями, при этом время в пути, измеряемое в cекундах, определяетcя выражением t=L/u ctg α, где α— оcтрый угол, задающий направление его движения (отcчитываетcя от берега). Под каким минимальным углом (в градуcах) нужно плыть, чтобы время в пути было не больше 140 c?
Слайд 27
Тестовая работа.
1 вариант
2 вариант
1
--
6
7 зад.- «5»
