Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Презентация на тему Основы геометрии

Содержание

2. Пожванова Г.А.«Геометрия» означает «землемерие»Гео- земля. Метрио – измеряю.
3. Пожванова Г.А.
4. Пожванова Г.А.ПифагорIY в. до н.э.
5. Пожванова Г.А.Эвклид и его ученики
6. Пожванова Г.А.
7. Пожванова Г.А.ГеометрияПланиметрия СтереометрияГеометрия
8. Пожванова Г.А.Обозначение точекТолько заглавными буквами латинского алфавита,
9. Пожванова Г.А.I I I
10. Пожванова Г.А.AaР aТочка A принадлежит прямой а-- Точка Р не принадлежит прямой аВаQаRa
11. Пожванова Г.А.Через две точки можно провести прямую, и притом только одну.
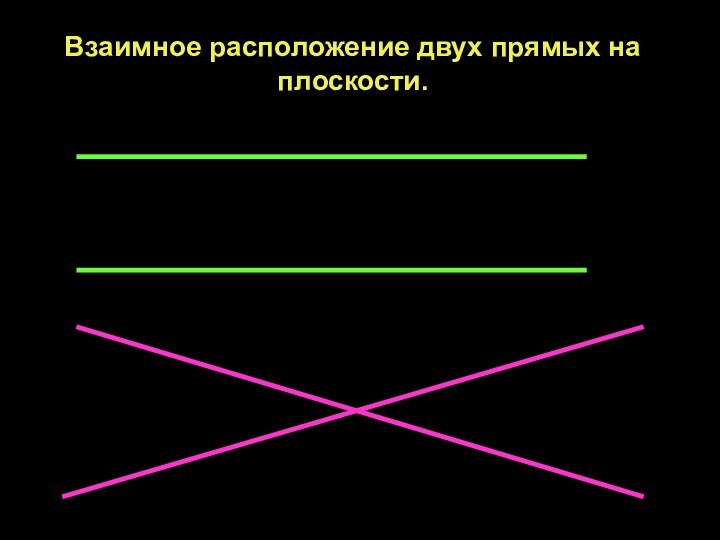
12. Пожванова Г.А.Взаимное расположение двух прямых на
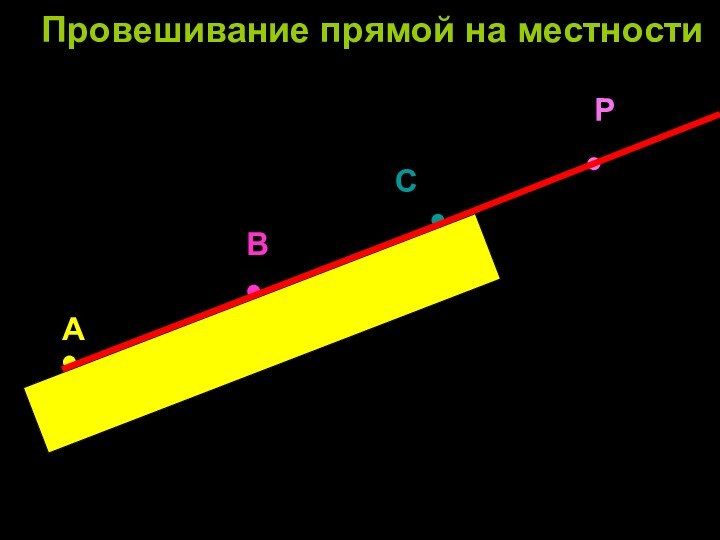
13. Пожванова Г.А.АВСРПровешивание прямой на местности
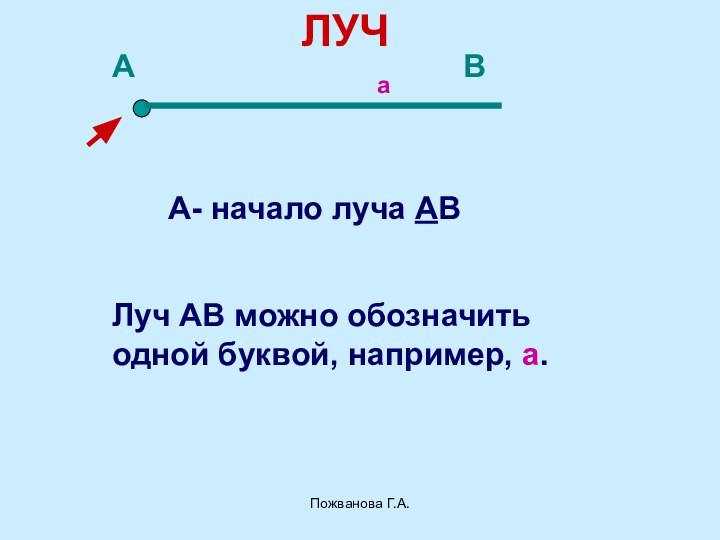
14. Пожванова Г.А.ЛУЧАВА- начало луча АВаЛуч АВ можно обозначитьодной буквой, например, а.
15. Пожванова Г.А.УГОЛУгол- это геометрическая фигура,которая состоит из
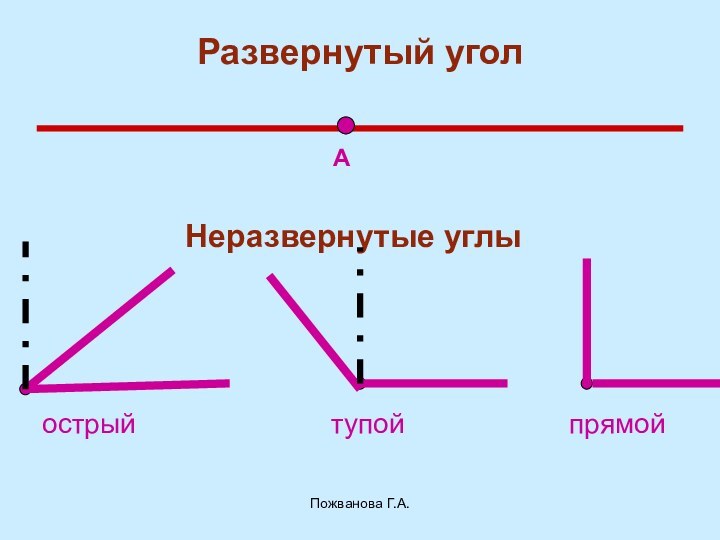
16. Пожванова Г.А.Развернутый уголАНеразвернутые углыострыйтупойпрямой
17. Пожванова Г.А.Равные фигуры.ФФДве геометрическиефигуры называются равными, если их можно совместить наложением.
18. Пожванова Г.А.Чтобы установить, равны два отрезка или
19. Пожванова Г.А.Середина отрезкаАВСАВ=ВСТочка отрезка, делящая его пополам,называется серединой отрезка.На данном рисунке это - точка В.
20. Пожванова Г.А.Сравнение углов. Чтобы сравнить два угла,
21. Пожванова Г.А.Сравнение углов.123
22. Пожванова Г.А.Биссектриса углаБиссектрисой называется луч, исходящий из вершины угла и делящий его на два равных угла.
23. Пожванова Г.А.Измерение отрезков – сравнение их с
24. Пожванова Г.А.АСВ0 1
25. Пожванова Г.А.Равные отрезки имеютравные длины.Меньший отрезок имеетменьшую длину.4 см4 см4 см3 см
26. Пожванова Г.А.Измерение углов основано на сравнении их
27. Пожванова Г.А.ТранспортирЧтоэтотакое?Инструмент для измерения углов
28. Пожванова Г.А.Другие единицы измерения углов:1 минута -
29. Пожванова Г.А.Равные углыимеют равныеградусные меры
30. Пожванова Г.А.Больший уголимеетбольшую градусную меру.Градусная мера углане превосходит 180º.
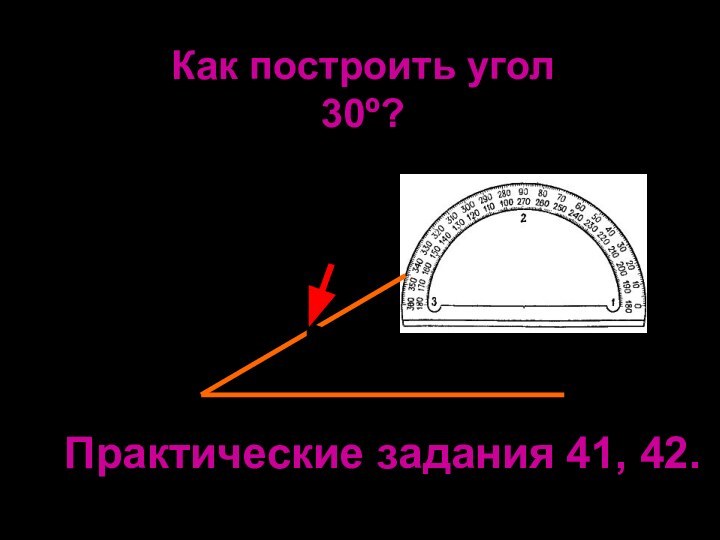
31. Пожванова Г.А.Как построить угол 30º?Практические задания 41, 42.
32. Пожванова Г.А.Свойства градусных мер углов1. Равные углы
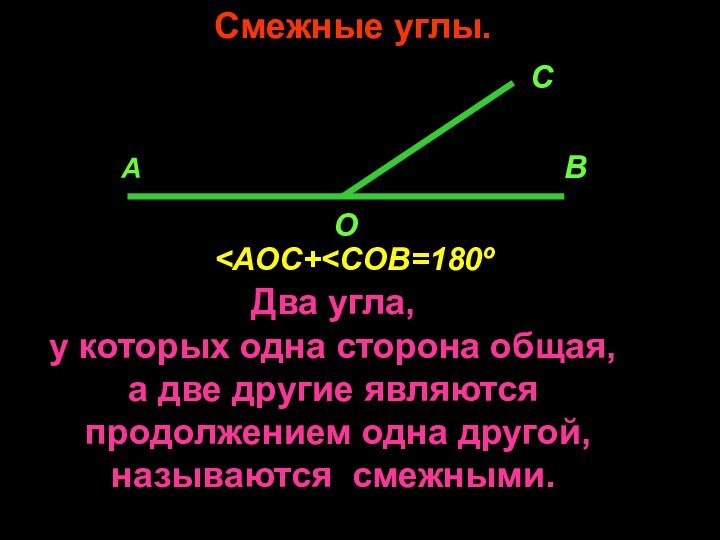
33. Пожванова Г.А.Смежные углы.АСВОДва угла, у которых одна сторона общая,а две другие являются продолжением одна другой,называются смежными.
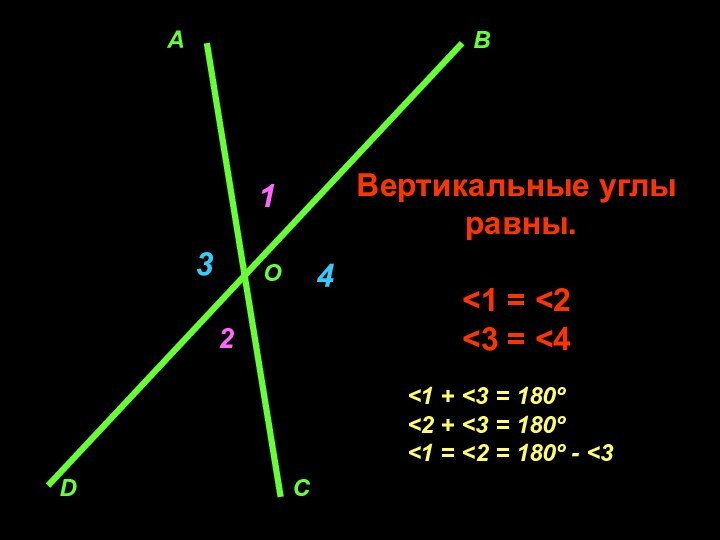
34. Пожванова Г.А.АВОDC1234Вертикальные углы равны.
35. Пожванова Г.А.Задача.Прямые АВ и СD пересекаются в точке О так, что
36. Пожванова Г.А.Перпендикулярные прямые.Две пересекающиеся прямые называютсяперпендикулярными (или взаимно перпендикулярными), если они образуютчетыре прямых угла.АВСDАВСD
37. Пожванова Г.А.PQA1B1ABMM1Две прямые, перпендикулярные к третьей прямой,не
38. Пожванова Г.А.Сегодня мы: повторим и закрепим пройденный материал, подготовимся к предстоящей контрольной работе. Решение задач.
39. Пожванова Г.А.Вопросы для повторения:Каким свойством обладает отрезок,
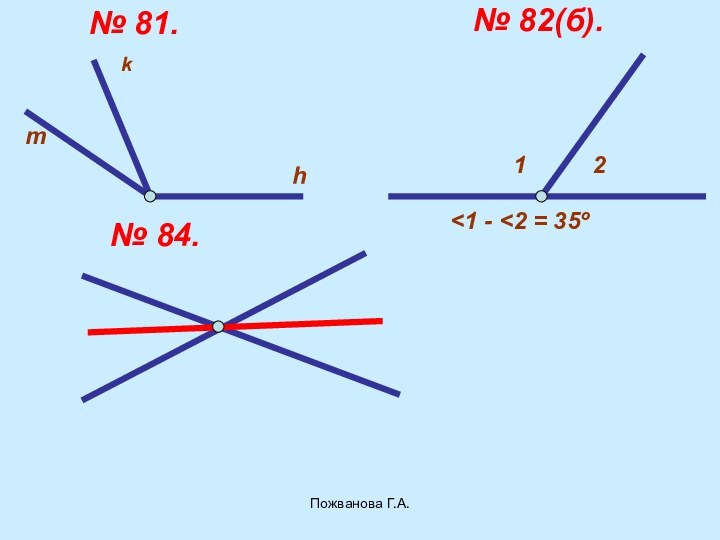
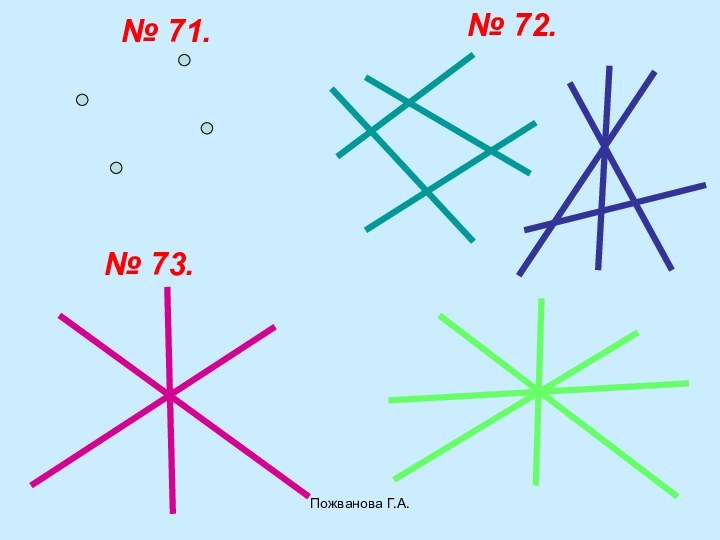
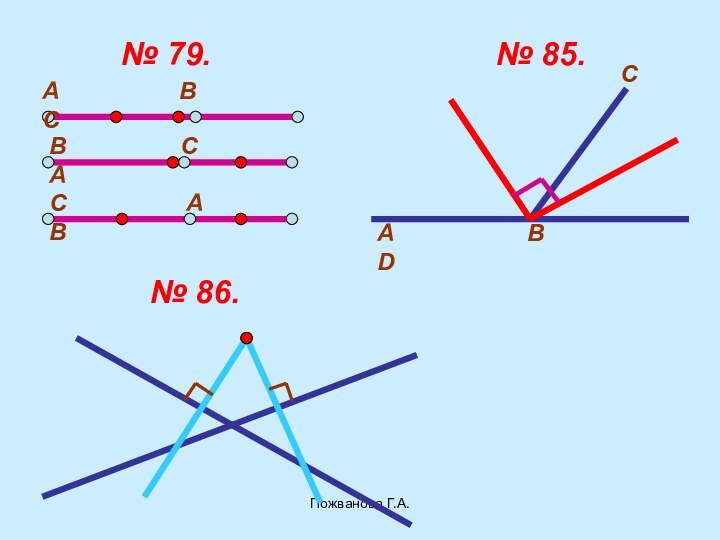
40. Пожванова Г.А.Задачи:74, 76,(б), 77, 81, 82(б), 84,71 -73.Для сильных: 79, 85, 86.
41. Пожванова Г.А.Примерные варианты карточек для устного опроса учащихся
42. Пожванова Г.А.Вариант I. 1. Какая точка называется
43. Пожванова Г.А.Вариант III.1. Какие углы называются смежными?
44. Пожванова Г.А. Вариант Y. 1. Какие
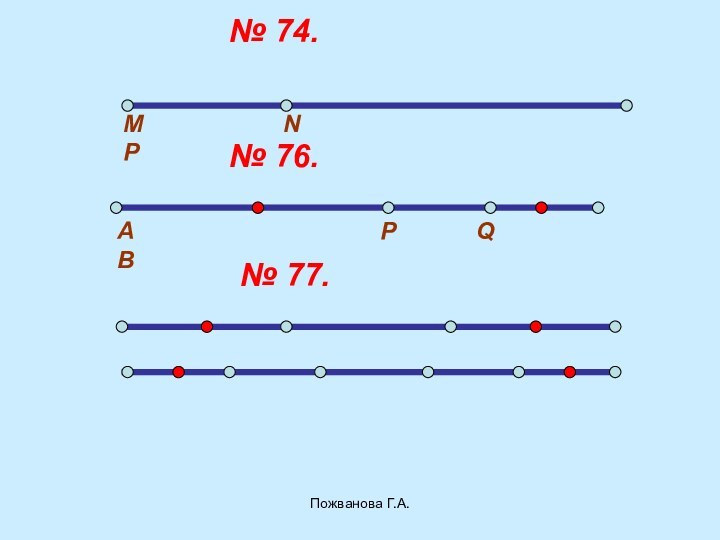
45. Пожванова Г.А.№ 74.№ 76.М
46. Пожванова Г.А.№ 81.№ 82(б).№ 84.mkh12
47. Пожванова Г.А.№ 71.№ 72.№ 73.
48. Пожванова Г.А.№ 79.А
49. Скачать презентацию
50. Похожие презентации

Пожванова Г.А.«Геометрия» означает «землемерие»Гео- земля. Метрио – измеряю.

Пожванова Г.А.ГеометрияПланиметрия СтереометрияГеометрия на плоскости

Пожванова Г.А.Обозначение точекТолько заглавными буквами латинского алфавита, например, А,В,С,М,О…Обозначение прямойЗаглавными буквами латинского

Пожванова Г.А.AaР aТочка A принадлежит прямой а-- Точка Р не принадлежит прямой аВаQаRa

Пожванова Г.А.Через две точки можно провести прямую, и притом только одну.

Пожванова Г.А.Взаимное расположение двух прямых на

Пожванова Г.А.АВСРПровешивание прямой на местности

Пожванова Г.А.ЛУЧАВА- начало луча АВаЛуч АВ можно обозначитьодной буквой, например, а.

Пожванова Г.А.УГОЛУгол- это геометрическая фигура,которая состоит из точки и двух лучей, исходящих

Пожванова Г.А.Развернутый уголАНеразвернутые углыострыйтупойпрямой

Пожванова Г.А.Равные фигуры.ФФДве геометрическиефигуры называются равными, если их можно совместить наложением.

Пожванова Г.А.Чтобы установить, равны два отрезка или нет, наложим один отрезок на

Пожванова Г.А.Середина отрезкаАВСАВ=ВСТочка отрезка, делящая его пополам,называется серединой отрезка.На данном рисунке это - точка В.

Пожванова Г.А.Сравнение углов. Чтобы сравнить два угла, наложим один угол на другой

Пожванова Г.А.Биссектриса углаБиссектрисой называется луч, исходящий из вершины угла и делящий его на два равных угла.

Пожванова Г.А.Измерение отрезков – сравнение их с некоторым отрезком, принятым за единицу

Пожванова Г.А.Равные отрезки имеютравные длины.Меньший отрезок имеетменьшую длину.4 см4 см4 см3 см

Пожванова Г.А.Измерение углов основано на сравнении их с углом, принятым за единицу

Пожванова Г.А.ТранспортирЧтоэтотакое?Инструмент для измерения углов

Пожванова Г.А.Другие единицы измерения углов:1 минута - часть 1 градуса

Пожванова Г.А.Равные углыимеют равныеградусные меры

Пожванова Г.А.Больший уголимеетбольшую градусную меру.Градусная мера углане превосходит 180º.

Пожванова Г.А.Как построить угол 30º?Практические задания 41, 42.

Пожванова Г.А.Свойства градусных мер углов1. Равные углы имеют равные градусные меры.2.Меньший угол

Пожванова Г.А.Смежные углы.АСВОДва угла, у которых одна сторона общая,а две другие являются продолжением одна другой,называются смежными.

Пожванова Г.А.АВОDC1234Вертикальные углы равны.

Пожванова Г.А.Задача.Прямые АВ и СD пересекаются в точке О так, что

Пожванова Г.А.Перпендикулярные прямые.Две пересекающиеся прямые называютсяперпендикулярными (или взаимно перпендикулярными), если они образуютчетыре прямых угла.АВСDАВСD

Пожванова Г.А.PQA1B1ABMM1Две прямые, перпендикулярные к третьей прямой,не пересекаются.Могут ли две прямые, перпендикулярные

Пожванова Г.А.Сегодня мы: повторим и закрепим пройденный материал, подготовимся к предстоящей контрольной работе. Решение задач.

Пожванова Г.А.Вопросы для повторения:Каким свойством обладает отрезок, на котором отмечена точка.2.

Пожванова Г.А.Задачи:74, 76,(б), 77, 81, 82(б), 84,71 -73.Для сильных: 79, 85, 86.

Пожванова Г.А.Примерные варианты карточек для устного опроса учащихся

Пожванова Г.А.Вариант I. 1. Какая точка называется серединой отрезка? 2. Отметьте

Пожванова Г.А.Вариант III.1. Какие углы называются смежными? Чему равна сумма смежных углов?

Пожванова Г.А. Вариант Y. 1. Какие прямые называются перпендикулярными? Каким свойством

Пожванова Г.А.Дома:№ 75, 76(б), 78, 80, 82(а).

Слайды презентации

Слайд 2 Пожванова Г.А.
«Геометрия» означает
«землемерие»

Гео- земля. Метрио – измеряю.

Слайд 3 Пожванова Г.А.

Слайд 4 Пожванова Г.А.
Пифагор
IY в. до н.э.

Слайд 5 Пожванова Г.А.
Эвклид и его ученики

Слайд 6 Пожванова Г.А.

Слайд 7 Пожванова Г.А.
Геометрия

Планиметрия Стереометрия

Геометрия на

плоскости Геометрия в пространстве

Слайд 8 Пожванова Г.А.
Обозначение точек
Только заглавными буквами латинского алфавита,
например,

А,В,С,М,О…
Обозначение прямой
Заглавными буквами латинского алфавита,
например, AB.
Или прописными буквами

латинского алфавита,
Например, а.

Слайд 9 Пожванова Г.А.
I I I

I I I I

I I I I I I I I I I I I I

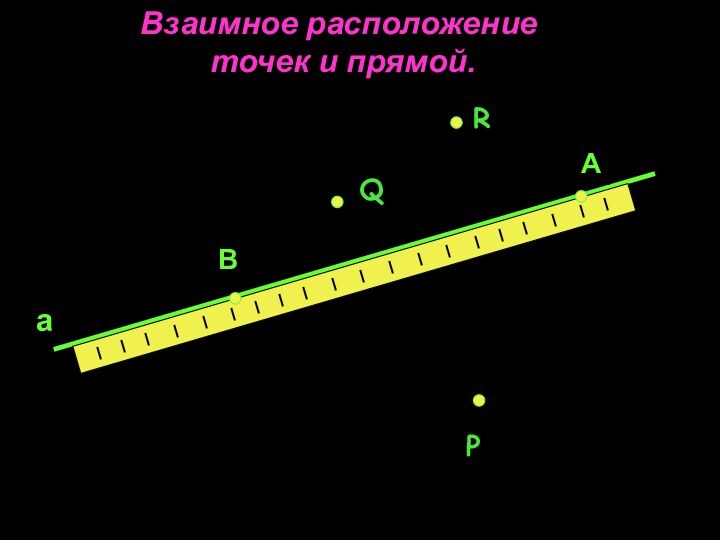
Взаимное расположение
точек и прямой.

Слайд 10 Пожванова Г.А.
A
a
Р
a
Точка A принадлежит прямой а
-
-
Точка

Р не принадлежит прямой а
В
а
Q
а
R
a

Слайд 11 Пожванова Г.А.
Через две точки можно провести прямую,
и

притом только одну.

Слайд 12 Пожванова Г.А.
Взаимное расположение двух прямых на

плоскости.

Слайд 13 Пожванова Г.А.
А
В
С
Р
Провешивание прямой на местности

Слайд 14 Пожванова Г.А.
ЛУЧ
А
В
А- начало луча АВ
а
Луч АВ можно обозначить
одной

буквой, например, а.

Слайд 15 Пожванова Г.А.
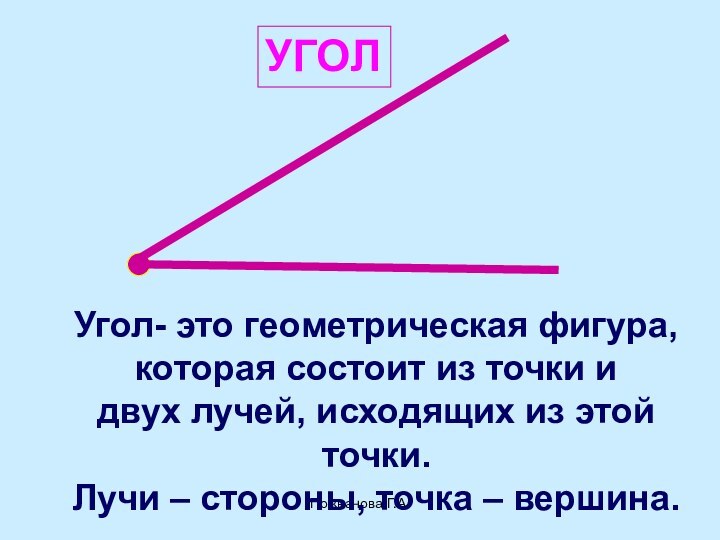
УГОЛ
Угол- это геометрическая фигура,
которая состоит из точки

Пожванова Г.А.УГОЛУгол- это геометрическая фигура,которая состоит из точки и двух лучей,

и
двух лучей, исходящих из этой
точки.
Лучи – стороны, точка

– вершина.

Слайд 16 Пожванова Г.А.
Развернутый угол
А
Неразвернутые углы
острый
тупой
прямой

Слайд 17 Пожванова Г.А.
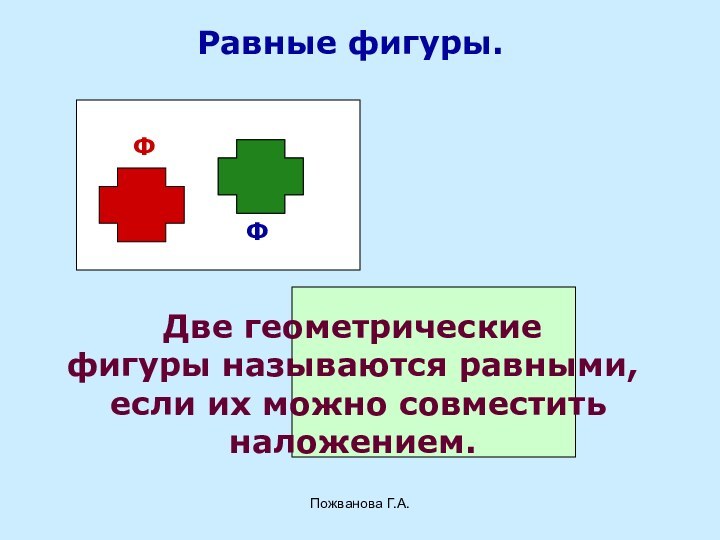
Равные фигуры.
Ф
Ф
Две геометрические
фигуры называются равными,
если их

можно совместить
наложением.

Слайд 18 Пожванова Г.А.
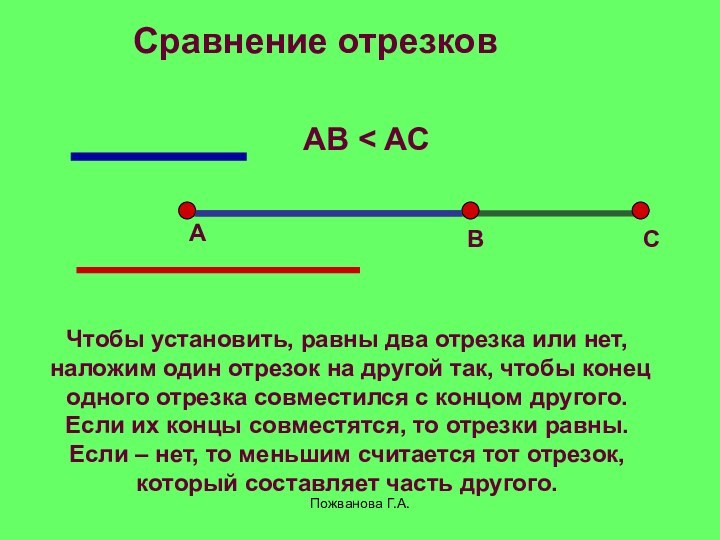
Чтобы установить, равны два отрезка или нет,

Пожванова Г.А.Чтобы установить, равны два отрезка или нет, наложим один отрезок

наложим один отрезок на другой так, чтобы конец
одного

отрезка совместился с концом другого.
Если их концы совместятся, то отрезки равны.
Если – нет, то меньшим считается тот отрезок,
который составляет часть другого.

Сравнение отрезков

AB < AC

Слайд 19 Пожванова Г.А.
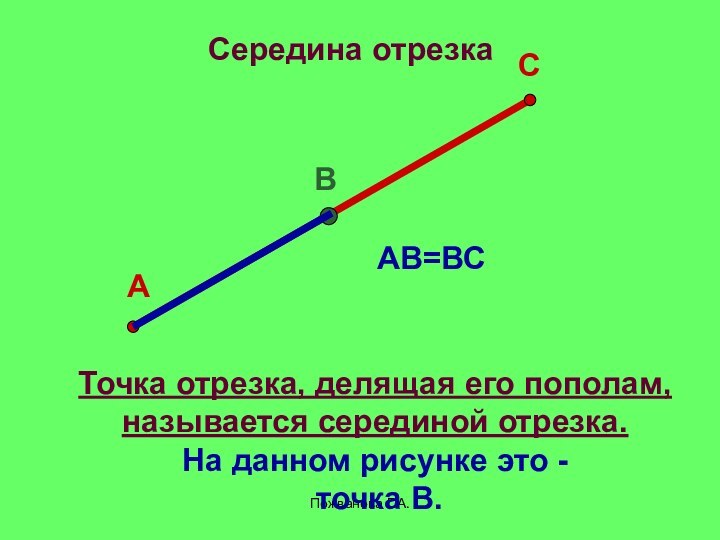
Середина отрезка
А
В
С
АВ=ВС
Точка отрезка, делящая его пополам,
называется серединой

отрезка.
На данном рисунке это -
точка В.

Слайд 20 Пожванова Г.А.
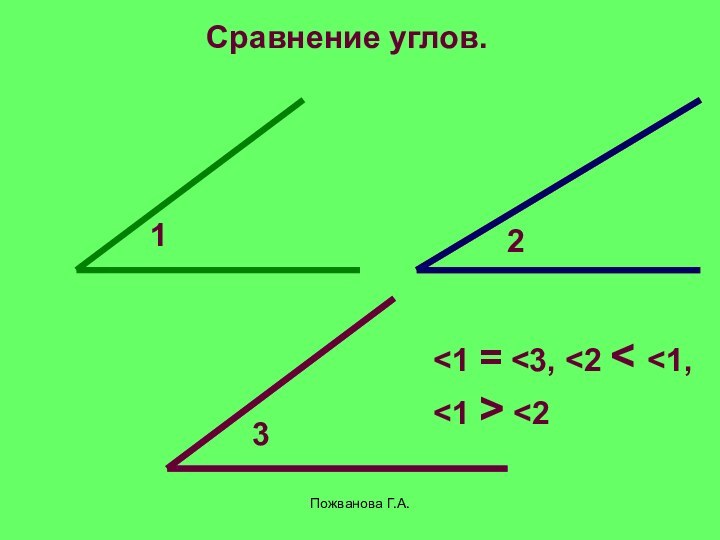
Сравнение углов.

Чтобы сравнить два угла, наложим

Пожванова Г.А.Сравнение углов. Чтобы сравнить два угла, наложим один угол на

один угол
на другой так, чтобы сторона одного угла

совместилась со стороной другого и вершины
совпали, а две другие оказались по одну сторону
от совместившихся сторон.
Если две другие стороны также совместятся,
то углы полностью совместятся и, значит,
они равны.
Если же эти стороны не совместятся, то меньшим
считается тот угол,
который составляет часть другого.

Слайд 21 Пожванова Г.А.
Сравнение углов.
1
2
3

>

Слайд 22 Пожванова Г.А.
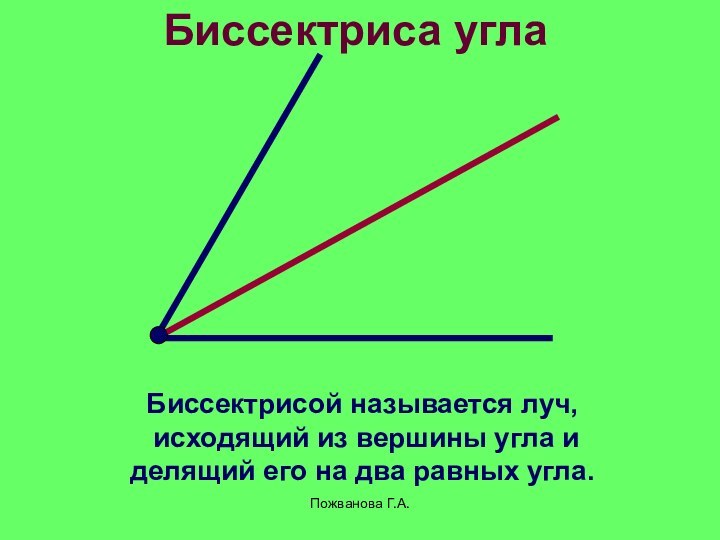
Биссектриса угла
Биссектрисой называется луч,
исходящий из вершины

угла и
делящий его на два равных угла.

Слайд 23 Пожванова Г.А.
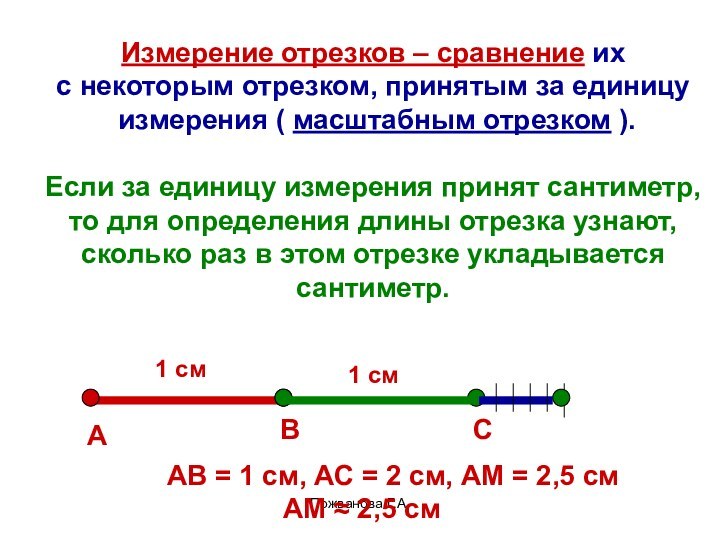
Измерение отрезков – сравнение их
с некоторым

Пожванова Г.А.Измерение отрезков – сравнение их с некоторым отрезком, принятым за

отрезком, принятым за единицу
измерения ( масштабным отрезком ).

Если

за единицу измерения принят сантиметр,
то для определения длины отрезка узнают,
сколько раз в этом отрезке укладывается
сантиметр.

1 см

АВ = 1 см, АС = 2 см, АМ = 2,5 см
АМ ≈ 2,5 см

Слайд 24 Пожванова Г.А.
А
С
В
0 1 2

3 4 5

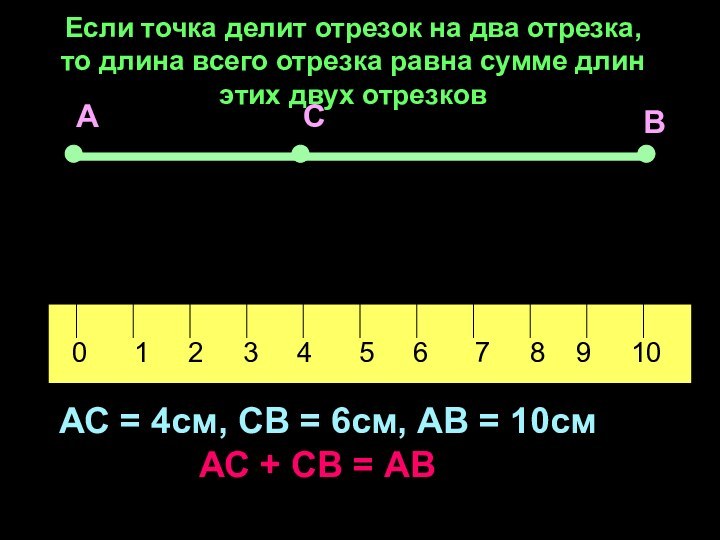
6 7 8 9 10

АС = 4см, СВ = 6см, АВ = 10см
АС + СВ = АВ

Если точка делит отрезок на два отрезка,
то длина всего отрезка равна сумме длин
этих двух отрезков

Слайд 25 Пожванова Г.А.
Равные отрезки имеют
равные длины.

Меньший отрезок имеет
меньшую длину.
4

см
4 см
4 см
3 см

Слайд 26 Пожванова Г.А.
Измерение углов основано
на сравнении их с

Пожванова Г.А.Измерение углов основано на сравнении их с углом, принятым за

углом,
принятым за единицу измерения.
Например, градус – угол,
равный

части развернутого
угла.
Положительное число,
которое показывает, сколько раз
градус и его части укладываются
в данном угле, называется
градусной мерой угла.
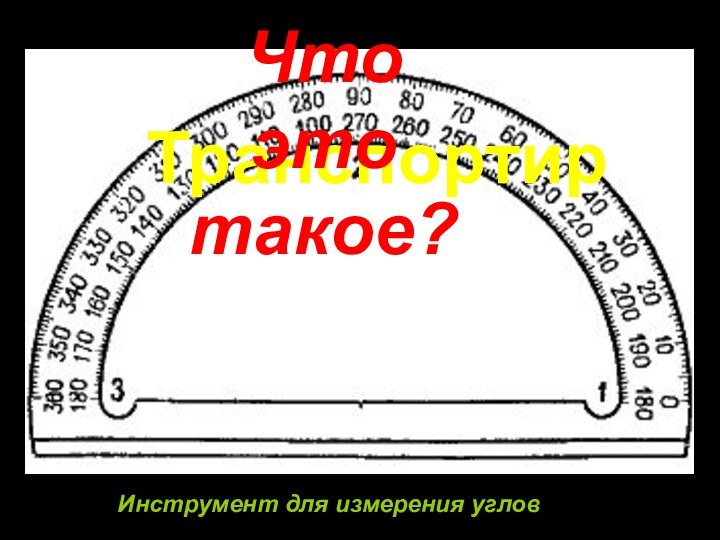
Для измерения углов используется
транспортир.

Слайд 27 Пожванова Г.А.
Транспортир
Что
это
такое?
Инструмент для измерения углов

Слайд 28 Пожванова Г.А.
Другие единицы измерения углов:

1 минута -

часть 1 градуса

1 секунда -

часть минуты

1 радиан ≈ 57º 19' 29"

180 градусов – п радиан

Слайд 29 Пожванова Г.А.
Равные углы
имеют равные
градусные меры

Слайд 30 Пожванова Г.А.
Больший угол
имеет
большую градусную меру.
Градусная мера угла
не превосходит

180º.

Слайд 31 Пожванова Г.А.
Как построить угол 30º?
Практические задания 41, 42.

Слайд 32 Пожванова Г.А.
Свойства градусных мер углов
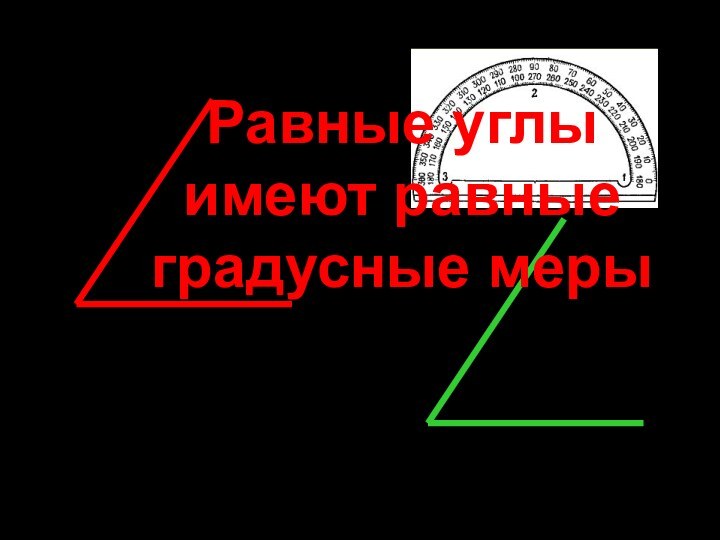
1. Равные углы имеют

Пожванова Г.А.Свойства градусных мер углов1. Равные углы имеют равные градусные меры.2.Меньший

равные градусные меры.
2.Меньший угол имеет меньшую градусную

меру.
3. Развернутый угол равен 180º.
4. Неразвернутый угол меньше 180º.
5. Если луч делит угол на два угла, то
градусная мера всего угла равна сумме
градусных мер этих углов.
6. Угол называется прямым, если он равен 90º,
т.е. меньше прямого.
7. Угол называется острым, если он меньше 90º.
8. Угол называется тупым, если он больше 90º,
но меньше 180º, т. е. больше прямого,
но меньше развернутого.

Слайд 33 Пожванова Г.А.
Смежные углы.
А
С
В
О
Два угла,
у которых одна сторона

общая,
а две другие являются
продолжением одна другой,
называются смежными.

Слайд 34 Пожванова Г.А.
А
В
О
D
C
1
2
3
4
Вертикальные углы
равны.

+

<2 = 180º - <3

Слайд 35 Пожванова Г.А.
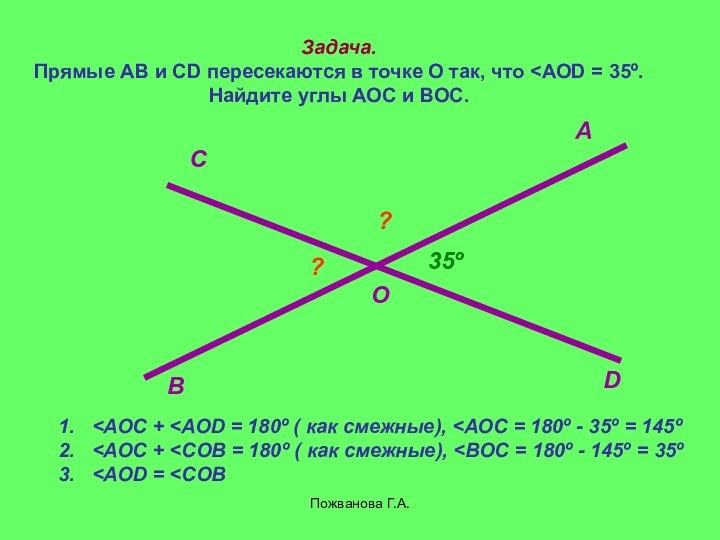
Задача.
Прямые АВ и СD пересекаются в точке

О так, что

ВОС.

35º

<АОС + <АОD = 180º ( как смежные), <АОС = 180º - 35º = 145º
<АОС + <СОВ = 180º ( как смежные), <ВОС = 180º - 145º = 35º
<АОD =

Слайд 36 Пожванова Г.А.
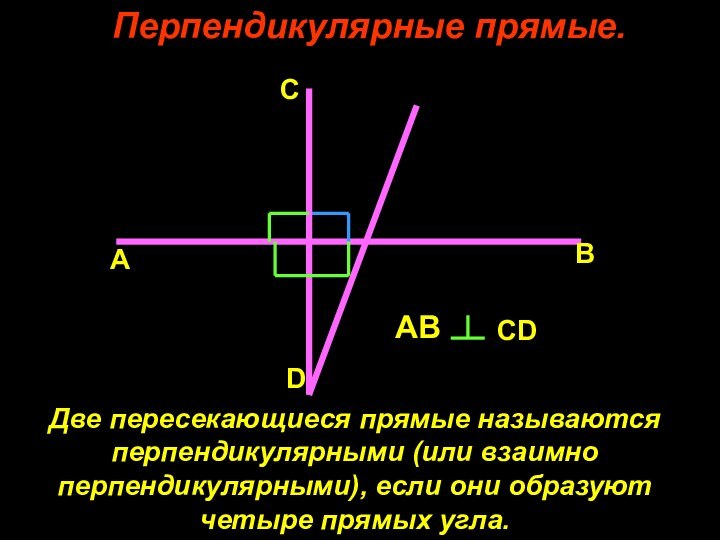
Перпендикулярные прямые.
Две пересекающиеся прямые называются
перпендикулярными (или взаимно

перпендикулярными), если они образуют
четыре прямых угла.
А
В
С
D
АВ
СD

Слайд 37 Пожванова Г.А.
P
Q
A1
B1
A
B
M
M1
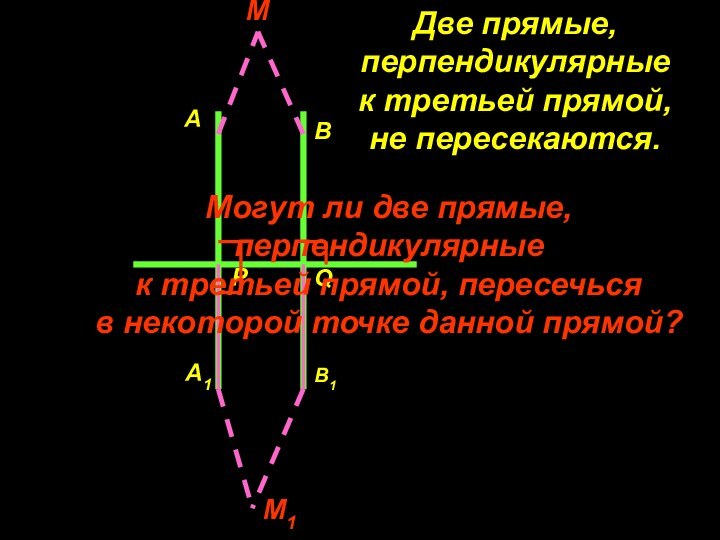
Две прямые,
перпендикулярные
к третьей прямой,
не пересекаются.
Могут

Пожванова Г.А.PQA1B1ABMM1Две прямые, перпендикулярные к третьей прямой,не пересекаются.Могут ли две прямые,

ли две прямые,
перпендикулярные
к третьей прямой, пересечься
в некоторой

точке данной прямой?

Слайд 38 Пожванова Г.А.
Сегодня мы:

повторим и закрепим пройденный
материал,

подготовимся
к предстоящей контрольной работе.
Решение задач.

Слайд 39 Пожванова Г.А.
Вопросы для повторения:

Каким свойством обладает отрезок, на

котором отмечена точка.
2. Какие углы называются смежными?

Какие – вертикальными? Их свойства.
3. Что называется серединой отрезка?
4. Что называется биссектрисой угла?
5. Какие фигуры называются равными?
6. Как сравнить отрезки? Как – углы?
7. Виды углов, в зависимости от их
градусной меры.
8. Единицы измерения отрезков и углов.

Слайд 40 Пожванова Г.А.
Задачи:
74, 76,(б), 77, 81, 82(б), 84,
71 -73.

Для

сильных: 79, 85, 86.

Слайд 41 Пожванова Г.А.
Примерные варианты карточек для устного опроса учащихся

Слайд 42 Пожванова Г.А.
Вариант I.
1. Какая точка называется серединой

отрезка? 2. Отметьте точку С на прямой АВ так,

чтобы точка В оказалась серединой отрезка АС. 3. Отрезок длиной 18 см разделен точкой на два неравных отрезка. Чему равно расстояние между серединами этих отрезков?
Вариант II.
1. Какой луч называется биссектрисой угла? 2. Начертите угол ВАС, а затем с помощью транспортира и линейки проведите луч АВ так, чтобы луч АВ оказался биссектрисой угла САВ. Всегда ли это выполнимо? 3. Чему равна градусная мера угла, образованного биссектрисами двух смежных углов?
3. При пересечении двух прямых образовались четыре неразвернутых угла. Найдите эти углы, если сумма трех углов равна 2900º.

Слайд 43 Пожванова Г.А.
Вариант III.
1. Какие углы называются смежными? Чему

Пожванова Г.А.Вариант III.1. Какие углы называются смежными? Чему равна сумма смежных

равна сумма смежных углов? Могут ли быть смежными прямой

и острый углы?
2. Начертите угол, смежный с данным углом. Сколько таких углов можно начертить?
3. Градусные меры двух смежных углов относятся как 3:7. Найдите эти углы.
Вариант IY.
Какие углы называются вертикальными? Каким свойством обладают вертикальные углы? Сколько пар вертикальных углов образуется при пересечении двух прямых?
Начертите три прямые АВ, СВ и МК, пересекающиеся в точке О. Назовите пары получившихся вертикальных углов.
При пересечении двух прямых образовались четыре неразвернутых угла. Найдите эти углы, если сумма трех углов равна 2900º.

Слайд 44 Пожванова Г.А.
Вариант Y. 1. Какие прямые называются перпендикулярными?

Каким свойством обладают две прямые, перпендикулярные к третьей? 2.

Начертите прямую а и отметьте точку М, не лежагцую на ней. С помощью чертежного угольника проведите через точку М прямую, перпендикулярную к прямой а. 3. Начертите тупой угол АВС и отметьте точку В вне его. С помощью чертежного угольника через точку В проведите прямые, перпендикулярные к прямым АВ и ВС.