- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Параллельное проектирование
Содержание
- 2. В стереометрии изучаются пространственные фигуры, однако на
- 3. Точка А` является параллельной проекцией точки А
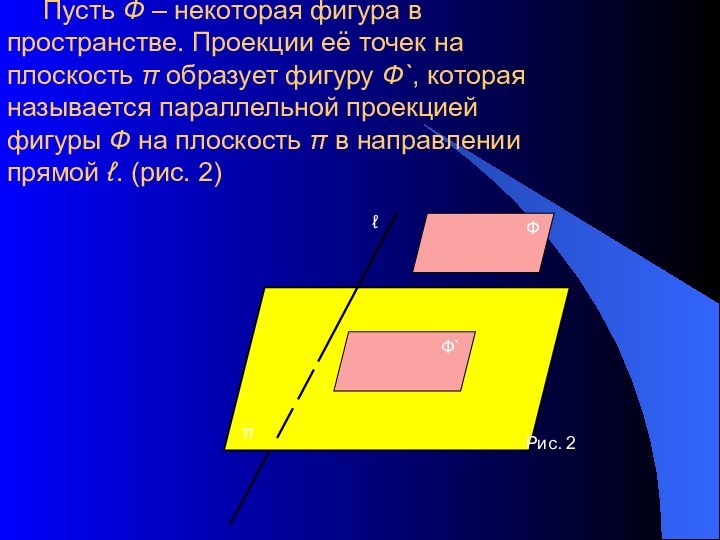
- 4. Пусть Ф – некоторая фигура в пространстве.
- 5. Свойство №1. Если прямая параллельна или совпадает
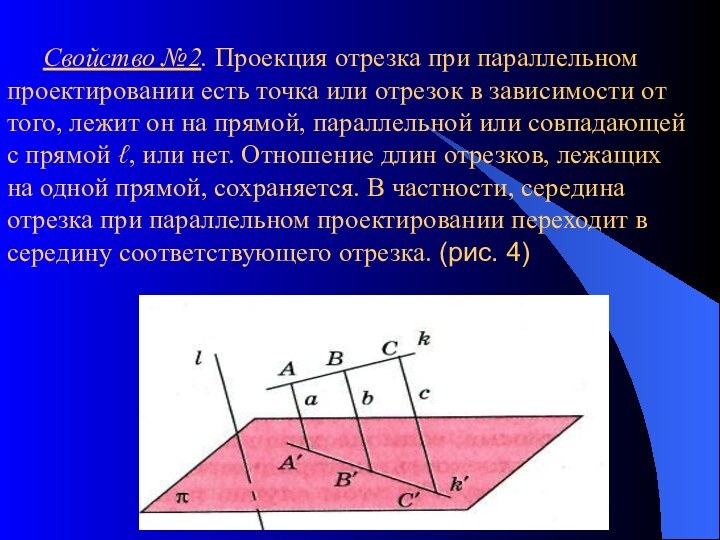
- 6. Свойство №2. Проекция отрезка при параллельном проектировании
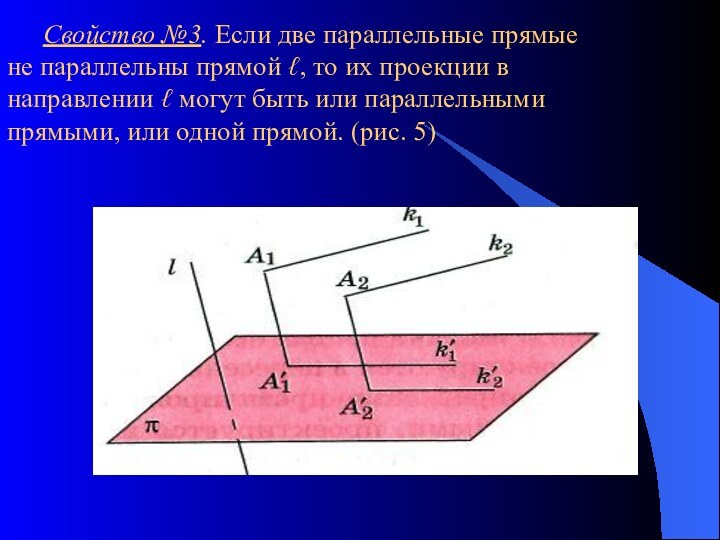
- 7. Свойство №3. Если две параллельные прямые не
- 8. Пример №1. Как должны быть расположены две
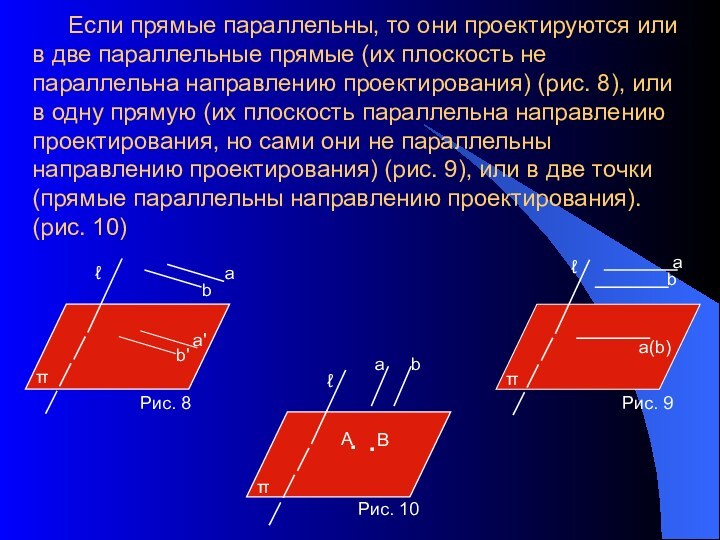
- 9. Если прямые параллельны, то они проектируются или
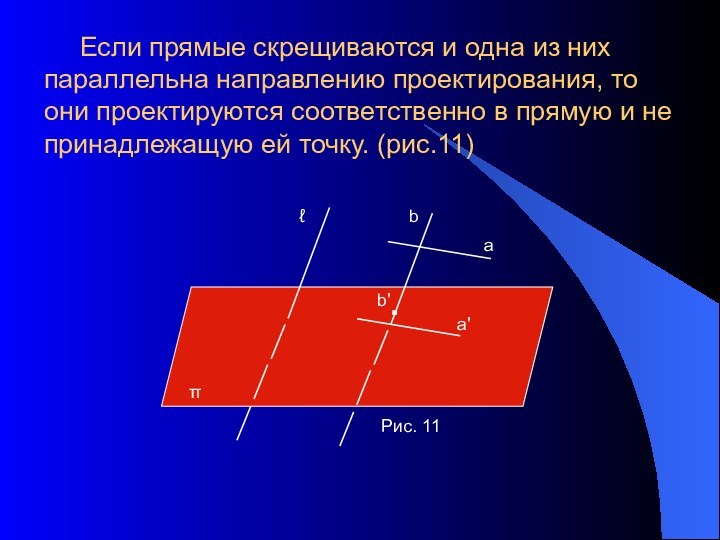
- 10. Если прямые скрещиваются и одна из них
- 11. Пример № 2. Отрезок АВ, равный а,
- 12. Скачать презентацию
- 13. Похожие презентации
В стереометрии изучаются пространственные фигуры, однако на чертеже они изображаются в виде плоских фигур. Каким же образом следует изображать пространственную фигуру на плоскости? Обычно для этого используется параллельное проектирование пространственной фигуры на плоскость.