Презентация на тему Плоскости в пространстве

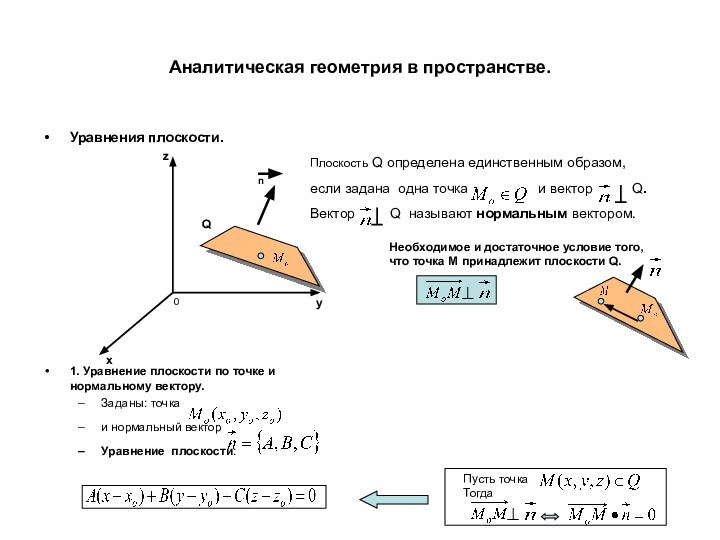
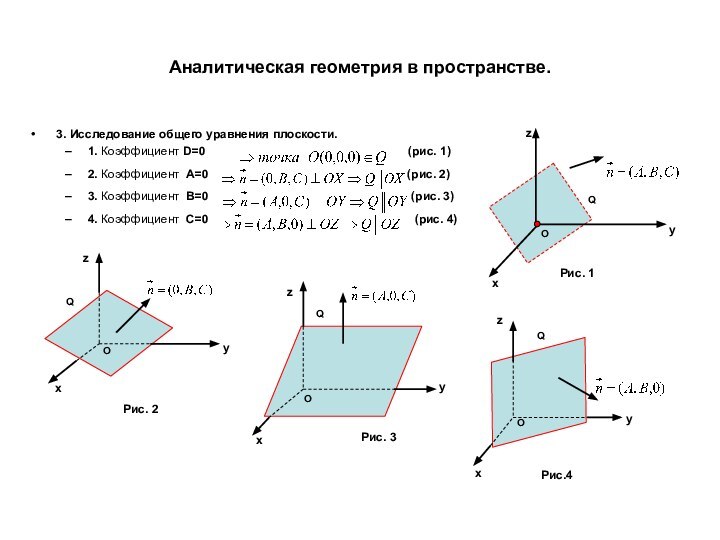
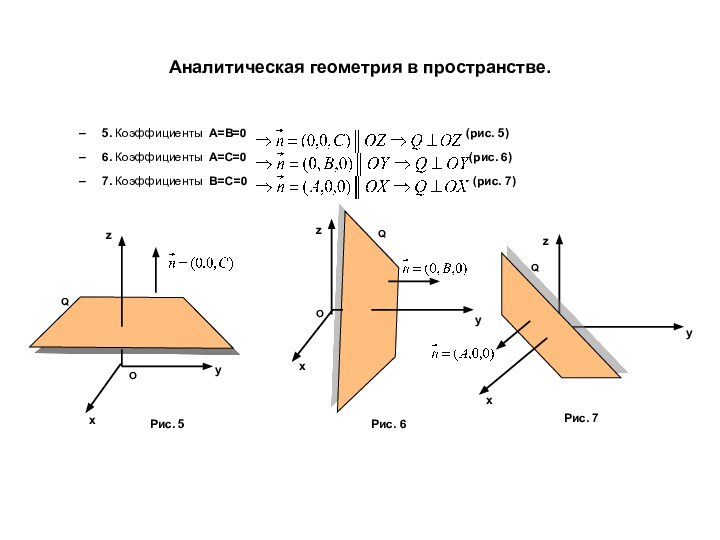
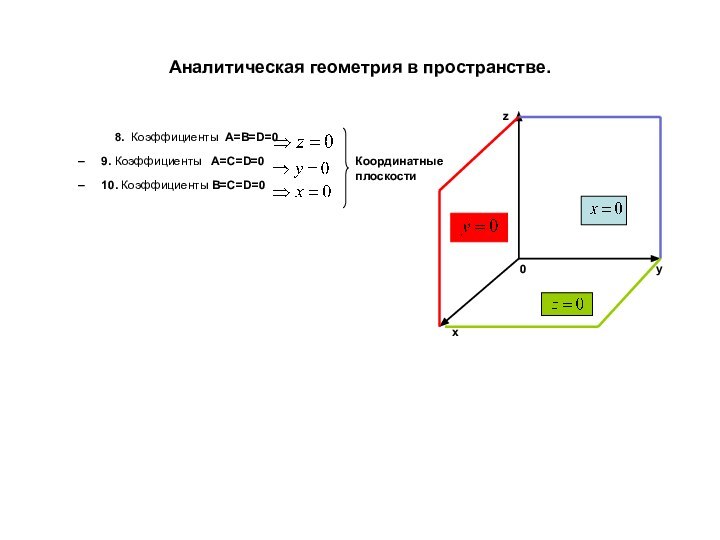
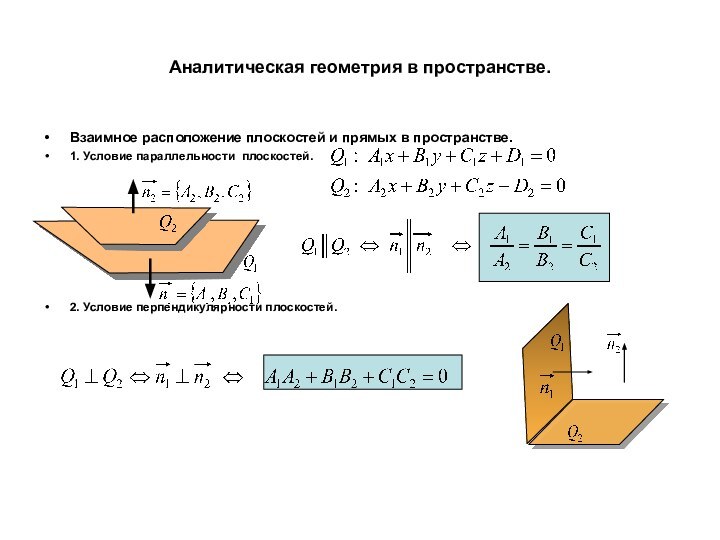
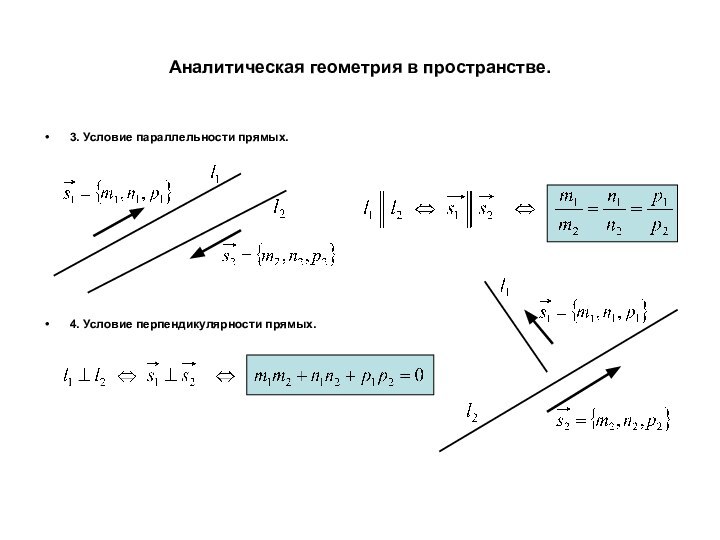
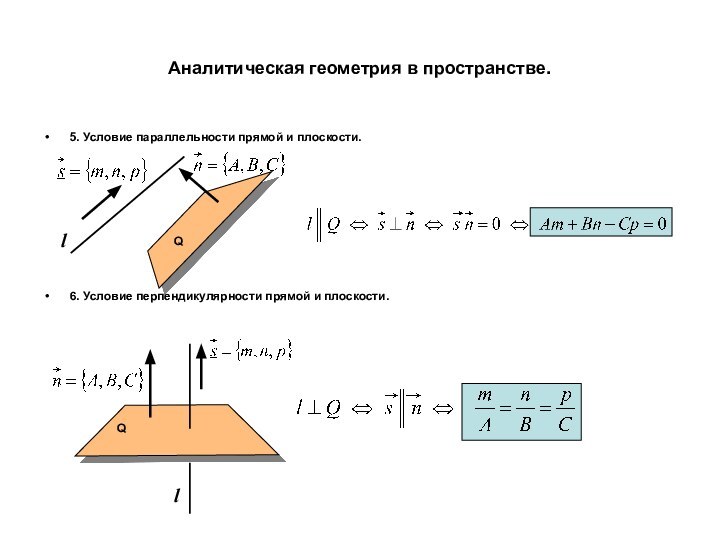
точке и нормальному вектору.
Заданы: точка
и нормальный вектор
Уравнение плоскости:
0
х
y
z
Q
n
Плоскость

Необходимое и достаточное условие того,
что точка М принадлежит плоскости Q.

Пусть точка
Тогда

общим уравнением плоскости.
Коэффициенты A,B,C в уравнении определяют координаты нормального

Теорема.
Всякое уравнение первой степени
с тремя переменными x,y,z вида
(1)

задает плоскость в пространстве
и наоборот, всякая плоскость
в пространстве может быть задана
уравнением с тремя переменными x,y,z
вида (1).

Q

Q

Коэффициент D=0

x

y

z

O

x

y

z

O

x

y

z

O

x

y

z

O

Рис. 1

Рис. 2

Рис. 3

Рис.4

Q

Q

Q

Q

x

y

z

O

x

y

z

O

x

y

z

O

Q

Q

Q

Рис. 5

Рис. 6

Рис. 7

A=C=D=0
10. Коэффициенты B=C=D=0
x
y
z
0
Координатные
плоскости

уравнение прямой.
Аксиома: линия пересечения двух плоскостей – прямая.
l
l :
(2)
Теорема.
Система

Система уравнений (2) называется общим уравнением прямой.

уравнения прямой.
l
l :
Пусть точка
Тогда

в пространстве.
1. Условие параллельности плоскостей.








2. Условие перпендикулярности плоскостей.

перпендикулярности прямых.