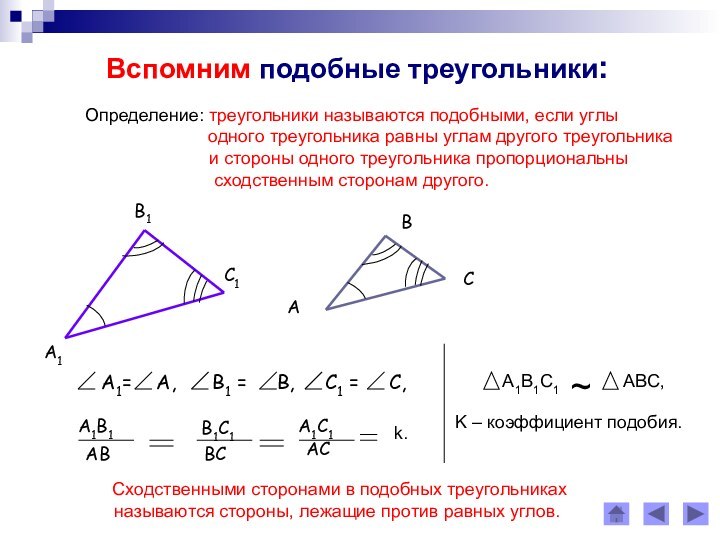
одного треугольника равны углам другого треугольника
и стороны одного треугольника пропорциональны
сходственным сторонам другого.
Сходственными сторонами в подобных треугольниках
называются стороны, лежащие против равных углов.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть
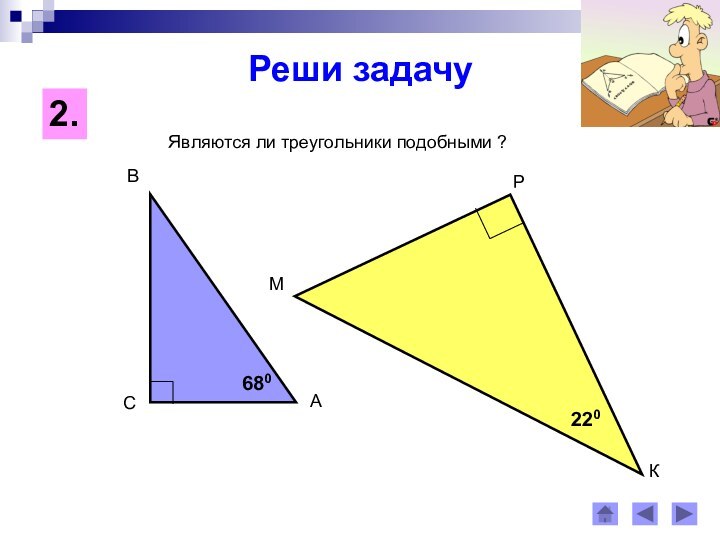
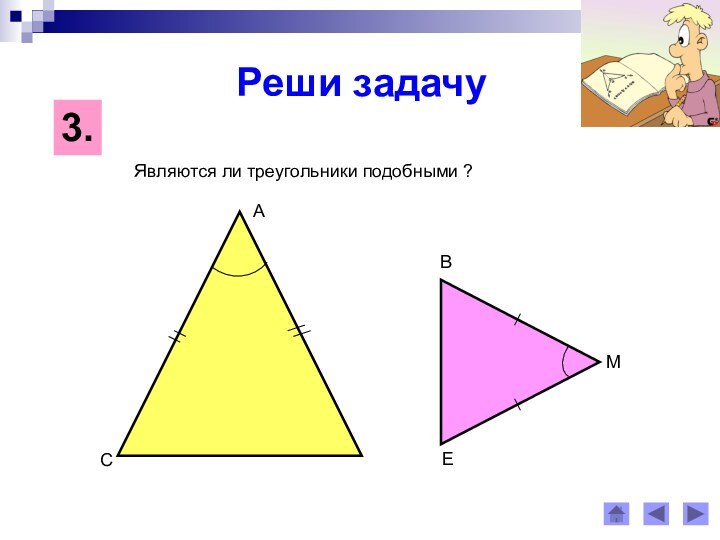
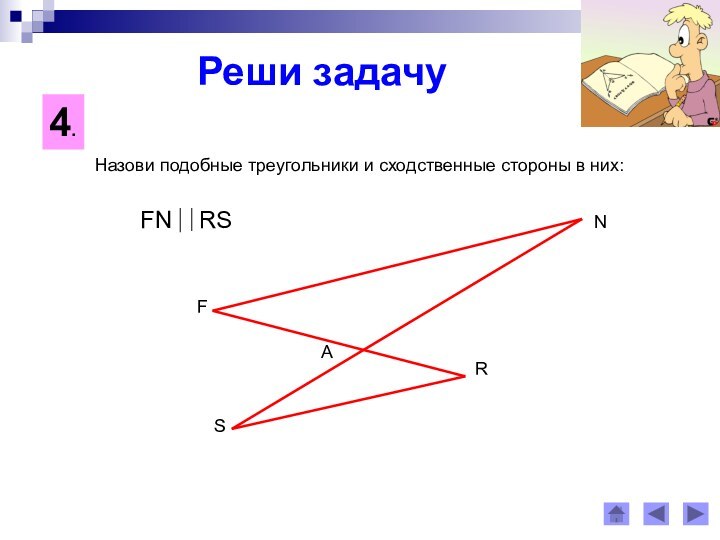
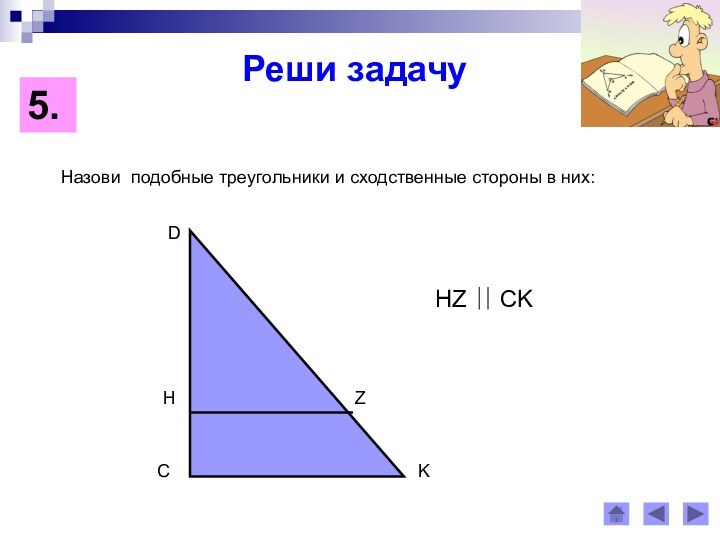
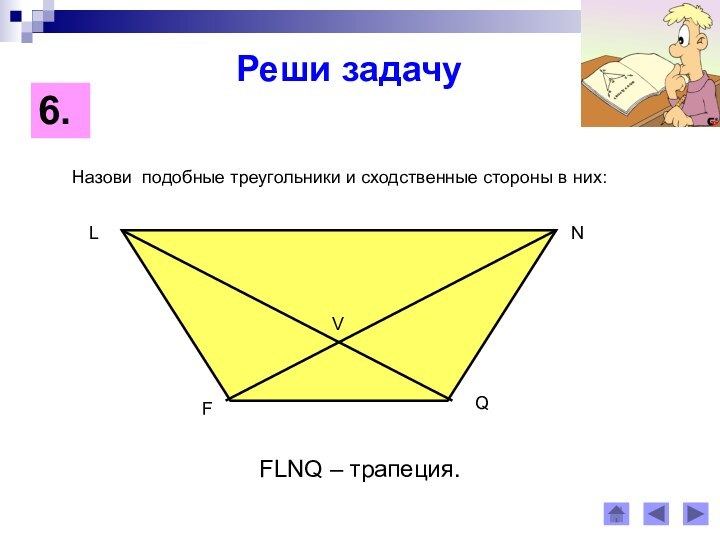
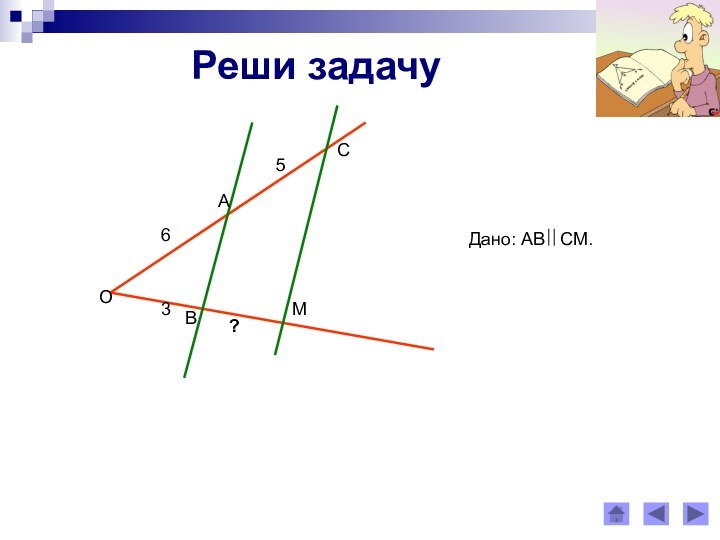
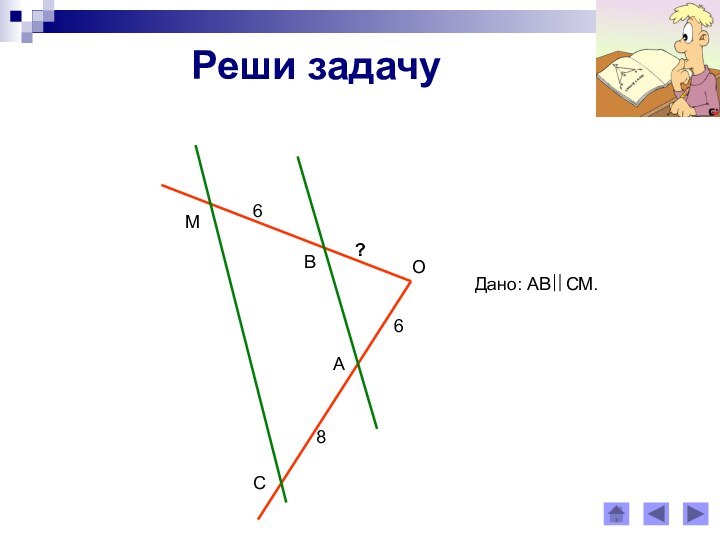

Сходственными сторонами в подобных треугольниках
называются стороны, лежащие против равных углов.
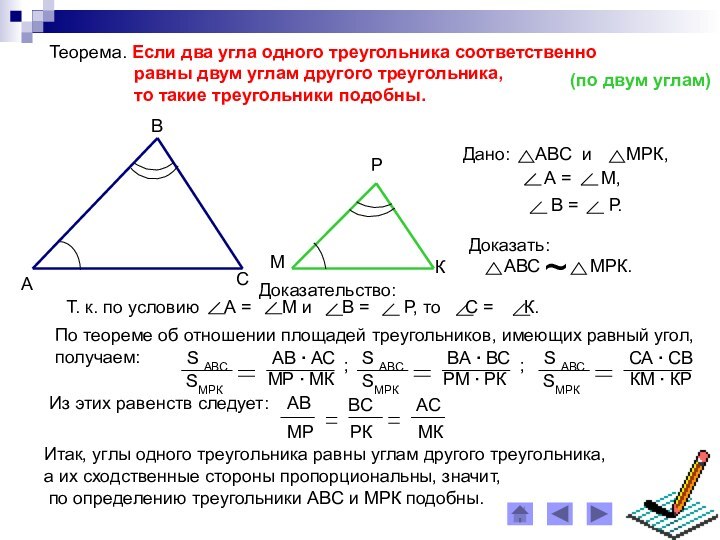
(по двум углам)
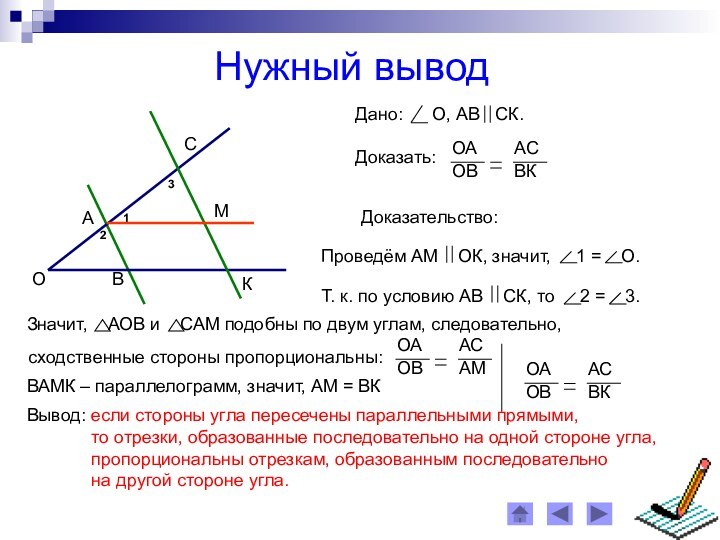
Доказательство:
По теореме об отношении площадей треугольников, имеющих равный угол,
получаем:
Итак, углы одного треугольника равны углам другого треугольника,
а их сходственные стороны пропорциональны, значит,
по определению треугольники АВС и МРК подобны.
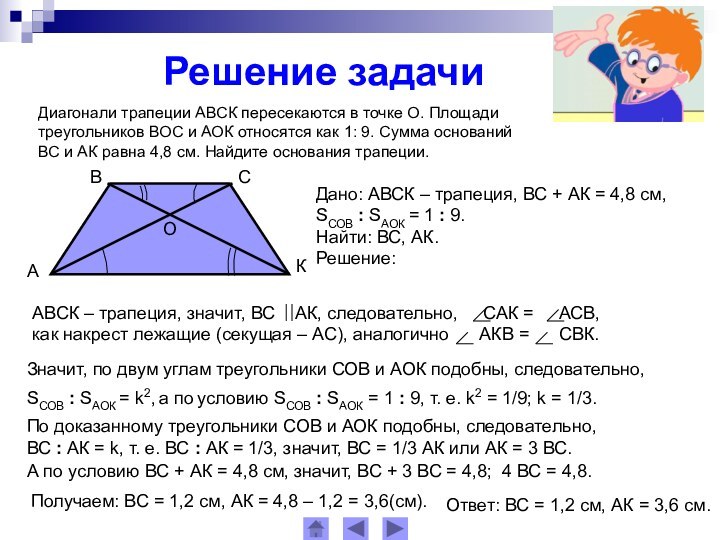
Дано: АВСК – трапеция, ВС + АК = 4,8 см,
SСОВ : SАОК = 1 : 9.
Найти: ВС, АК.
Решение:
Значит, по двум углам треугольники СОВ и АОК подобны, следовательно,
SСОВ : SАОК = k2, а по условию SСОВ : SАОК = 1 : 9, т. е. k2 = 1/9; k = 1/3.
По доказанному треугольники СОВ и АОК подобны, следовательно,
ВС : АК = k, т. е. ВС : АК = 1/3, значит, ВС = 1/3 АК или АК = 3 ВС.
А по условию ВС + АК = 4,8 см, значит, ВС + 3 ВС = 4,8; 4 ВС = 4,8.
Получаем: ВС = 1,2 см, АК = 4,8 – 1,2 = 3,6(см).
Ответ: ВС = 1,2 см, АК = 3,6 см.