Слайд 3
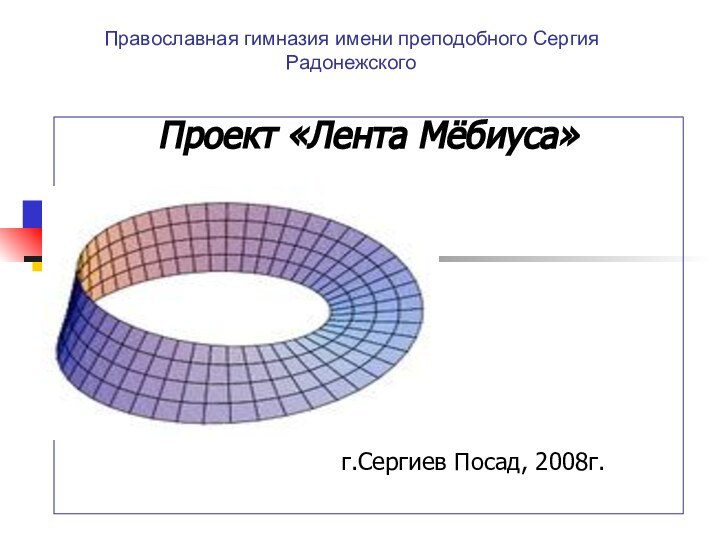
Лист Мёбиуса (другое название — Лента Мёбиуса) —простейшая
односторонняя поверхность с краем. Попасть из одной точки этой
поверхности в любую другую можно, не пересекая края. Лента Мёбиуса была обнаружена независимо немецкими математиками Августом Фердинандом Мёбиусом и Иоганном Бенедиктом Листингом в 1858г. Модель ленты Мёбиуса может легко быть сделана. Для этого надо взять достаточно вытянутую бумажную полоску и соединить концы полоски, предварительно перевернув один из них.
В евклидовом пространстве существуют два типа полос Мёбиуса в зависимости от направления закручивания: правые и левые.
Определение
Слайд 5
Свойства
Лента Мёбиуса обладает любопытными свойствами. Если попробовать разрезать
ленту пополам по линии, равноудалённой от краёв, вместо двух
лент Мёбиуса получится одна длинная двухсторонняя (вдвое больше закрученная, чем лента Мёбиуса) лента, которую фокусники называют «афганская лента». Если теперь эту ленту разрезать посередине, получаются две ленты намотанные друг на друга. Если же разрезать ленту Мёбиуса, отступая от края приблизительно на треть её ширины, то получаются две ленты, одна — более тонкая лента Мёбиуса, другая — длинная лента с двумя полуоборотами («афганская лента»). Другие интересные комбинации лент могут быть получены из лент Мёбиуса с двумя или более полуоборотами в них. Например, если разрезать ленту с тремя полуоборотами, то получится лента, завитая в узел трилистника. Разрез ленты Мёбиуса с дополнительными оборотами даёт неожиданные фигуры, названные парадромными кольцами.
Слайд 6
Бутылка Кляйна
Тесно связанным с лентой Мебиуса является загадочный

объект - бутылка Кляйна. Бутылка Кляйна может быть создана
склеиванием двух лент Мебиуса друг с другом вдоль их границ. Эта операция не может быть произведена в трехмерном пространстве без создания пересечений внутри фигуры.
Бутылка Кляйна - это математическая неориентируемая поверхность, в которой неразличимы внутренняя и внешняя стороны. Бутылка Кляйна впервые была описана в 1882 году немецким математиком Феликсом Кляйном (Felix Klein).
Представим себе бутылку с отверстием в дне. Теперь мысленно удлиним горлышко бутылки, изогнем его в обратном направлении и направим внутрь бутылки сквозь стенку, не касаясь её (это невозможно произвести в трехмерном пространстве), далее удлиним горлышко до дна бутылки и соединим края горлышка с краями отверстия в дне бутылки. Настоящая бутылка Кляйна в четырехмерном пространстве не пересекается сама с собой.
В отличие от реальных бутылок, поверхность Кляйна не имеет границы, где бы она прерывалась. В отличие от шара или тора, муха, ползущая по поверхности бутылки Кляйна, может попасть с внешней стороны на внутреннюю, не проходя сквозь поверхность.
Слайд 7
Разновидности бутылки Кляйна
Слайд 8
Искусство
Лист Мёбиуса служил вдохновением для скульптур и для
графического искусства. Морис Корнилис Эшер был одним из художников,
кто особенно любил его и посвятил несколько своих литографий этому математическому объекту. Одна из известных «Лист Мёбиуса II» показывает муравьёв, ползающих по поверхности ленты Мёбиуса.
Лист Мёбиуса также постоянно встречается в научной фантастике, например, в рассказе Артура Кларка «Стена Темноты». Иногда научно-фантастические рассказы предполагают, что наша вселенная может быть некоторым обобщенным листом Мёбиуса. Так же кольцо Мёбиуса постоянно упоминается в рассказах уральского писателя Владислава Крапивина, цикл «В глубине великого кристалла» (напр. «Застава на Якорном Поле») . В рассказе «Лист Мёбиуса» автора А. Дж. Дейча, бостонское метро строит новую линию, маршрут которой становится настолько запутанным, что превращается в ленту Мёбиуса, после чего на этой линии начинают исчезать поезда.
Слайд 9
«Кельтская лента» Пола Билацика и
«Лист Мёбиуса II» голландского
художника
Морица Корнилиса Эшера.
Слайд 10
Технология
Существовали технические применения ленты Мёбиуса. Полоса ленточного конвейера
выполнялась в виде ленты Мёбиуса, что позволяло ему работать
дольше, потому что вся поверхность ленты равномерно изнашивалась. Также в системах записи на непрерывную плёнку применялись ленты Мёбиуса (чтобы удвоить время записи). В матричных принтерах красящая лента также имела вид лист Мёбиуса для увеличения срока годности.
Устройство под названием резистор Мёбиуса — это недавно изобретённый электронный элемент, который не имеет собственной индуктивности. Никола Тесла запатентовал подобное устройство в начале 1900-х, патент US#512,340. Катушка для электромагнитов предназначалась для использования его в системе глобальной передачи электричества без проводов.
Слайд 11
Кандидат физико-математических наук Юрий Арутюнов.
Он установил две ленты

Мёбиуса на концах самолётного крыла, и сопротивление воздушной среды
снизилось. За счёт этого экономия авиационного топлива составила 7–10%. Но есть ещё один результат применения такого маленького приспособления, особенно актуальный для российской авиации: разгрузив крыло с помощью лент Мёбиуса на 20%, можно увеличить ресурс самолёта на все 100%, то есть даровать ему вторую жизнь. Особенно это ценно для такой проверенной и оправдавшей себя марки самолёта, как Ил-76. В скором времени все эти машины должны выйти из строя, а равноценной замены им нет.
В виде парадоксальной геометрической фигуры можно, оказывается, изготовить лопасти бетономешалки или обычного бытового миксера — энергозатраты снизятся на одну пятую, а качество бетона (или кондитерского крема) улучшится.
А если намотать на катушку медную проволоку не просто по кругу, но по траектории ленты Мёбиуса, индукция такого трансформатора окажется почти вдвое ниже, что и медь сэкономит, и повысит КПД. Пока приходилось эту хитрую обмотку делать вручную, но вот уже готово устройство и для машинного наматывания проволоки.
Бывает, однако, требуется решить обратную задачу — увеличить индукцию (в тех случаях, когда трансформатору приходится работать на холостом ходу). И здесь выручает намотка по закону ленты Мёбиуса, только с поворотом в другую сторону.
В трансформаторах встречаются «паразитные» токи — по имени первооткрывателя их называют токи Фуко. Они только попусту разогревают металл да могут ещё и шибануть. Вот и приходится с ними бороться. Намотка проволоки в виде ленты Мёбиуса позволяет пустить на двух катушках токи Фуко навстречу друг другу — и они гасят сами себя.
Универсальная деталь «скелета» любого цилиндрического корпуса — что для самолёта или ракеты, что для подводной лодки -кольцевой шпангоут. Он «обречён» вечно испытывать разрушительное для себя противоречие: внутренний слой шпангоута сжат, а внешний растянут. Понятно, что такие напряжения материала не способствуют его долголетию. А вот не уставший от детской игры Арутюнов взял да и скрутил шпангоут -уже догадались как? Нагрузки так перераспределились, что срок жизни конструкции удвоился.