Презентация на тему Полуправильные многоугольники

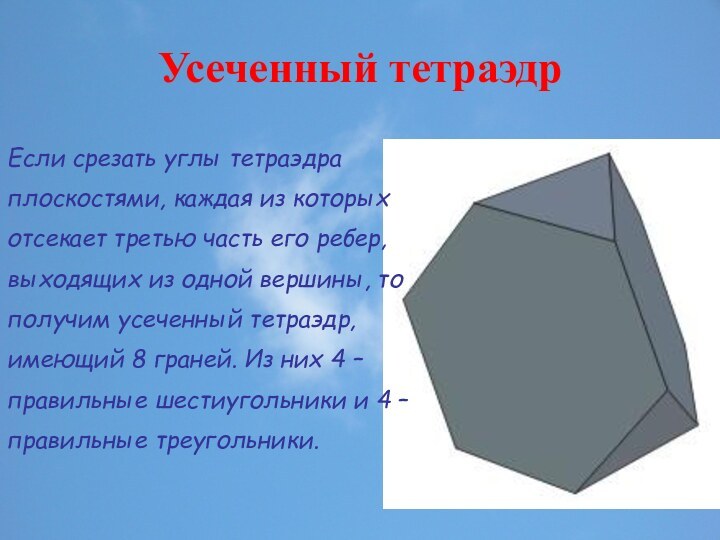
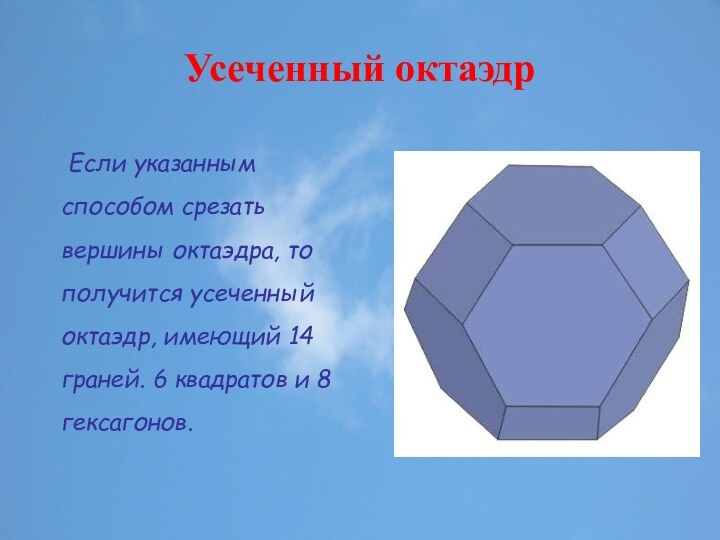
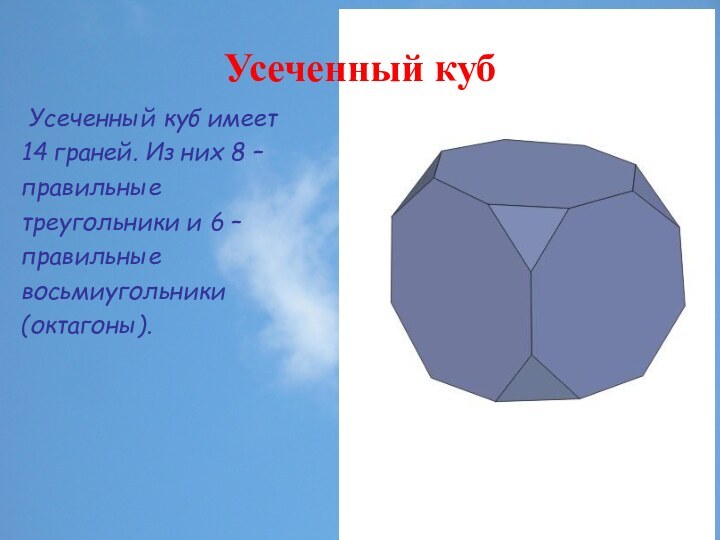
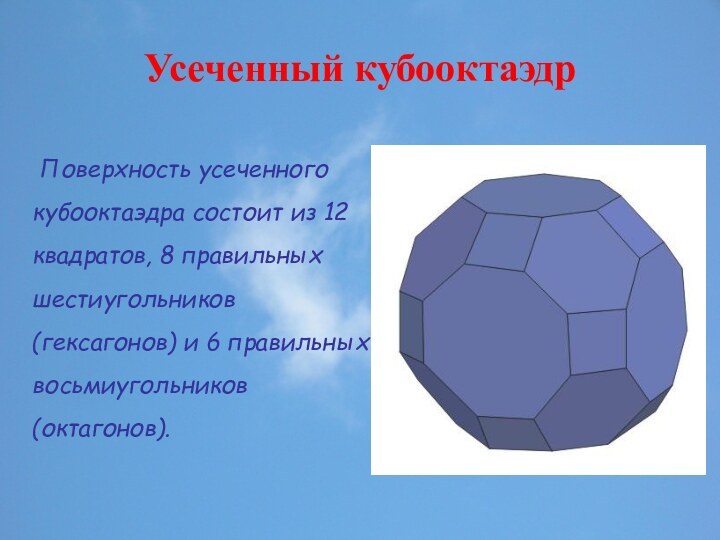
или Платоновых тел являются однотипные правильные многоугольники (треугольники, квадраты

и пентагоны), то гранями полуправильных многогранников, являются правильные многоугольники разных типов.
К полуправильным многогранникам относят n-угольные призмы, все ребра которых равны, а также антипризмы.
Кроме этих двух бесконечных серий полуправильных многогранников имеется 13 полуправильных многогранников, которые впервые открыл и описал Архимед, - это тела Архимеда.

из которых отсекает третью часть его ребер, выходящих из

одной вершины, то получим усеченный тетраэдр, имеющий 8 граней. Из них 4 – правильные шестиугольники и 4 – правильные треугольники.

то получится усеченный октаэдр, имеющий 14 граней. 6 квадратов

и 8 гексагонов.

них 8 – правильные треугольники и 6 – правильные

восьмиугольники (октагоны).

них 12 – правильные пятиугольники (пентагоны)
и 20 –

правильные шестиугольники (гексагоны). Поверхность футбольного мяча изготавливают в форме поверхности усеченного икосаэдра

них 20 – правильные треугольники и 12 -правильные десятиугольники

(декадоны).

середины ребер, выходящих из одной вершины, то получим икосододекаэдр.

У него 20 граней – правильные треугольники и 12 – правильные пятиугольники (пентагоны), то есть все грани икосаэдра и додекаэдра.

октаэдра, к которым добавлено еще 12 квадратов. Итого ромбокубооктаэдр

имеет 8 треугольников и 18 квадратов.

треугольников и 6 квадратов.

и еще 30 квадратов. Итого он имеет 62 грани.

Из них 20 треугольников, 30 квадратов и 12 пентагонов.

куба окруженных правильными треугольниками. У него 38 граней. Из

них 32 треугольника и 6 квадратов.

правильными треугольниками. 85 треугольников и 12 пентагонов.

квадратов, 8 правильных шестиугольников (гексагонов) и 6 правильных восьмиугольников

(октагонов).

квадратов, 20 правильных шестиугольников (гексагонов) и 12 правильных десятиугольников

(декагонов).

ромбокубооктаэдра поворотом его верхней восьмиугольной «крышки» на 45 градусов

по оси –
открыл Миллер в 1930 г. и независимо от него В. Г. Ашкинузе и Л. Есаулова.