Слайд 2
Результаты обучения
знать, что такое противоположные события и уметь
находить вероятность одного из них по вероятности другого;
понимать, что
такое пересечение и объединение событий, уметь изображать на диаграммах Эйлера;
понимать, что такое несовместные события;
знать и уметь применять формулу сложения вероятностей для несовместных событий; желательно знание формулы сложения для произвольных событий;
знать, что такое независимые события (и не путать их с несовместными);
уметь применять формулу умножения вероятностей независимых событий.
Слайд 3
Теоретический материал
Случайное событие или просто событие – это
некоторое множество (набор, совокупность) элементарных событий.
Событием, противоположным событию А
, называют событие, которому благоприятствуют все элементарные события, не благоприятствующие событию А. Событие, противоположное событию А, обозначают Ā. События А иĀ называют взаимно противоположными или дополнениями друг к другу.
Объединением (суммой событий) А и В называется событие, которое происходит в том и только том случае, если происходит хотя бы одно из событий А и В
(это означает либо А, либо В, либо А и В вместе).
Пересечением (произведением событий) А и В называется событие, которое происходит в том и только том случае, когда наступают оба события А и В.
Несовместными называются события, которые не могут наступить в одном и том же опыте вместе (одновременно). Их пересечение пустое множество. Вероятность объединения несовместных событий равна сумме их вероятностей Р (А В) = Р(А) + Р(В)
Слайд 4
Теоретический материал
Вероятность объединения двух любых событий
Р(А
В) = Р(А) + Р(В) – Р(А∩В)
Случайный выбор одного
предмета из группы – это выбор, при котором все предметы имеют равные шансы быть выбранными. Если в группе N предметов, то при случайном выборе каждый из них может быть выбран с вероятностью 1/N.
Два события называются независимыми, если вероятность их пересечения равна произведению их вероятностей Р(А∩В) = Р(А) Р(В). Часто независимость событий объясняется независимостью опытов , к которым они относятся.
Слайд 5
п. 32 задача 5
Бросают одну игральную кость. Событие
А состоит в том, что:
а) Выпала шестерка;
б) выпало четное
число очков;
в) выпало число очков, кратное трем.
Для каждого случая перечислите элементарные события, благоприятствующие событию ͞А, опишите событие ͞А словами и найдите Р(͞А).
Слайд 6
п.32 задача 5 решение:
а) событие А – выпала
«6» Р(А)= 1/6,
событие Ā -
выпала «1», «2», «3», «4», «5»
Р(Ā) = 5/6.
б) событие А – выпало четное число очков «2»,
«4», «6» Р(А) = 3/6 = 1/2,
событие Ā – выпало нечетное число очков «1»,
«3», «5» Р(Ā) = 3/6 = 1/2.
в) событие А – выпало число очков, кратное трем
«3», «6» Р(А) = 2/6 = 1/3,
событие Ā - выпало число очков, не кратное
трем «1», «2», «4», «5» Р(Ā) = 4/6 = 2/3.
Слайд 7
п. 32 задача 6
Бросают две игральные кости. Событие
А состоит в том, что в сумме на них
выпало:
а) два очка;
б) 12 очков;
в) менее 4 очков;
г) более 10 очков.
Для каждого случая опишите событие Ā словами и найдите Р(Ā).
Для решения задачи можно воспользоваться формулой Р(А) + Р(Ā)=1.
Слайд 8
п. 32 задача 6 решение:
а) событие А -
выпало 2 очка (1;1) Р(А) = 1/36,
событие Ā – не выпало 2 очка
Р(Ā) = 1 – 1/36 = 35/36.
б) событие А - в сумме выпало 12 очков (6; 6)
Р(А) = 1/36,
событие Ā – в сумме не выпало 12 очков
Р(Ā) = 1 -1/36 = 35/36.
Слайд 9
п.32 задача 6 решение:
в) событие А - в
сумме выпало менее 4 очков
(1;
1), (1; 2), (2; 1) Р(А) = 3/36 = 1/12,
событие Ā – в сумме выпало более 4 очков
Р(Ā) = 1 -1/12 = 11/12.
г) событие А – в сумме выпало более 10 очков
(5; 6), (6; 5), (6; 6) Р(А) = 3/36 = 1/12,
событие Ā – в сумме выпало менее 10 очков
Р(Ā) = 1 – 1/12 = 11/12.
Слайд 10
п. 32 задача 8
Симметричную монету бросили 4 раза.
Орел при этом может выпасть 1, 2, 3 и
4 раза, а может не выпасть ни разу. Вероятности этих событий представлены в таблице:
Слайд 11
п. 32 задача 8
Найдите вероятность события, противоположного событию:
а)
«орел не выпал ни разу»;
б) « орел выпал более
одного раза»;
в) «решка выпала менее трех раз»;
г) «орел выпал неизвестно сколько раз, но точно не два раза».
Слайд 12
п.32 задача 8 решение:
а) событие А – «орел
не выпал ни разу»
Р(А)
= 1/16, Р(Ā) = 1 -1/16 = 15/16.
б) событие А - «орел выпал более одного раза»
Р(А) = 3/8 + 1/4 + 1/16 = 11/16,
Р(Ā) = 1 – 11/16 = 5/16.
в) событие А – « решка выпала менее трех раз»
Р(А) = 1/16 + 1/4 + 3/8 = 11/16
Р(Ā) = 1 -11/16 = 5/16.
г) событие А – «орел выпал неизвестно сколько
раз, но точно не два»
Р(А) = 1/16 + 1/4 + 1/4 + 1/16 = 10/16 = 5/8,
Р(Ā) = 1 – 5/8 = 3/8.
Слайд 13
П.32 задача 9
Из класса выбирают двух учеников.
Опишите словами событие, противоположное событию В , если событие
В состоит в том, что:
а) оба выбранных ученика — мальчики;
б) выбраны ученики одного пола.
Слайд 14
п.32 задача 9 решение:
Из класса выбирают двух
учеников. Элементарные события: ММ, ДД, МД, ДМ.
а) Событие В
– «оба выбранных ученика мальчики» ММ.
Событием, противоположным событию В, называют событие, которому благоприятствуют все элементарные события, не благоприятствующие событию В. (Обозначают ͞В)
Событие ͞В : ДД, МД, ДМ «хотя бы одна девочка»
б) Событие В – «выбраны ученики одного пола» ММ, ДД.
Событие ͞В : МД, ДМ «выбраны ученики разного пола»
Слайд 15
п.33 задача 3
Событию А благоприятствует 6 элементарных событий,
а событию В 8 элементарных событий. Из этих 8
элементарных событий 4 благоприятствует сразу 2 событиям. Нарисуйте диаграмму Эйлера и ответьте на вопросы.
а) Сколько элементарных событий благоприятствует событию А, но не благоприятствует событию В?
б) Сколько элементарных событий благоприятствует событию В, но не благоприятствует событию А?
в) Сколько элементарных событий благоприятствует событию А В?
Слайд 16
п.33 задача 3 решение:
а) 2 события благоприятствуют А,
но не благоприятствуют В.
б) 4 события благоприятствуют В, но
не благоприятствуют А.
в) 10 событий благоприятствуют событию
А В.
4
4
2
Слайд 17
п. 33 задача 4
Монету бросают дважды. Событие
А – «первый раз выпал орел». Событие В –
«второй раз выпал орел» Выпишите элементарные события, благоприятствующие каждому из этих событий и событию А В.
Слайд 18
п. 33 задача 4 решение:
Элементарные события опыта: ОР,
ОО, РО,РР.
Событию А благоприятствуют элементарные события: ОР, ОО.
Событию В
благоприятствуют элементарные события: ОО; РО.
Событию А В благоприятствуют элементарные события: ОР; ОО; РО.
Слайд 19
п.33 задача 6
На диаграмме Эйлера изображены события А
и В.Нарисуйте диаграмму в тетради и укажите на ней
событие С, которое состоит в том, что:
а) событие А наступило, а В - нет ;
б) событие В наступило, а А – нет;
в) наступило хотя бы одно из событий А и В;
г) не наступило ни одно из событий А и В;
д) наступили оба события.
Какое из событий пунктов а) –д) является событием А В? Какое из событий пунктов а) – д)является событием ͞͞А͞ ͞В?
Слайд 21
п.33 задача 7
Бросают одну игральную кость. Событие А
«выпало четное число очков». Событие В состоит в том,
то:
а) выпало число очков, кратное 3;
б) выпало нечетное число очков;
в) выпало число очков, кратное 4;
г) выпало число очков, кратное 5;
Выпишите все элементарные события, благоприятствующие событию А В. Найдите Р(А В).
Слайд 22
п.33 задача 7 решение:
Элементарным событием опыта можно считать
выпадение чисел: 1, 2, 3, 4, 5, 6.
а) событию
А благоприятствуют элементарные события: 2, 4, 6. Событию В благоприятствуют элементарные события: 3, 6.
Событию А В: 2, 3, 4, 6 (выпало либо четное, либо кратное трем число очков).
Р(А В) = N (A B)/N, где N(A B)= 4, N = 6.
Р(А В) = 4/6 = 2/3.
Ответ: 2/3
Слайд 23
п.33 задача 7 решение:
б) Событию В благоприятствуют элементарные
события : 1, 3, 5.
Событию А В :
1, 2, 3, 4, 5, 6 ( выпало либо четное число очков, либо нечетное число очков).
N(А В) = 6, Р(А В) = 6/6 = 1.
Ответ: 1
в) Событию В благоприятствует элементарное событие: 4 (выпало число очков, кратное 4).
Событию А В: 2, 4, 6.
N(А В) = 3, Р(А В) = 3/6 = 1/2.
Ответ: 1/2.
Слайд 24
п.33 задача 7 решение:
г) Событию В благоприятствует
элементарное событие: 5 (выпало число очков, кратное 5).
Событию А В: 2, 4, 5, 6 (выпало четное число очков, либо число очков, кратное 5).
N(А В) = 4 Р(А В) = 4/6 = 2/3.
Ответ: 2/3
Слайд 25
п.33 задача 9
Бросают две игральные кости. Событие А
– « на первой кости выпала 1». Событие В
– « на второй кости выпала 1».
а) Выпишите все элементарные события, благоприятствующие событию А В.
б) Есть ли у событий А и В общие благоприятствующие события? Если да, то сколько их?
в) Опишите словами событие А В.
г) Найдите вероятность события А В.
Слайд 26
п.33 задача 9 решение:
а) Событие А U В:
(1;1), (1;2), (1;3), (1;4), (1;5), (1;6), (2;1), (3;1), (4;1),
(5;1),( 6;1).
N(А В)= 11.
б) 1 событие.
в) «хотя бы на одной кости выпала 1».
г) Р(А В) = N(А В)/N
Р(А В) = 11/36.
Слайд 27
п.34 задача 1
Бросают одну игральную кость. Событие
А -
«выпало четное число очков». Событие
В заключается в том, что:
а) выпало число, кратное 3;
б) выпало число очков, кратное 4;
г) выпало число очков, большее 4;
д) выпало число очков меньшее 3.
Для каждого случая выпишите элементарные события, составляющие событие А В, и найдите Р(А В).
Слайд 28
п. 34 задача 1 решение:
Элементарные события: 1, 2,
3, 4, 5, 6.
Событию А благоприятствуют элементарные события:
2, 4, 6 (выпало четное число очков).
а) Событию В благоприятствуют: 3, 6 (выпало число очков, кратное 3).
Событию А В благоприятствуют: 6.
N(А В) = 1 Р(А В) = 1/6.
б) Событие В: 4 (выпало число очков, кратное 4).
Событию А В: 4.
Р(А В) = 1/6.
в) и г) выполняются аналогично: в) 1/6; г)1/6.
Слайд 29
п.34 задача 3
Из класса случайным образом выбирают двух
учеников. Событие D – «первый выбранный ученик –девочка». Событие
С – « второй выбранный ученик – девочка». Опишите словами события D С, D С.
Слайд 30
п. 34 задача 3 решение:
Элементарные события опыта: ДМ,
МД, ДД,ММ.
Элементарные события благоприятствующие событию D: ДМ, ДД.
Элементарные события,
благоприятствующие событию С: ДД, МД.
а) D C: ДМ, МД, ДД (хотя бы один ученик – девочка).
б) D C: ДД ( оба ученика – девочки)
Слайд 31
п.34 задача 6
Событие С – «по дороге из
школы домой вам встретится черная кошка».
Событие D –
«по дороге домой вам встретится злая собака.
Опишите словами объединение и пересечение этих событий.
Слайд 32
п.34 задача 6 решение:
Пересечение событий C и D
происходит, если мы встречаем и кошку и собаку.
Объединение событий
C и D происходит, если мы встречаем либо кошку, либо собаку, либо кошку и собаку вместе.
Слайд 33
п.34 задача 7
Событие М –
«вас завтра вызовут к доске на уроке математики».
Событие G – «вас завтра вызовут к доске на уроке географии».
Опишите словами объединение и пересечение этих событий.
Слайд 34
п. 34 задача 7 решение:
M G -
вас завтра вызовут к доске хотя бы на одном
из 2-х уроков.
M G - вас завтра вызовут к доске на двух уроках .
задача 8
В ходе некоторого опыта событию А благоприятствуют 6
элементарных событий, событию В – 8 элементарных событий. При этом 2 элементарных события благоприятствуют событию А ⋂ В. Сколько элементарных событий благоприятствует событию:
а) «событие А наступает, а В – нет»;
б) «событие В наступает, а А – нет».
Нарисуйте диаграмму Эйлера, на которой в каждой из образовавшихся фигур укажите число элементарных событий, благоприятствующих соответствующему событию.
Пользуясь рисунком, ответьте на вопрос: сколько элементарных событий благоприятствует событию
А ⋃ В?
Слайд 36
п. 34 задача 8 решение:
6 элементарных событий, благоприятствующих для опыта А.
8 элементарных
событий, благоприятствующих для опыта В.
2 элементарных события благоприятствуют событию А ⋂ В
6
8
6=4+2
8=2+6
4
2
6
6
8
Слайд 37
п.34 задача 8 решение:
а)«событие А наступает, а В
– нет».
6 – 2= 4
Потому что 2 элементарных
события благоприятствует событию А ⋂ В, а значит не могут благоприятствовать этому событию.
4
2
6
6
8
Слайд 38
п. 34 задача 8 решение:
б) «событие В наступает,
а А – нет».
8 – 2 = 6
Потому
что 2 элементарных события благоприятствуют событию А ⋂ В, а значит не могут благоприятствовать этому событию.
4
2
6
6
8
Слайд 39
п. 36 задача 5
Вероятность того, что по дороге
из школы домой вы встретите черную кошку, равна 0,1.
Вероятность того, что по дороге из школы домой вы встретите злую собаку, равна 0,4. Вероятность того, что вам встретится и черная кошка и злая собака равна 0,04.
а) Найдите вероятность того, что вам встретится хотя бы одно из этих животных;
б) Найдите вероятность того, что вы не встретите ни черную кошку, ни злую собаку.
Слайд 40
п. 36 задача 5 решение:
а) Найдите вероятность того,
что вам встретится хотя бы одно из этих животных;
Р(А В) = Р(А) + Р(В) – Р(А В)
Р(С) = Р(А В) = 0,1 + 0,4 – 0,04 = 0,46.
б) Найдите вероятность того, что вы не встретите ни черную кошку, ни злую собаку;
Рассмотрим противоположное событие и найдем его вероятность
Р( )= 1 -Р(А В) = 1 – 0,46 = 0,56
Слайд 41
п.36 задача 6
Вероятность того, что вас вызовут завтра
к доске на первом уроке, равна 0,1. Вероятность того,
что вас вызовут завтра к доске на втором уроке равна 0,3. Вероятность того, что вас вызовут завтра и на первом и на втором уроках, равна 0,03. Найдите вероятность того, что вас завтра:
а) вызовут хотя бы на одном из двух первых уроков;
б) не вызовут ни на одном из двух первых уроков.
Слайд 42
п. 36 задача 6 решение:
а) Найдите вероятность того,
что вас завтра вызовут хотя бы на одном из
двух первых уроков;
Р(А В) = Р(А) + Р(В) – Р(А В)
Р(С) = Р(А В) = 0,1 + 0,3 – 0,03 = 0,37.
б) Найдите вероятность того, что вас завтра не вызовут к доске ни на одном из двух первых уроков;
Р( )= 1 - Р(А В) = 1 – 0,46 = 0,56
Слайд 43
п. 36 задача 7*
Пользуясь диаграммой Эйлера для событий
А, В и С, докажите формулу сложения вероятностей для
трех событий.
Р(А В С) = Р(А) + Р(В) + Р(С) – Р(А В) – Р(А С) + Р(А В С)
Слайд 45
п.36 задача 7 решение:
Рассмотрим события:
D – «наступило
А, но В и С не наступило»
E – «наступило
В, но А и С не наступило»
F - «наступило С, но А и В не наступило»
К – «наступило А и В, но С не наступило»
L – «наступило В и С, но А не наступило»
М – «наступило А и С, но В не наступило»
Все события, изображенные на диаграмме D, К, М и А В С несовместны, так как соответствующие фигуры не имеют общих точек. Вместе они образуют событие А. Поэтому по правилу сложения вероятностей для несовместных событий
Р(А) = Р(D) + Р(К) + Р(М) + Р(А В С).
Аналогично Р(В) = Р(Е) + Р(К) + Р(L) + Р (А В С)
Р(С) = Р(F) + Р(L) + Р(М) + Р (А В С)
Слайд 46
п.36 задача 7 решение:
Р(А) + Р(В)+ Р(С)
= Р(D)+ Р(Е) + Р(К) + Р(L) + P(M)
+ P(A B C) + P(K) + P(L) + P(M) +
+ P(A B C) + P(A B C)
Р(А) + Р(В) + Р(С) = Р(А В С) + Р(А В)+
+ Р(В С) + Р(М)
Р(А В С) = Р(А) + Р(В) + Р(С) – Р(А В)
–Р(В С) – Р(М)
Р(М) + Р(А В С) = Р(А С) Р(М) = Р(А С) - Р(А В С)
Р(А В С) = Р(А) + Р(В) + Р(С) – Р(А В) – Р(А С) + Р(А В С)
Слайд 47
п. 38 задача 8
Монету бросили два раза. Событие
А – «первый раз выпал орел». Событие В –
«второй раз выпала решка».
а) Выпишите все элементарные события этого случайного эксперимента.
б) Сколько элементарных событий благоприятствует событию А, и сколько событию В?
в) Найдите вероятности событий А, В и А В.
г) Являются ли события А и В независимыми?
Слайд 48
п.38 задача 8 решение:
а)Выпишите все элементарные события этого
случайного эксперимента.
ОО, РР, ОР, РО.
б)Сколько элементарных событий
благоприятствует событию А, и сколько событию В?
событие А (первый раз выпал орел) ОО, ОР – 2 элементарных события,
событие В (второй раз выпала решка) РР, ОР – 2 элементарных события.
в) Найдите вероятности событий А, В и А В.
Р(А) = 1/2, Р(В) = 1/2, Р(А В) = 1/2 1/2 = 1/4,
события благоприятствующие А В - ОР ( 1 событие)
Р(А В) = 1/4.
г) События А и В являются независимыми.
Слайд 49
п. 38 задача 9
Игральную кость бросают два раза.
В таблице элементарных событий этого случайного эксперимента выделите элементарные
события, благоприятствующие каждому из событий А, В и А В. Проверьте, являются ли события А и В независимыми, если:
а) А – « на первой кости четное число очков», В – « на второй кости четное число очков»;
б) А – « на первой кости нечетное число очков»,
В – « на второй кости выпало 6».
Слайд 50
п. 38 задача 9 решение:
а) А – «на
первой кости четное число очков»,
В
– « на второй кости четное число очков»
Слайд 51
п. 38 задача 9 решение:
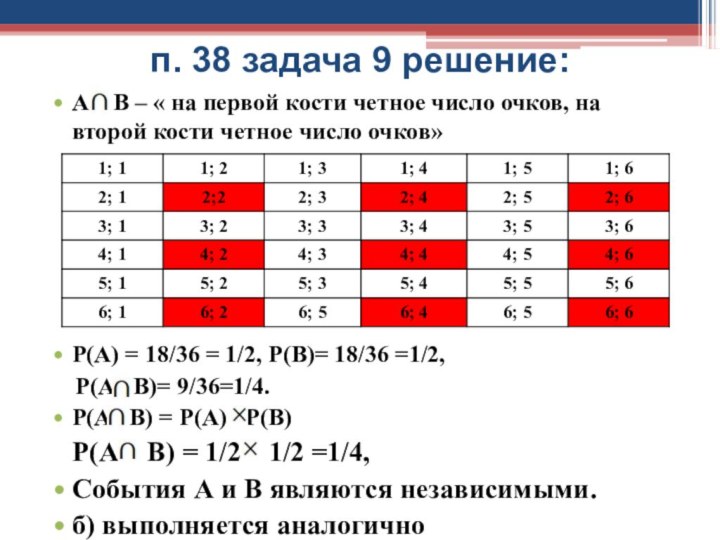
А В –
« на первой кости четное число очков, на второй
кости четное число очков»
Р(А) = 18/36 = 1/2, Р(В)= 18/36 =1/2,
Р(А В)= 9/36=1/4.
Р(А В) = Р(А) Р(В)
Р(А В) = 1/2 1/2 =1/4,
События А и В являются независимыми.
б) выполняется аналогично
Слайд 52
п.38 задача 10
Предположим, что вероятность встретить по дороге
из школы черную кошку равна 0,1, а вероятность встретить
злую собаку равна 0,3. Считая, что собака и кошка гуляют независимо друг от друга, найдите вероятность того, что по дороге из школы повстречаются и черная кошка и злая собака.
Слайд 53
Событие А – «встреча с черной кошкой»
Р(А) =0,1
Событие В – «встреча со злой собакой»
Р(В) = 0,3
Событие А и В – независимые события
Событие А В – «повстречаются и черная кошка, и злая собака»
Р(А В) = 0,1 0,3 = 0,03
п. 38 задача 10 решение:
Слайд 54
п. 38 задача 11
Вероятность того, что лампочка в
люстре перегорит в течении года, равна 0,2. Считая, что
лампочки перегорают независимо друг от друга, найдите вероятность того, что в течение года перегорят все лампочки в люстре, если в люстре:
а) две лампочки;
б) три лампочки;
в) пять лампочек.
Слайд 55
п.38 задача 11 решение:
Событие А – «лампочка в
люстре перегорит в течение года» Р(А) = 0,2
а) в
люстре две лампочки;
Р(В) = Р(А) Р(А)
Р(В) = 0,2 0,2=0,04;
б) в люстре три лампочки;
Р(В)= 0,2 0,2 0,2 = 0,008;
в) в люстре пять лампочек;
Р(В) = 0,2 0,2 0,2 0,2 0,2 = 0,00032
Слайд 56
п. 38 задача 13
Из ящика, где хранятся 9
желтых и 15 зеленых карандашей, продавец, не глядя вынимает
один за другим 2 карандаша. Найдите вероятность того, что оба карандаша окажутся:
а) желтыми;
б) зелеными.
Слайд 57
п.38 задача 13 решение:
Всего в ящике 9 +
15 = 24 карандаша.
а) оба карандаша останутся желтыми
Р(А) = 9/24 8/23 = 0,13;
б) оба карандаша окажутся зелеными
Р(А) = 15/24 14/23 =0,38.
Примечание: Всего в ящике 24 желтых карандаша, т.е. N= 24. Сколько событий благоприятствует событию «вытащить желтый карандаш» ? N(A) = 9. Вычислим по формуле Р(А) = 9/24.
В коробке после того как вытащили желтый карандаш, осталось 23 карандаша, желтых карандашей 8, следовательно N = 23, N(A) = 8. Р(А) = 8/23.
Слайд 58
п.38 задача 14
Красная Шапочка несет пирожки от мамы
к бабушке через темный лес. На рисунке изображена схема
дорожек в лесу. На каждой развилке Красная Шапочка выбирает наудачу одну из дорожек и идет по ней дальше. К дому бабушки ведет только один путь. Остальные приводят в болото или к Волку. Найдите вероятность того что Красная Шапочка благополучно дойдет до бабушки.
Слайд 59
п.38 задача 14 решение:
Р=1
р=1/3
Р=1/3
Р=1/3
Р=1/4
Р=1
р= 1/4
Р=1/4
р=1/4
Р(добраться до дома бабушки) = 2/4 =1/2
Слайд 60
п. 38 задача 14 решение:
а) Р(А) = 1/3
1/3 1/2 1/3 = 1/54;
б) Р(А)
= 1/3 1/2 1/3 2/4 =1/36.
Слайд 61
п.38 задача 15
У Ивана Ивановича есть компьютер, на
котором он пишет книгу воспоминаний. Все клавиши на клавиатуре
работают хорошо, и только клавиша М работает неправильно. С вероятностью 1/3 при нажатии этой клавиши получается буква П, а с вероятностью 2/3 – буква М. Найдите вероятность того, что фраза « Много лет назад, когда я был маленьким мальчиком» будет написана правильно с первой попытки.
Слайд 62
п.38 задача 15 решение:
«Много лет назад,
когда я был маленьким мальчиком» – 5 букв М
Событие А – «фраза будет написана правильно с первой попытки»
Р(А) = 2/3 2/3 2/3 2/3 2/3 = 0,132
Слайд 63
п. 38 задача 17*
В классе 20 человек, из
них 12 девочек. С помощью жребия из класса выбирают
4 дежурных. Найдите вероятность того, что все выбранные окажутся:
а) девочками;
б) мальчиками.
Слайд 64
п. 38 задача 17* решение:
а) Все четверо дежурных
девочки
Р(А) = 12/20 11/19 10/18
9/17 = 0,102;
б)Все четверо дежурных мальчики
Р(А) = 8/20 7/19 6/18 5/17 = 0,0144
Слайд 65
п. 38 задача 18*
На кассе продаются леденцы. В
какой-то момент в коробке осталось 10 красных, 9 синих
и 6 зеленых леденцов. Таня, Ваня и Маня по очереди покупают по одному леденцу. Кассир, не глядя, достает леденцы из коробки. Найдите вероятность того, что:
а) Таня и Ваня получат зеленые, а Маня – красный леденец;
б) Таня и Маня получат синие, а Ваня – красный;
в) Таня получит зеленый, Ваня – красный, а Маня – синий;
г) все трое получат разные леденцы.
Слайд 66
п. 38 задача 18* решение:
Всего 10 + 9
+6 =25 леденцов;
а) Таня и Ваня получат зеленые, а
Маня – красный леденец
Р(А)= 6/25 5/24 10/23 = 0,0217;
б) Таня и Маня получат синие, а Ваня – красный
Р(А) = 9/25 8/24 10/23 = 0,052;
в) Таня получит зеленый, Ваня – красный, а Маня – синий Р(А) = 6/25 10/24 9/23 = 0,039;
г) все трое получат красные леденцы
Р(А) = 10/25 9/24 7/23 = 0, 052.
Слайд 67
п. 38 задача 20*
В кармане у Нади лежит
5 леденцов и 6 ирисок. Каждую минуту Надя вынимает
наудачу сласти из кармана и отправляет их в рот. Найдите вероятность того, что через 4 минуты в кармане останется:
а) 5 леденцов и 2 ириски;
б) только 1 леденец и 6 ирисок.
Слайд 68
п.38 задача 20* решение:
Всего в кармане 5 +
6 = 11 конфет;
а) в кармане останется 5 леденцов
и 2 ириски
( из кармана Надя достанет 4 ириски)
Р(А) = 6/11 5/10 4/9 3/8 = 1/22;
б) в кармане останется только 1 леденец и 6 ирисок (из кармана Надя достанет 4 леденца)
Р(А) = 5/11 4/10 3/9 2/8 = 1/66.
Слайд 69
п.38 задача 21*
Иван Иванович звонит старому другу. Он
хорошо помнит начало номера 981 и последние четыре цифры:
3, 4, 8, 0. К сожалению, Иван Иванович забыл порядок последних четырех цифр. Найдите вероятность того, что набрав наудачу 981-30-84, он дозвониться старому другу.
Слайд 70
п. 38 задача 21* решение:
Надо набрать наудачу последние
четыре цифры
3, 4, 8, 0.
Р(А)
= 1/4 1/3 1/2 =1/24
Слайд 71
п. 38 задача 22*
В Союзе Рыжих состоит
20 членов, 12 из них математиков, остальные – литераторы.
Однажды, гуляя по городу, математик, состоящий в Союзе Рыжих, встретил по очереди двух других членов Союза. Найдите вероятность того, что:
а) первый встреченный был также математиком, а второй – литератором;
б) оба встреченных были математиками;
в) оба встреченных были литераторами;
г) первый встреченный был литератором, второй – математиком.
Слайд 72
п. 38 задача 22* решение:
Всего 20 членов: 12
математиков, 8 литераторов,
(один математик встречает по очереди
двух других членов Союза)
а) первый встреченный был также математиком, второй – литератором
Р(А) = 11/19 8/18 0,257;
б) оба встреченных были математиками
Р(А) = 11/19 10/18 0,322;
в) оба встреченных были литераторами
Р(А) = 8/18 7/19 0,164;
г) первый встреченный был литератором, второй –математиком
Р(А) =8/19 11/18 0,257.
Слайд 73
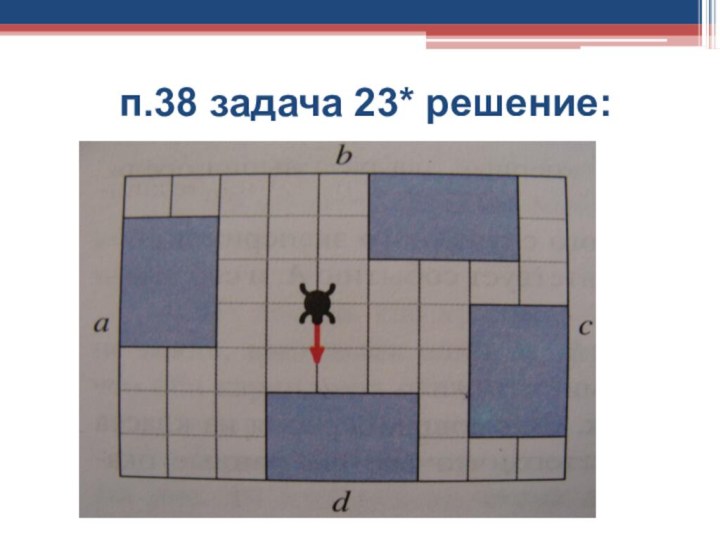
п.38 задача 23*
В комнате расположены четыре шкафа,
как показано на рисунке. Черепаха начинает ползти по направлению,
указанному стрелкой. Каждый раз натыкаясь на шкаф, черепаха поворачивает влево или вправо (с равными вероятностями) и снова ползет по прямой. Так повторяется до тех пор, пока черепаха не достигнет какой-нибудь стены комнаты. Найдите вероятность того, что черепаха остановится :
а) у стены a;
б) у стены b;
в) у стены с;
г) у стены d.
Слайд 76
п.38 задача 23* решение:
а) у стены с
Р(А) = 1/2;
б)у стены b
Р(А) =1/2
1/2 1/ 2 1/2 = 1/16;
в) у стены с
Р(А) = 1/2 1/2 1/ 2 = 1/8;
г) у стены d ( 2 пути)
Р(А) = 1/2 1/2 1/ 2 1/2 +
+ 1/2 1/2 = 1/16 + 1/4 = 5/16;
Слайд 77
п.38 задача 24*
Класс, в котором учится Миша
, состоит из 20 человек. 1 марта учитель математики
и учитель русского языка, не договариваясь между собой, случайным образом вызывают по одному ученику к доске. Вычислите вероятность того, что 1 марта:
а) Мишу вызовут к доске и на уроке математики и на уроке русского языка;
б) Мишу не вызовут к доске ни на одном из этих уроков;
в) Мишу вызовут к доске хотя бы на одном из этих уроков.
Слайд 78
п. 38 задача 24* решение:
Событие А – «Мишу
вызвали к доске на уроке математики»
Событие В – «Мишу
вызвали на уроке русского языка»
Р(А) = 1/20, Р(В) = 1/20
А и В – события независимы
Слайд 79
п. 38 задача 24* решение:
а) Мишу вызовут
к доске и на уроке математики , и на
уроке русского языка (пересечение событий)
Р(А В) = 1/20×1/20 =1/400 = 0,0025;
б) Мишу не вызовут к доске ни на одном из этих уроков (противоположное событие)
Р(Ā) = 1- Р(А); Р(Ā) = 1-1/20 = 19/20;
аналогично получаем Р(͞В) = 19/20;
Р(Ā ͞В) = Р(Ā). Р(͞В);
Р(Ā ͞В) = 19/20 . 19/20 = 361/400 = 0, 9025;
в) Мишу вызовут к доске хотя бы на одном из этих уроков (объединение событий)
Р(А В) = Р(А) + Р(В) – Р(А В)
Р(А В) = 1/20 + 1/20 - 1/400 = 39/400 = 0,0975.
Слайд 80
п.38 задача 25*
В некотором случайном
эксперименте вероятность события А равна 0,4 вероятность события В
равна 0,5. Известно, что события А и В независимые . Найдите вероятность события А В.