Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Презентация на тему Понятие центральной симметрии

Содержание

2. Содержание:ОпределениеДоказательство Применение в жизниПрименение в природеРешение задачи
3. Центральная симметрияПреобразование, переводящее каждую точку А фигуры
4. Центральная симметрияТочки М и М1 называются симметричными
5. Фигура называется симметричной относительно центра симметрии, если
6. Однако можно заметить, что центральная симметрия является
7. В курсе планиметрии мы знакомились
8. Допустим, что каждой точке М
9. Движение пространства- это отображение пространства на себя, сохраняющее расстояние между точками.AMM1
10. Центральная симметрия является движением,
11. Доказанное свойство является характерным свойством
12. Задача:Докажите,
13. Заключение Симметрию можно обнаружить почти везде, если знать,
19. Скачать презентацию
20. Похожие презентации

Содержание:ОпределениеДоказательство Применение в жизниПрименение в природеРешение задачи

Главная
Математика
Понятие центральной симметрии

Движения. Центральная симметрияВыполнила ученица 11 класса Гейнрих Юлия Проверила учительница математики Яковенко Елена Алексеевна

Содержание:ОпределениеДоказательство Применение в жизниПрименение в природеРешение задачи

Центральная симметрияПреобразование, переводящее каждую точку А фигуры в точку А1 , симметричную

Центральная симметрияТочки М и М1 называются симметричными относительно точки А, если A

Фигура называется симметричной относительно центра симметрии, если для каждой точки фигуры симметричная

Однако можно заметить, что центральная симметрия является частным случаем поворота, а именно,

В курсе планиметрии мы знакомились с движениями плоскости , т.е.

Допустим, что каждой точке М пространства поставлена в соответствие некоторая

Движение пространства- это отображение пространства на себя, сохраняющее расстояние между точками.AMM1

Центральная симметрия является движением, изменяющим направления на противоположные. То

Доказанное свойство является характерным свойством центральной симметрии, а именно, справедливо

Задача:Докажите, что при центральной симметрии:а)прямая, не

Заключение Симметрию можно обнаружить почти везде, если знать, как ее искать. Многие народы

Слайды презентации

Слайд 2 Содержание:
Определение
Доказательство
Применение в жизни
Применение в природе
Решение задачи

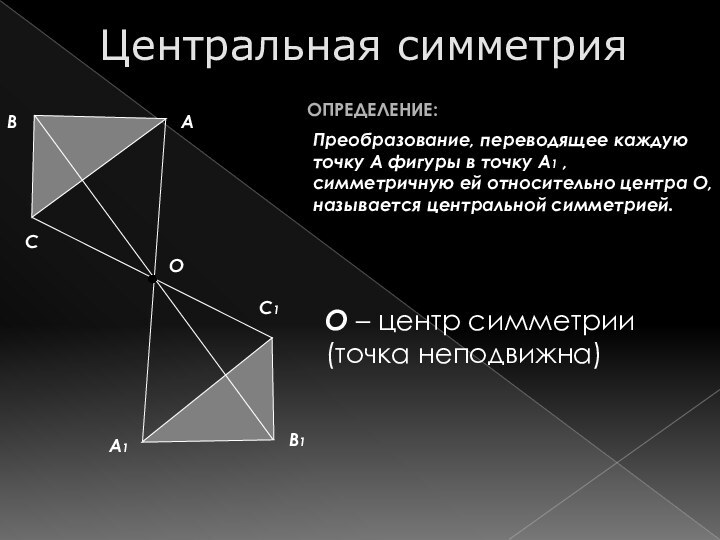
Слайд 3 Центральная симметрия
Преобразование, переводящее каждую точку А фигуры в

Центральная симметрияПреобразование, переводящее каждую точку А фигуры в точку А1 ,

точку А1 , симметричную ей относительно центра О, называется

центральной симметрией.

ОПРЕДЕЛЕНИЕ:

О – центр симметрии (точка неподвижна)

А1

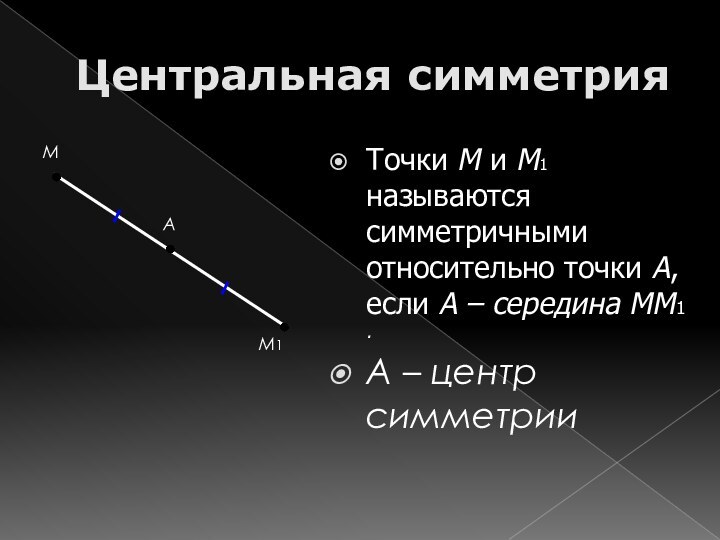
Слайд 4 Центральная симметрия
Точки М и М1 называются симметричными относительно

Центральная симметрияТочки М и М1 называются симметричными относительно точки А, если

точки А, если A – середина MM1 .
A –

центр симметрии

Слайд 5 Фигура называется симметричной относительно центра симметрии, если для

Фигура называется симметричной относительно центра симметрии, если для каждой точки фигуры

каждой точки фигуры симметричная ей точка также принадлежит этой

фигуре.

Слайд 6 Однако можно заметить, что центральная симметрия является частным

Однако можно заметить, что центральная симметрия является частным случаем поворота, а

случаем поворота, а именно, поворота на 180 градусов. Действительно,

пусть при центральной симметрии относительно точки O точка X перешла в X'. Тогда угол XOX'=180 градусов, как развернутый, и XO=OX', следовательно, такое преобразование является поворотом на 180 градусов. Отсюда также следует, что центральная симметрия является движением.

Слайд 7 В курсе планиметрии мы знакомились с

движениями плоскости , т.е. отображениями плоскости на себя, сохраняющими

расстояния между точками. Введем теперь понятие движения пространства. Предварительно разъясним, что понимается под словами отображение пространства на себя.

Слайд 8 Допустим, что каждой точке М пространства

поставлена в соответствие некоторая точка М1, причем любая точка

М1 пространства оказалась поставленной в соответствие какой-то точке М. Тогда говорят, что задано отображение пространства на себя.

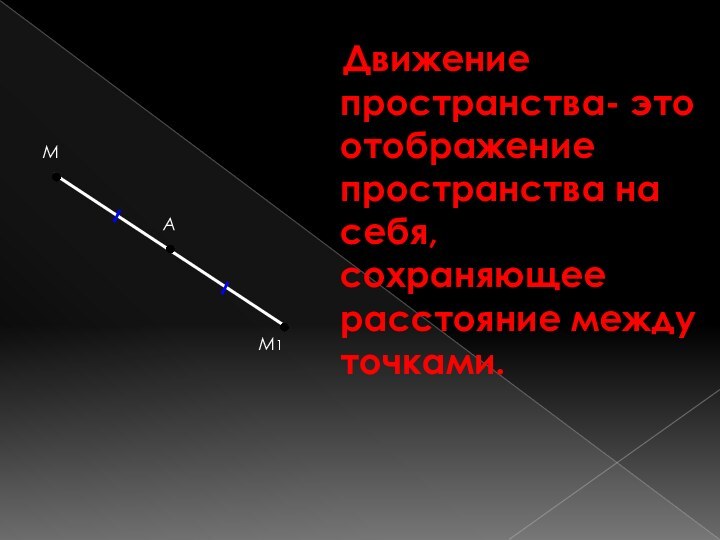
Слайд 9 Движение пространства- это отображение пространства на

себя, сохраняющее расстояние между точками.
A
M
M1

Слайд 10 Центральная симметрия является движением, изменяющим

направления на противоположные. То есть если при центральной симметрии

относительно точки O точкам X и Y соответствуют точки X' и Y', то
XY= - X'Y'
Доказательство:
Поскольку точка O - середина отрезка XX', то, очевидно,
OX'= - OX
Аналогично
OY'= - OY
Учитывая это, находим вектор X'Y':
X'Y'=OY'OX'=OY+OX=(OYOX)= XY
Таким образом, X'Y'=XY.

Слайд 11 Доказанное свойство является характерным свойством центральной

симметрии, а именно, справедливо обратное утверждение, являющееся признаком центральной

симметрии: "Движение, изменяющее направления на противоположные, является центральной симметрией."

Слайд 12 Задача:
Докажите, что

Задача:Докажите, что при центральной симметрии:а)прямая, не приходящая через

при центральной симметрии:
а)прямая, не приходящая через центр симметрии, отображается

на параллельную ей прямую;
б)прямая, проходящая через центр симметрии, отображается на себя.

Слайд 13 Заключение
Симметрию можно обнаружить почти везде, если знать, как

Заключение Симметрию можно обнаружить почти везде, если знать, как ее искать. Многие

ее искать. Многие народы с древнейших времен владели представлением

о симметрии в широком смысле – как об уравновешенности и гармонии. Творчество людей во всех своих проявлениях тяготеет к симметрии. Посредством симметрии человек всегда пытался, по словам немецкого математика Германа Вейля, «постичь и создать порядок, красоту и совершенство».