- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Понятия стереометрии
Содержание
- 2. В аксиомах стереометрии выражены основные свойства неопределяемых
- 3. Система аксиом состоит из аксиом
- 4. Аксиома от греч. axíõma – принятие положенияисходное положение научной теории, принимаемое без доказательства
- 5. Аксиомы планиметрии1. Каждой прямой принадлежат по крайней
- 6. Аксиомы стереометрииА1. Через любые три точки, не
- 7. Ясно, что в каждой плоскости лежат какие-то
- 8. Аксиома 1. В пространстве существуют плоскости. Через
- 9. Иллюстрации к аксиоме А1 из жизни.Табурет с
- 10. ОАВПостроение прямых углов на местности с помощьюпростейшего прибора, который называется экер Треножник с экером.
- 11. Через три точки
- 12. Через три точки
- 13. Через три точки
- 14. Аксиома1Через любые три точки , не лежащие
- 15. aА2. Если две точки прямой лежат в
- 16. Свойство, выраженное в аксиоме А2, используется для
- 17. Аксиома2 Если две точки прямой лежат
- 18. Из аксиомы А2 следует, что если прямая
- 19. aА3. Если две плоскости имеют общую точку,
- 20. Если две различные плоскости имеют общую точку,
- 22. Аксиома3 Если две плоскости имеют общую точку,
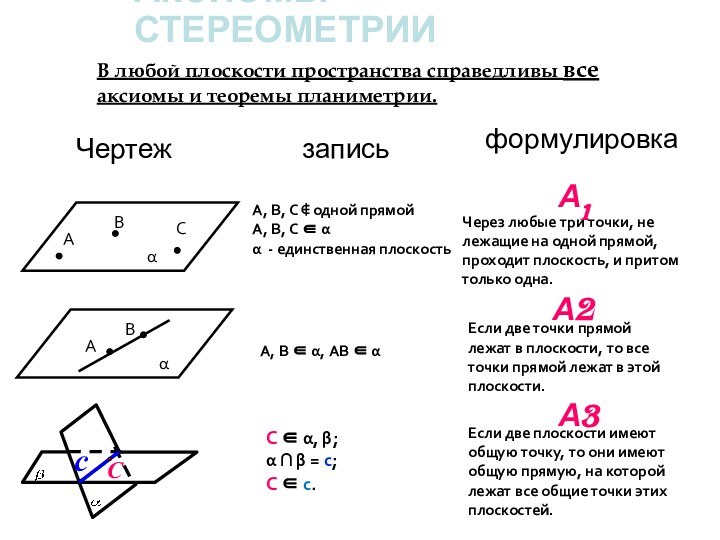
- 23. А1. Через любые три точки, не
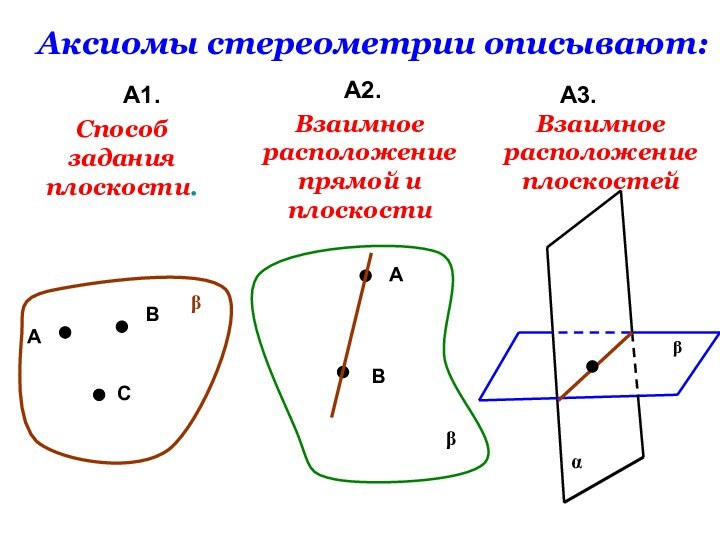
- 24. Аксиомы стереометрии описывают:А1.А2. А3. АВСbСпособ задания плоскости.bАВВзаимное расположение прямой и плоскостиabВзаимное расположение плоскостей
- 25. Скачать презентацию
- 26. Похожие презентации














Слайд 2 В аксиомах стереометрии выражены основные свойства неопределяемых понятий:
точки, прямой, плоскости и расстояния.
Слайд 3
Система аксиом состоит из аксиом
планиметрии
и стереометрииВ планиметрии характеризуется взаимное расположение точек и прямых на плоскости.
В стереометрии характеризуется взаимное расположение точек, прямых, плоскостей в пространстве.
Слайд 4
Аксиома
от греч. axíõma – принятие положения
исходное положение
научной теории, принимаемое без доказательства
Слайд 5
Аксиомы планиметрии
1. Каждой прямой принадлежат по крайней мере
две точки
2. Имеются по крайней мере три точки,
не лежащие на одной прямой3. Через любые две точки проходит прямая, и притом только одна.
Слайд 6
Аксиомы стереометрии
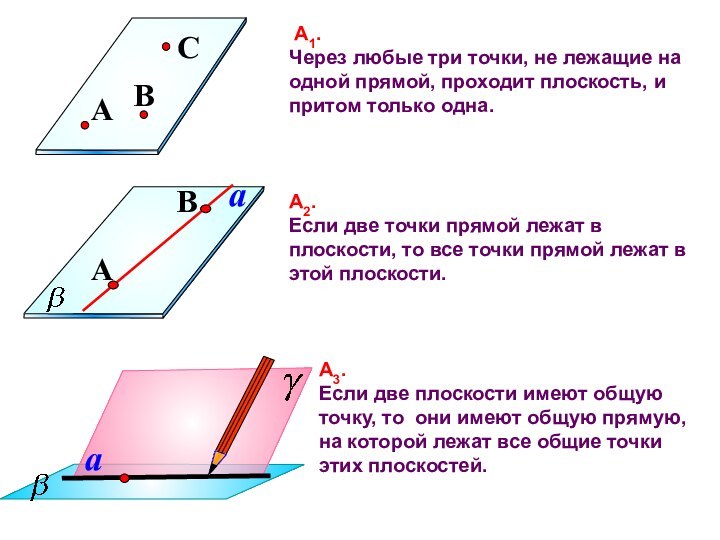
А1. Через любые три точки, не лежащие
на одной прямой, проходит плоскость, и притом только одна
А2.
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскостиА3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
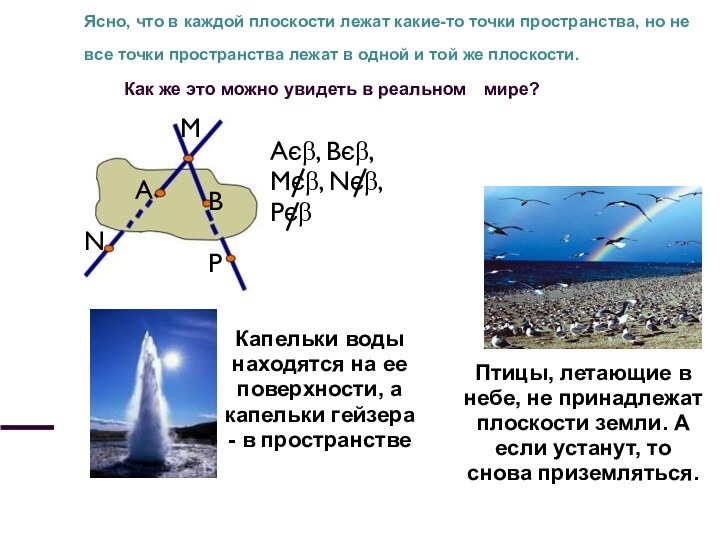
Слайд 7 Ясно, что в каждой плоскости лежат какие-то точки
пространства, но не все точки пространства лежат в одной
и той же плоскости.Как же это можно увидеть в реальном мире?
Капельки воды находятся на ее поверхности, а капельки гейзера - в пространстве
Птицы, летающие в небе, не принадлежат плоскости земли. А если устанут, то снова приземляться.
Aє, Bє,
Mє, Nє, Pє
Слайд 8
Аксиома 1.
В пространстве существуют плоскости.
Через каждые
три точки пространства проходит плоскость.
АКСИОМЫ
М и М;
{А,
В, С}M | {А, В, С} Вопросы
1) Зачем первая часть аксиомы при наличии второй?
Каким утверждением ее можно было заменить?
2) Является ли множество М конечным или бесконечным?
3) Верно ли, что через каждые одну или две точки
пространства проходит плоскость?
4) Докажите, что в пространстве через каждые две точки
проходит прямая.
Следует ли отсюда, что прямые в пространстве можно
обозначать (AB), (CD), ..., как в планиметрии?
Слайд 9
Иллюстрации к аксиоме А1 из жизни.
Табурет с тремя
ножками всегда идеально встанет на пол и не будет
качаться. У табурета с четырьмя ножками бывают проблемы с устойчивостью, если ножки стула не одинаковые по длине. Табурет качается, т. е. опирается на три ножки, а четвертая ножка (четвертая «точка») не лежит в плоскости пола, а висит в воздухе.Для видеокамеры, фотосъемки и для других приборов часто используют штатив – треногу. Три ножки штатива устойчиво расположатся на любом полу в помещениях, на асфальте или прямо на газоне на улице, на песке на пляже или в траве в лесу. Три ножки штатива всегда найдут плоскость.
Слайд 10
О
А
В
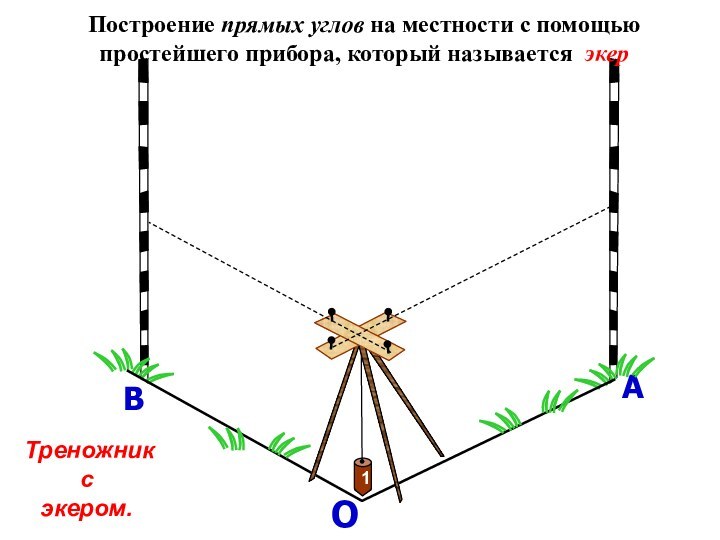
Построение прямых углов на местности с помощью
простейшего
прибора, который называется экер
Треножник
с
экером.
Слайд 14
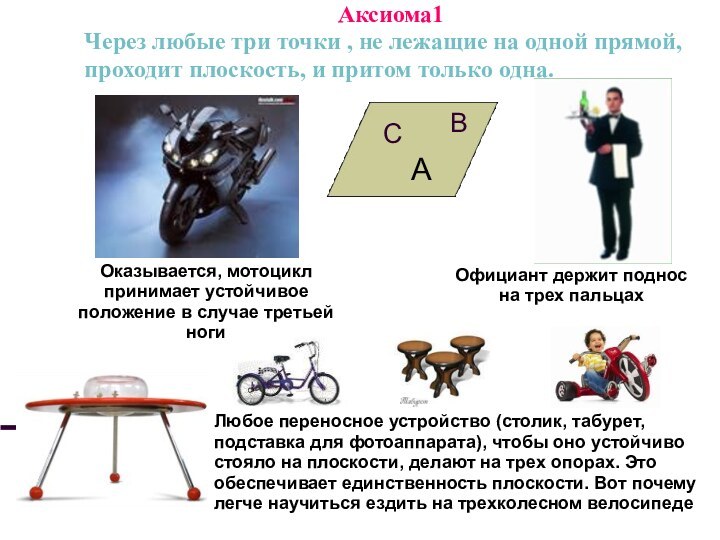
Аксиома1
Через любые три точки , не лежащие на
одной прямой, проходит плоскость, и притом только одна.
Оказывается, мотоцикл
принимает устойчивое положение в случае третьей ногиОфициант держит поднос на трех пальцах
Любое переносное устройство (столик, табурет, подставка для фотоаппарата), чтобы оно устойчиво стояло на плоскости, делают на трех опорах. Это обеспечивает единственность плоскости. Вот почему легче научиться ездить на трехколесном велосипеде
А
В
С
Слайд 15
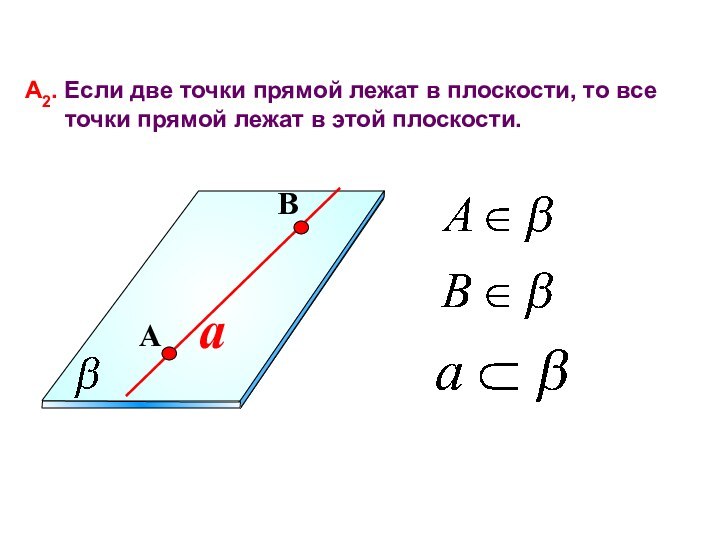
a
А2. Если две точки прямой лежат в плоскости,
то все
точки прямой лежат в этой
плоскости. A
B
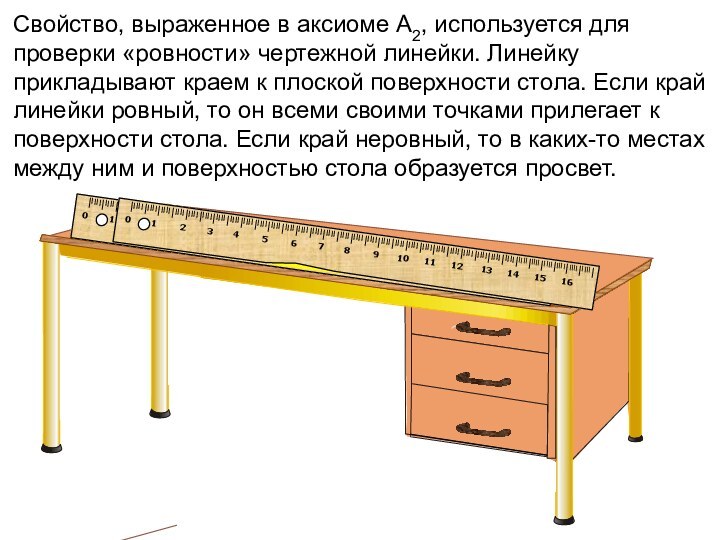
Слайд 16 Свойство, выраженное в аксиоме А2, используется для проверки
«ровности» чертежной линейки. Линейку прикладывают краем к плоской поверхности
стола. Если край линейки ровный, то он всеми своими точками прилегает к поверхности стола. Если край неровный, то в каких-то местах между ним и поверхностью стола образуется просвет.Слайд 17 Аксиома2 Если две точки прямой лежат в плоскости,
то все точки прямой лежат в этой плоскости
Поэтому можно
развешивать на стенах картины или другие предметы. По принципу этой аксиомы происходит размещение вещей на вешалкахА
В
С
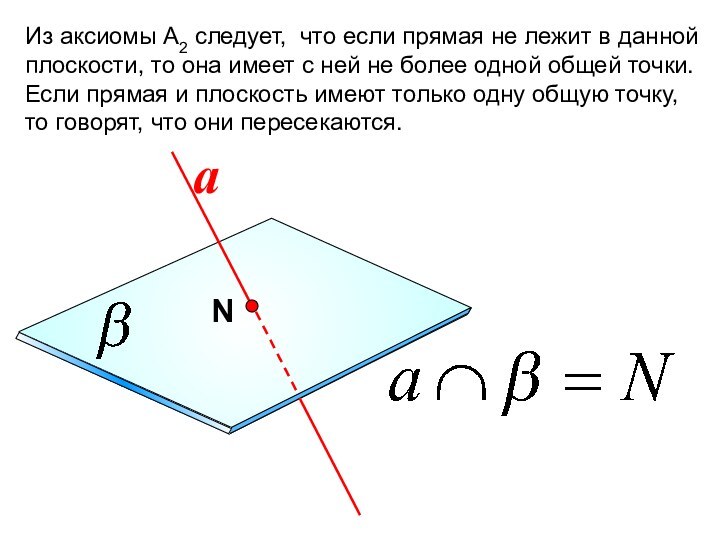
Слайд 18 Из аксиомы А2 следует, что если прямая не
лежит в данной плоскости, то она имеет с ней
не более одной общей точки. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются.
Слайд 19
a
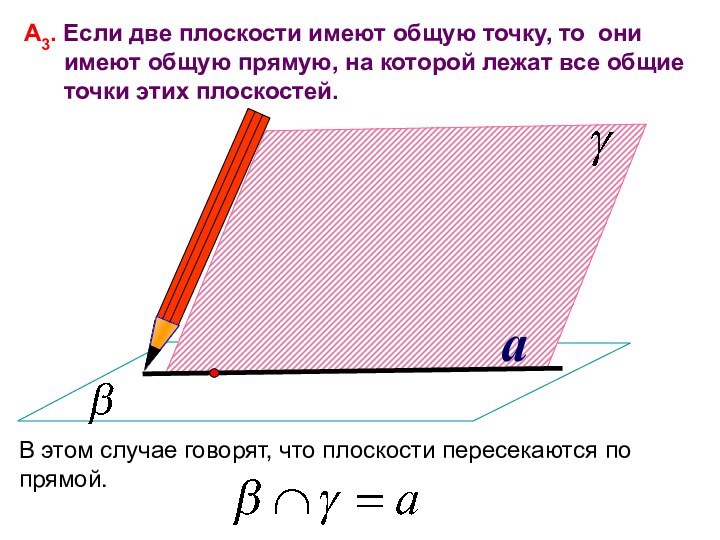
А3. Если две плоскости имеют общую точку, то
они
имеют общую прямую, на которой лежат
все общиеточки этих плоскостей.
В этом случае говорят, что плоскости пересекаются по прямой.
Слайд 20
Если две различные плоскости имеют общую точку,
то
их пересечением является прямая.
Аксиома 2.
С, С
= c Почему Сс?
Определение.
Две различные плоскости, имеющие общую точку,
называются пересекающимися.
1)Докажите, что X
2)Докажите существование пересекающихся плоскостей
Определение.
Сечением фигуры F плоскостью называется их пересечение.
Слайд 21
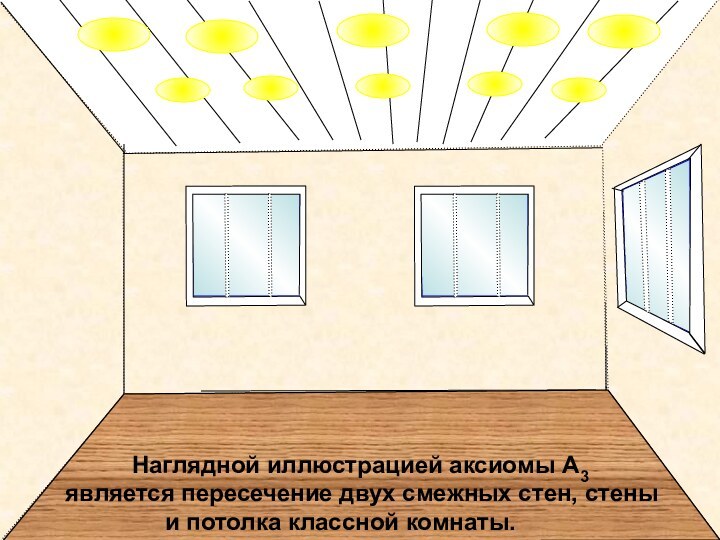
Наглядной иллюстрацией аксиомы А3
является пересечение двух смежных стен, стены и потолка классной комнаты.
Слайд 22 Аксиома3 Если две плоскости имеют общую точку, то они
имеют прямую, на которой лежат все общие точки этих
плоскостей.а
α
А
Потому в книге все листы подшиты к одной прямой, а двери, висячие на петлях, можно открывать
Получили, что через прямую можно провести множество плоскостей.