- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Построение и анализ параллельных алгоритмов
Содержание
- 2. Модель PRAMМодель PRAM: Parallel Random-Access MemoryПозволяет учитывать
- 3. Модель PRAMПроцессоры П0, П1, …, Пp–1 используют
- 4. Модель PRAMОдин шаг (такт) работы PRAM-машины синхронизирован по фазам:Чтение данных из памяти.Обработка данных.Запись результата в память.
- 5. Режимы чтения и записиРежимы чтения данных из
- 6. Варианты одновременной записиОдновременная запись одинакового значенияПроизвольная запись:
- 7. Виды PRAM машин и алгоритмов
- 8. ЗАДАЧА НАХОЖДЕНИЯ КОРНЕЙ ДВОИЧНОГО ЛЕСАПример CREW-алгоритма
- 9. Пример CREW-алгоритмаДано: Лес, состоящий из бинарных деревьев.
- 10. Пример CREW-алгоритмаПредставление входных данных:вершины пронумерованы, ребра деревьев
- 11. Пример CREW-алгоритмаРезультат работы алгоритма — массив root.
- 12. CREW-алгоритмДля каждого процессора Pi выполнить
- 13. Анализ CREW-алгоритмаВременная сложность алгоритма: O(log2 d), где
- 14. НАХОЖДЕНИЕ МАКСИМАЛЬНОГО ЭЛЕМЕНТА В МАССИВЕПример CRCW-алгоритма
- 15. Пример CRCW-алгоритмаДано: Массив n элементовТребуется: Найти максимальный элемент
- 16. Пример CRCW-алгоритмаСпособ решенияКоличество процессоров: n2. Каждый процессор
- 17. CRCW-алгоритмДля всех i от 0 до n–1
- 18. Анализ CRCW-алгоритмаБез использования параллельного чтения невозможно решить
- 19. Скачать презентацию
- 20. Похожие презентации
Модель PRAMМодель PRAM: Parallel Random-Access MemoryПозволяет учитывать ограничения, связанные с одновременным доступом к памятиЯвляется идеализированной моделью архитектуры SMP (Symmetric MultiProcessor, Shared Memory Processor)
![Пример CREW-алгоритмаРезультат работы алгоритма — массив root. В ячейке root[i] хранится вершины,](/img/tmb/15/1437251/3884ce732d7fdfa566cc58c13d86ec53-720x.jpg "Построение и анализ параллельных алгоритмов")
![CREW-алгоритмДля каждого процессора Pi выполнить Если parent[i] = NIL, то](/img/tmb/15/1437251/af552d2ddcb094d8d31d93b5ddab8064-720x.jpg "Построение и анализ параллельных алгоритмов")
![CRCW-алгоритмДля всех i от 0 до n–1 выполнить: m[i] := true;Для всех](/img/tmb/15/1437251/8824cd2a4a03ef7338d3c07c8238867f-720x.jpg "Построение и анализ параллельных алгоритмов")
Слайд 2
Модель PRAM
Модель PRAM: Parallel Random-Access Memory
Позволяет учитывать ограничения,
связанные с одновременным доступом к памяти
SMP (Symmetric MultiProcessor, Shared Memory Processor)
Слайд 3
Модель PRAM
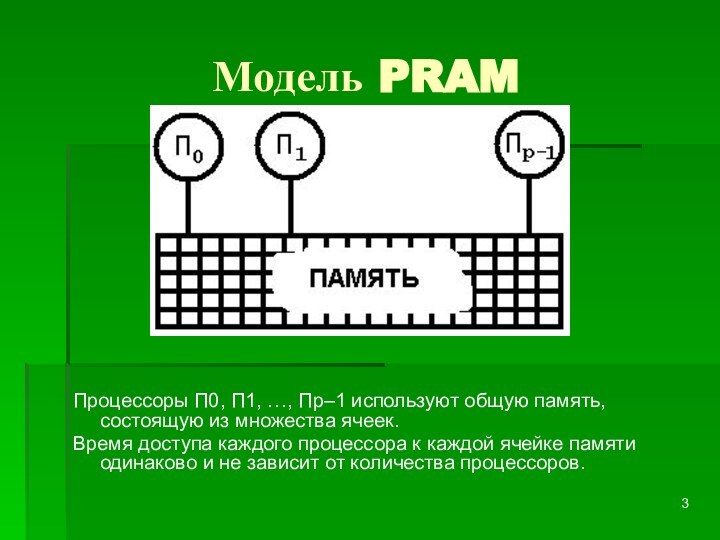
Процессоры П0, П1, …, Пp–1 используют общую
память, состоящую из множества ячеек.
Время доступа каждого процессора
к каждой ячейке памяти одинаково и не зависит от количества процессоров.
Слайд 4
Модель PRAM
Один шаг (такт) работы PRAM-машины синхронизирован по
фазам:
Чтение данных из памяти.
Обработка данных.
Запись результата в память.
Слайд 5
Режимы чтения и записи
Режимы чтения данных из памяти:
Одновременное
(Concurrent Read)
Исключающее (Exclusive Read)
Режимы записи в память:
Одновременная (Concurrent Write)
Исключающая
(Exclusive Write)
Слайд 6
Варианты одновременной записи
Одновременная запись одинакового значения
Произвольная запись: сохраняется
произвольное значение из множества записываемых
Запись в зависимости от приоритетов
процессоровКомбинация записываемых значений
Слайд 9
Пример CREW-алгоритма
Дано: Лес, состоящий из бинарных деревьев. Деревья
заданы следующим образом: для каждой вершины имеется указатель на
её родителя. Для корней деревьев этот указатель пуст.Требуется: для каждой вершины найти корень дерева, которому она принадлежит
Слайд 10
Пример CREW-алгоритма
Представление входных данных:
вершины пронумерованы,
ребра деревьев заданы
с помощью массива parent: элемент parent[i] представляет номер вершины,
являющейся родителем для вершины с номером i.
Слайд 11
Пример CREW-алгоритма
Результат работы алгоритма — массив root. В
ячейке root[i] хранится вершины, являющейся корнем дерева, в которое
входит вершина i.Массивы parent и root хранятся в общей памяти.
Слайд 12
CREW-алгоритм
Для каждого процессора Pi выполнить
Если
parent[i] = NIL, то root[i] := i;
Пока существует узел
i, для которого parent[i] ≠ NIL, выполнять:Для каждого процессора i выполнить
Если parent[i] ≠ NIL, то
{
root[i] := root[parent[i]];
parent[i] := parent[parent[i]];
}
Слайд 13
Анализ CREW-алгоритма
Временная сложность алгоритма:
O(log2 d),
где d
— наибольшая глубина дерева в заданном лесе.
Можно показать, что
ни один EREW-алгоритм не может решить эту задачу за время, меньшее O(log2 n), где n — количество вершин в лесе
Слайд 16
Пример CRCW-алгоритма
Способ решения
Количество процессоров: n2.
Каждый процессор нумеруется
парой индексов.
Процессор с номером (i,j) сравнивает A[i] и A[j].
Используется вспомогательный булевский массив m[i]. После выполнения сравнений m[i]=true ⇔ A[i] — наибольший элемент массива.
Результат помещается в переменную max.
Слайд 17
CRCW-алгоритм
Для всех i от 0 до n–1 выполнить:
m[i] := true;
Для всех i от 0 до n–1
и для всех j от 0 до n–1 выполнить:Если A[i] < A[j], то m[i] := false;
Для всех i от 0 до n–1 выполнить:
Если m[i] = true, то max := A[i];
Вернуть max.
Слайд 18
Анализ CRCW-алгоритма
Без использования параллельного чтения невозможно решить эту
