- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему поворот и параллельный перенос
Содержание
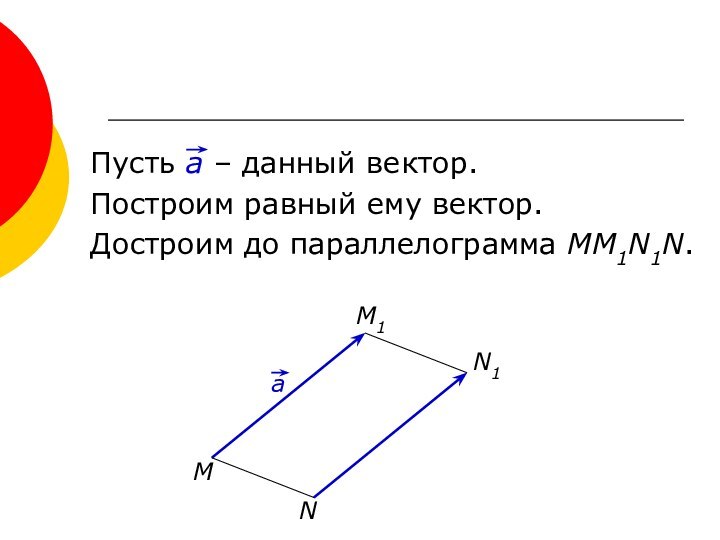
- 2. Пусть а – данный вектор.Построим равный ему вектор.Достроим до параллелограмма ММ1N1N.MM1NN1
- 3. Параллельный переносТаким образом: Параллельным переносом на
- 4. Параллельный перенос является движением, т.е. отображением
- 5. Значит, расстояние между векторами и
- 6. Свойства параллельного переноса:Параллельный перенос перемещает каждую точку
- 7. Дан угол ABC и прямая l. Параллельно
- 8. С помощью циркуля и линейки постройте хорду данной окружности, равную и параллельную данному отрезкуOABc
- 9. Скачать презентацию
- 10. Похожие презентации
Пусть а – данный вектор.Построим равный ему вектор.Достроим до параллелограмма ММ1N1N.MM1NN1







Слайд 3
Параллельный перенос
Таким образом:
Параллельным переносом на вектор
а называется отображение плоскости на себя, при котором каждая
точка М отображается в такую точку М1, что вектор ММ1 равен вектору аСлайд 4 Параллельный перенос является движением, т.е. отображением плоскости на
себя, сохраняющим расстояние
Доказательство:
Пусть при параллельном переносе на
вектор а точки M и N отображаются в точки M1 и N1.Так как все векторы равны.
Следовательно:
Векторы параллельны и равны, а значит четырехугольник ММ1N1N – параллелограмм.
Слайд 5 Значит, расстояние между векторами и точками
равно.
Таким образом, параллельный перенос сохраняет расстояние между
точками и поэтому представляет собой движение.Вывод:
Слайд 6
Свойства параллельного переноса:
Параллельный перенос перемещает каждую точку фигуры
или пространства на одно и то же расстояние в
одном и том же направлении.При параллельном переносе прямая переходит либо в себя, либо в параллельную ей прямую.
Параллельный перенос задается парой соответствующих точек, т.е. каковы бы ни были точки, существует единственный параллельный перенос, при котором точка переходит в точку.
Слайд 7 Дан угол ABC и прямая l. Параллельно прямой
l с помощью циркуля и линейки проведите прямую, на
которой стороны угла ABC высекают отрезок, равный данному.A
B
C
l