с одним и тем же числом сторон
и в
каждой вершине которого сходится одно и то же число ребер.Гексаэдр
Тетраэдр
Октаэдр
Додекаэдр
Икосаэдр
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть















Гексаэдр
Тетраэдр
Октаэдр
Додекаэдр
Икосаэдр
ТЕТРАЭДР
КУБ (ГЕКСАЭДР)
ОКТАЭДР
ИКОСАЭДР
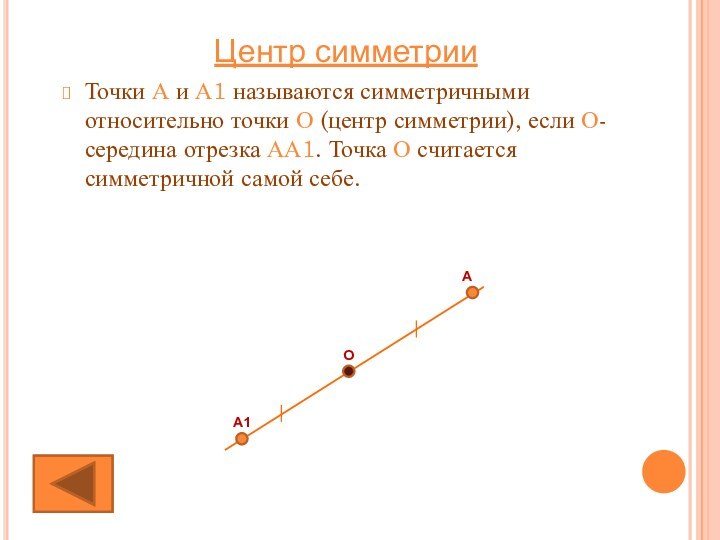
Центр симметрии
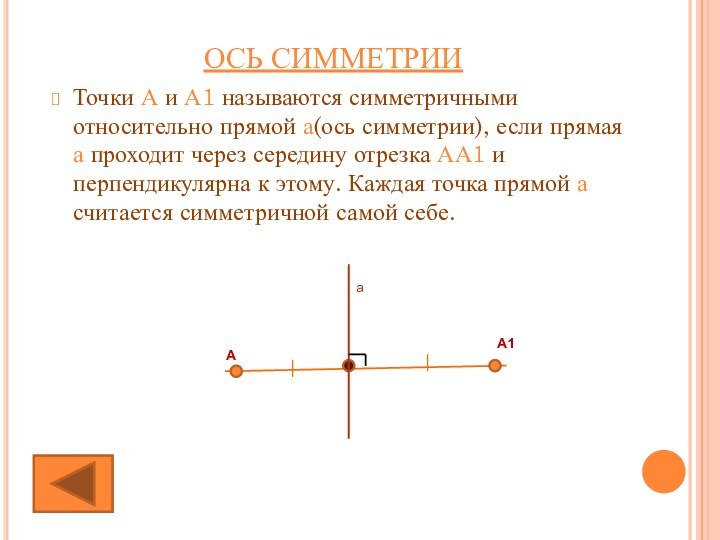
Ось симметрии
Плоскость симметрии
Центр симметрии
А
А
а
А1
α
А
А1