Слайд 2
Правильный многогранник или платоново тело — это выпуклый
многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной
симметрией.
Многогранник называется правильным, если:
1.он выпуклый;
2.все его грани являются равными правильными многоугольниками;
3.в каждой его вершине сходится одинаковое число рёбер.
Слайд 4
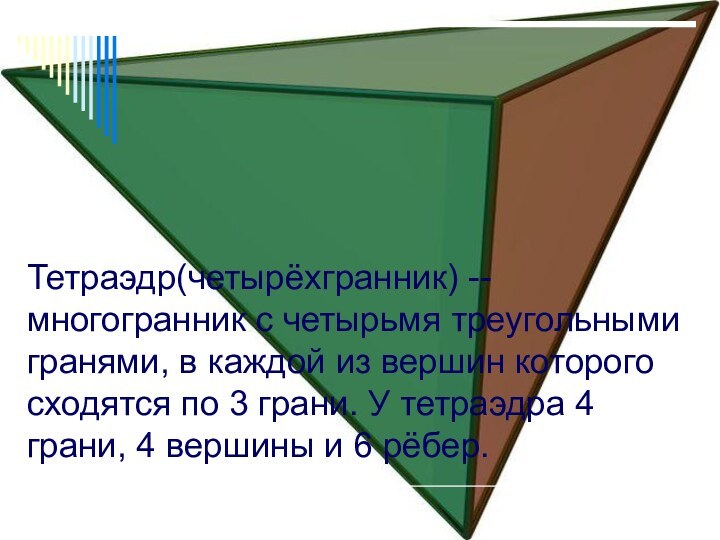
Тетраэдр(четырёхгранник) -- многогранник с четырьмя треугольными гранями, в
каждой из вершин которого сходятся по 3 грани. У
тетраэдра 4 грани, 4 вершины и 6 рёбер.
Слайд 5
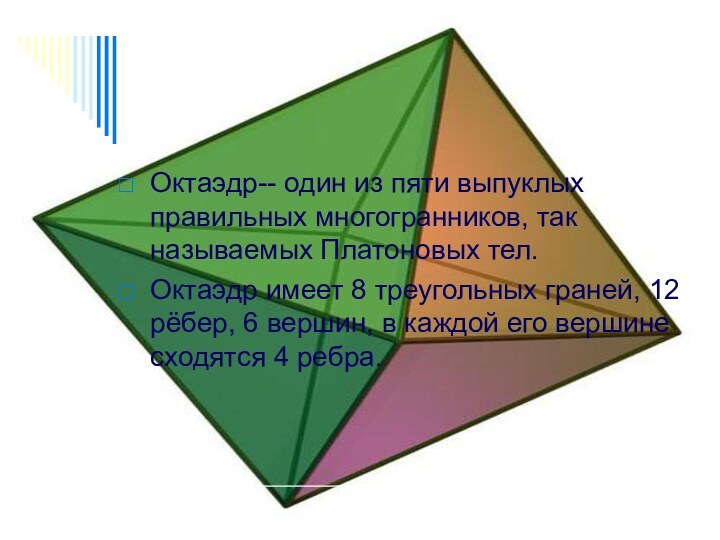
Октаэдр-- один из пяти выпуклых правильных многогранников, так
называемых Платоновых тел.
Октаэдр имеет 8 треугольных граней, 12
рёбер, 6 вершин, в каждой его вершине сходятся 4 ребра.
Слайд 6
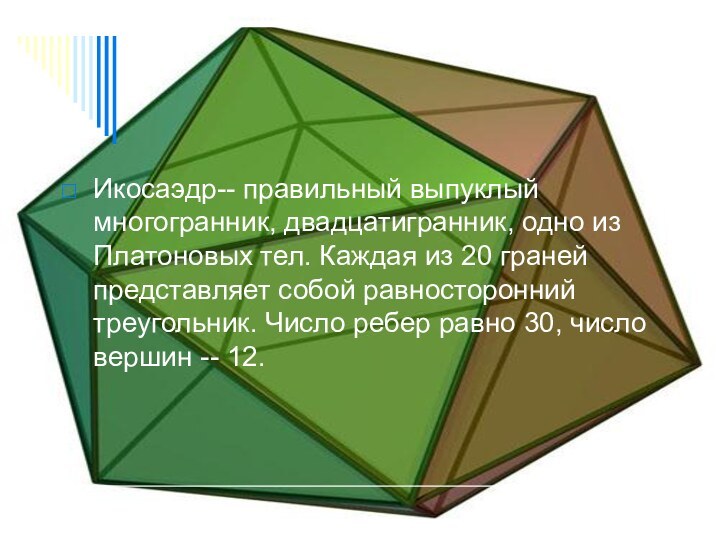
Икосаэдр-- правильный выпуклый многогранник, двадцатигранник, одно из Платоновых
тел. Каждая из 20 граней представляет собой равносторонний треугольник.
Число ребер равно 30, число вершин -- 12.
Слайд 7
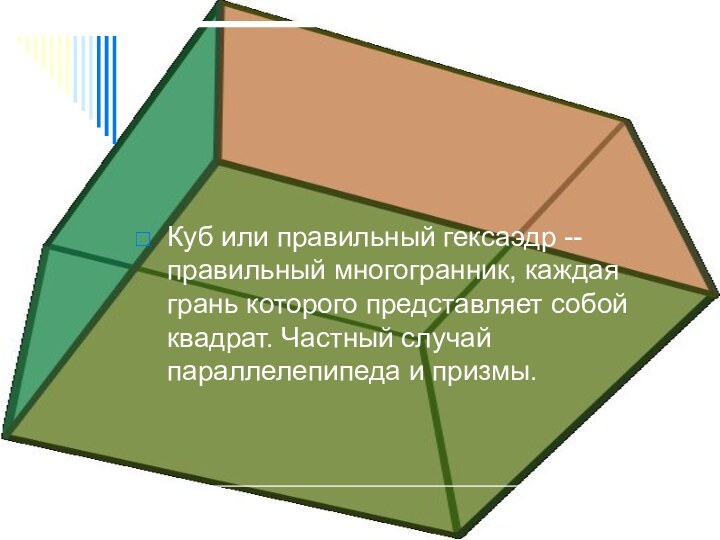
Куб или правильный гексаэдр -- правильный многогранник, каждая
грань которого представляет собой квадрат. Частный случай параллелепипеда и
призмы.
Слайд 8
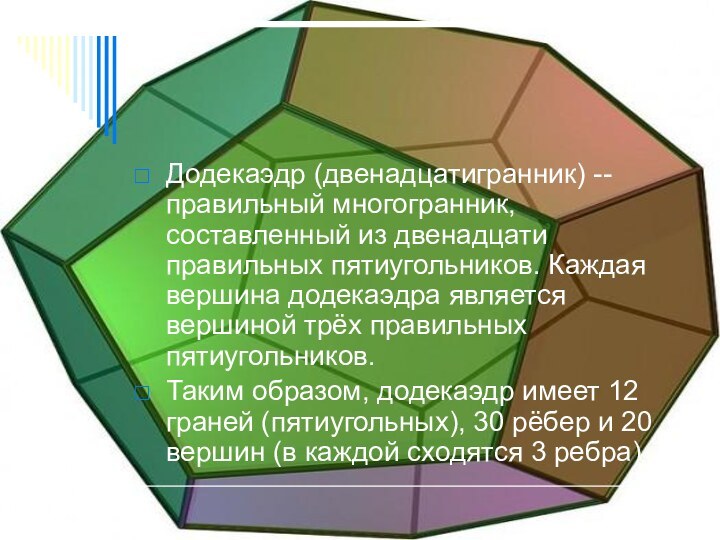
Додекаэдр (двенадцатигранник) -- правильный многогранник, составленный из двенадцати
правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных
пятиугольников.
Таким образом, додекаэдр имеет 12 граней (пятиугольных), 30 рёбер и 20 вершин (в каждой сходятся 3 ребра)
Слайд 9
Геометрические свойства
Площадь поверхности S правильного многогранника {p, q}
вычисляется, как площадь правильного p-угольника, умноженная на число граней
Г:
Объём правильного многогранника вычисляется, как умноженный на число граней объём правильной пирамиды, основанием которой служит правильный p-угольник, а высотой — радиус вписанной сферы r:
Слайд 10
История
Правильные многогранники известны с древнейших времён. Их орнаментные
модели можно найти на резных каменных шарах, созданных в
период позднего неолита, в Шотландии, как минимум за 1000 лет до Платона. В костях, которыми люди играли на заре цивилизации, уже угадываются формы правильных многогранников.
Слайд 11
В значительной мере правильные многогранники были изучены древними
греками. Некоторые источники (такие как Прокл Диадох) приписывают честь
их открытия Пифагору. Другие утверждают, что ему были знакомы только тетраэдр, куб и додекаэдр, а честь открытия октаэдра и икосаэдра принадлежит Теэтету Афинскому, современнику Платона. В любом случае, Теэтет дал математическое описание всем пяти правильным многогранникам и первое известное доказательство того, что их ровно пять.
Слайд 12
Правильные многогранники характерны для философии Платона, в честь

которого и получили название «платоновы тела». Платон писал о
них в своём трактате Тимей (360г до н. э.), где сопоставил каждую из четырёх стихий (землю, воздух, воду и огонь) определённому правильному многограннику. Земля сопоставлялась кубу, воздух — октаэдру, вода — икосаэдру, а огонь — тетраэдру. Для возникновения данных ассоциаций были следующие причины: жар огня ощущается чётко и остро (как маленькие тетраэдры); воздух состоит из октаэдров: его мельчайшие компоненты настолько гладкие, что их с трудом можно почувствовать; вода выливается, если её взять в руку, как будто она сделана из множества маленьких шариков (к которым ближе всего икосаэдры); в противоположность воде, совершенно непохожие на шар кубики составляют землю, что служит причиной тому, что земля рассыпается в руках, в противоположность плавному току воды. По поводу пятого элемента, додекаэдра, Платон сделал смутное замечание: «…его бог определил для Вселенной и прибегнул к нему в качестве образца»
Слайд 13
Евклид дал полное математическое описание правильных многогранников в
последней, XIII книге Начал. Предложения 13—17 этой книги описывают
структуру тетраэдра, октаэдра, куба, икосаэдра и додекаэдра в данном порядке. Для каждого многогранника Евклид нашёл отношение диаметра описанной сферы к длине ребра. В 18-м предложении утверждается, что не существует других правильных многогранников.
Слайд 14
В XVI веке немецкий астроном Иоганн Кеплер пытался
найти связь между пятью известными на тот момент планетами
Солнечной системы (исключая Землю) и правильными многогранниками. В «Тайне мира», опубликованной в 1596 году, Кеплер изложил свою модель Солнечной системы. В ней пять правильных многогранников помещались один в другой и разделялись серией вписанных и описанных сфер. Каждая из шести сфер соответствовала одной из планет (Меркурию, Венере, Земле, Марсу, Юпитеру и Сатурну). Многогранники были расположены в следующем порядке (от внутреннего к внешнему): октаэдр, за ним икосаэдр, додекаэдр, тетраэдр и, наконец, куб. Таким образом, структура Солнечной системы и отношения расстояний между планетами определялись правильными многогранниками.
Слайд 15
Многогранники в природе
Правильные многогранники – самые выгодные фигуры,
поэтому они широко распространены в природе. Подтверждением тому служит
форма некоторых кристаллов
Шеелит (пирамида)
Хрусталь (призма)
Поваренная соль (куб)
Алмаз (октаэдр)