- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Правило суммы. Правило произведения.
Содержание
- 2. Два уровня решения комбинаторных задач.1. Найти хотя
- 3. Два уровня решения комбинаторных задач.2. Если решений много, то посчитать их количество и выбрать оптимальное .
- 4. Сколько человек участвовало в прогулке, если известно,
- 5. В отделе научно – исследовательского института работают
- 6. Киев Чернигов Новгород – Сиверский
- 7. Сколько четырехзначных чисел можно составить из цифр
- 8. Из 33 букв русского алфавита составить все
- 9. Размещения с повторениями.m элементов ( 33 буквы
- 10. Есть конфеты 9 видов. Сколько различных наборов по 5 конфет можно составить ?
- 11. № 422.Сколько существует пятизначных номеров, не содержащих
- 12. Размещения без повторений.A km=____m!( m – k ) !
- 13. № 426.Сколькими способами можно составить трехцветный флаг,
- 14. Перестановки .Permutation ( фр .) – перестановки
- 15. Скачать презентацию
- 16. Похожие презентации
Два уровня решения комбинаторных задач.1. Найти хотя бы одно решение или доказать, что его нет.Если в n клетках сидит n+1 или больше кроликов, то найдётся клетка, в которой сидят по крайней мере два кролика.














Слайд 2
Два уровня решения комбинаторных задач.
1. Найти хотя бы
одно решение или доказать, что его нет.
клетках сидит n+1 или больше кроликов, то найдётся клетка, в которой сидят по крайней мере два кролика.
Слайд 3
Два уровня решения комбинаторных задач.
2. Если решений много,
то посчитать их количество и выбрать оптимальное .
Слайд 4
Сколько человек участвовало в прогулке, если известно,
16
из них взяли бутерброд с ветчиной,
24 – с
колбасой, 15 – с сыром,
11 – с ветчиной и колбасой,
8 – с ветчиной и сыром,
12 – с колбасой и сыром,
6 человек – бутерброды всех видов и
6 человек взяли пирожки.
Слайд 5 В отделе научно – исследовательского института работают несколько
человек, причем каждый из них знает хотя бы один
иностранный язык:6 человек знают английский язык,
6 – немецкий, 7 – французский ,
4 – английский и немецкий,
3 – немецкий и французский,
2 – французский и английский,
1 человек знает все три языка.
Сколько человек работают в отделе? Сколько из них знает только английский язык?
Сколько человек знают только один язык?
Слайд 7 Сколько четырехзначных чисел можно составить из цифр 0,1,2,3,4.5,
если :
а) ни одна цифра не повторяется;
б) цифры могут
повторяться;в) число нечетное и цифры могут повторяться.
Слайд 8 Из 33 букв русского алфавита составить все возможные
слова, состоящие из
2 – х букв,
из 3
– букв.
Слайд 9
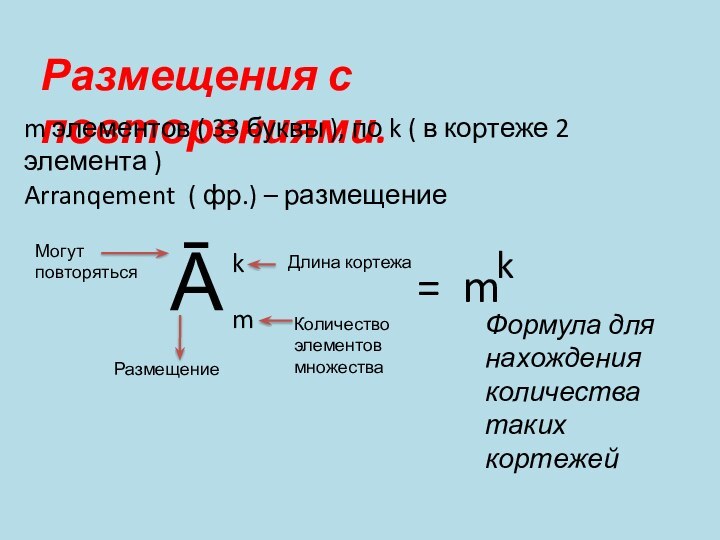
Размещения с повторениями.
m элементов ( 33 буквы ),
по k ( в кортеже 2 элемента )
Arranqement (
фр.) – размещение Ā
m
k
Могут
повторяться
Длина кортежа
Количество
элементов
множества
Размещение
=
m
k
Формула для нахождения количества таких кортежей
Слайд 11
№ 422.
Сколько существует пятизначных номеров, не содержащих цифру
8?
Не содержащих цифры 8 и 0 ?
Составленных из цифр
2,3,5,7?
Слайд 13
№ 426.
Сколькими способами можно составить трехцветный флаг, если
имеются ткани пяти различных цветов?
Решите эту задачу при условии,
что одна полоса должна быть красной.№ 428.
Из 10 различных книг выбирают 4 для посылки. Сколькими способами это можно сделать?