такое Бесконечность?
Предел функции на бесконечности
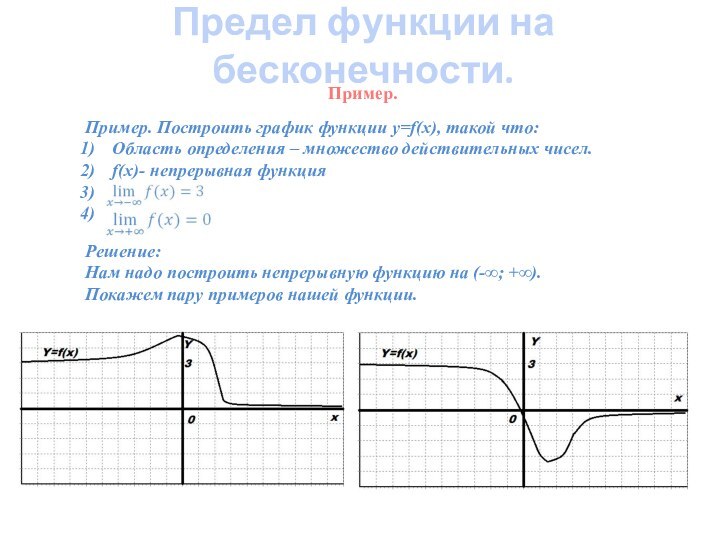
Примеры.
Предел функции на плюс бесконечности.
Предел
функции на минус бесконечности.Свойства.