Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Плоскость и прямая в пространстве

Содержание

2. Определение. Уравнением поверхности в пространстве
3. Назовем нормалью к плоскости вектор, перпендикулярный к этой плоскости. Обозначают нормаль
4. Уравнение плоскости, проходящей через заданную точку
5. М
6. общее уравнение плоскости Из предыдущего уравнения легко получить общее уравнение плоскости
7. Частные случаи общего уравнения 1. плоскость проходит
8. Уравнение в отрезках
10. Уравнение плоскости, проходящей через три точки
11. Запишем координаты векторов: Эти векторы компланарны,
12. Уравнение плоскости, проходящей через три точки
13. Взаимное расположение плоскостей
14. Угол между плоскостями Даны две плоскости
15. Условие перпендикулярности плоскостей Если плоскости
16. Условие параллельности плоскостей Если плоскости параллельны друг к другу, то соответственно параллельны их нормальные векторы:
17. Расстояние от точки до плоскости
18. Пример Найти уравнение плоскости, проходящей через точки .
19. Решение В уравнение плоскости, проходящей
20. Прямая в пространстве.
21. M
22. Канонические уравнения прямой.
23. Параметрические уравнения (вывести самостоятельно) t-переменный параметр.
24. Уравнение прямой, проходящей через две точки Точки
25. Общее уравнение прямой Прямая линия в пространстве определяется как линия пересечения двух плоскостей
26. каждое уравнение отдельно- это
27. Пример Записать канонические уравнения прямой,
28. Сложив уравнения, получим
29. Найдем направляющий вектор этой прямой: Получим канонические уравнения прямой
30. Взаимное расположение прямых в пространстве
31. Угол между прямыми Угол между прямыми равен углу между их направляющими векторами
32. Параллельность прямыхЕсли то
33. Перпендикулярность прямых Если то
34. Взаимное расположение прямой и плоскости
35. Угол между прямой и плоскостьюφ
36. Углом между прямой и плоскостью
37. Угол между прямой и плоскостью
38. Условие параллельности прямой и плоскостиЕсли то
39. Условие перпендикулярности прямой и плоскостиЕсли то
40. Точка пересечения прямой и плоскости Пусть
41. Получим уравнение вида относительно
42. Замечание. Если уравнение относительно t
43. ПримерНайти точку пересечения прямой и плоскости
44. Пример Написать уравнение плоскости, проходящей через точки А(1;2;0) и В(2;1;1) перпендикулярно заданной плоскости –х+у-1=0.АВМ
45. Пример Показать, что прямая лежит в плоскости
46. Подставим в уравнение плоскости:
47. Скачать презентацию
48. Похожие презентации

Определение. Уравнением поверхности в пространстве называется такое уравнение между переменными которому удовлетворяют координаты всех точек данной поверхности и не удовлетворяют координаты точек, не

Главная
Математика
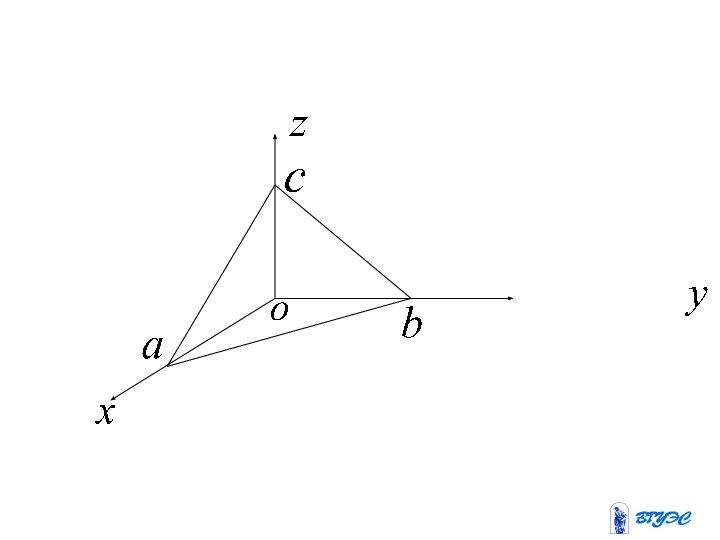
Плоскость и прямая в пространстве

Плоскость и прямая в пространстве Лекция 10

Определение. Уравнением поверхности в пространстве называется

Назовем нормалью к плоскости вектор, перпендикулярный к этой плоскости. Обозначают нормаль

Уравнение плоскости, проходящей через заданную точку Пусть точки

общее уравнение плоскости Из предыдущего уравнения легко получить общее уравнение плоскости

Частные случаи общего уравнения 1. плоскость проходит через начало координат. 2. плоскость

Уравнение в отрезках Перенесем свободный член в правую

Уравнение плоскости, проходящей через три точки

Запишем координаты векторов: Эти векторы компланарны, т.к. лежат в

Угол между плоскостями Даны две плоскости

Условие перпендикулярности плоскостей Если плоскости перпендикулярны друг к другу, то

Условие параллельности плоскостей Если плоскости параллельны друг к другу, то соответственно параллельны их нормальные векторы:

Пример Найти уравнение плоскости, проходящей через точки .

Решение В уравнение плоскости, проходящей через три точки, подставим координаты

Параметрические уравнения (вывести самостоятельно) t-переменный параметр.

Уравнение прямой, проходящей через две точки Точки

Общее уравнение прямой Прямая линия в пространстве определяется как линия пересечения двух плоскостей

каждое уравнение отдельно- это уравнение

Пример Записать канонические уравнения прямой, заданной общими уравнениями

Сложив уравнения, получим Тогда из второго уравнения Точка

Найдем направляющий вектор этой прямой: Получим канонические уравнения прямой

Взаимное расположение прямых в пространстве

Угол между прямыми Угол между прямыми равен углу между их направляющими векторами

Взаимное расположение прямой и плоскости

Углом между прямой и плоскостью называется угол между прямой

Условие параллельности прямой и плоскостиЕсли то

Условие перпендикулярности прямой и плоскостиЕсли то

Точка пересечения прямой и плоскости Пусть требуется найти точку пересечения прямой

Получим уравнение вида относительно параметра t. Выразив t из

Замечание. Если уравнение относительно t примет вид 0t = 0

ПримерНайти точку пересечения прямой и плоскости

Пример Написать уравнение плоскости, проходящей через точки А(1;2;0) и В(2;1;1) перпендикулярно заданной плоскости –х+у-1=0.АВМ

Пример Показать, что прямая лежит в плоскости Решение. Используем параметрические

Подставим в уравнение плоскости: - Получили равенство, верное

Пример Найти уравнение перпендикуляра к плоскости

Слайды презентации

Слайд 2 Определение. Уравнением поверхности в пространстве

Определение. Уравнением поверхности в пространстве называется такое уравнение

называется такое уравнение между переменными

которому удовлетворяют координаты всех точек данной поверхности и не удовлетворяют координаты точек, не лежащих на этой поверхности.

Слайд 3 Назовем нормалью к плоскости вектор, перпендикулярный

к этой плоскости. Обозначают нормаль

Слайд 4 Уравнение плоскости, проходящей через заданную точку
Пусть

Уравнение плоскости, проходящей через заданную точку Пусть точки и

точки и лежат

на плоскости . Тогда и, значит, их скалярное произведение равно нулю:

это уравнение плоскости, проходящей через точку перпендикулярно вектору
.

Слайд 5 М

Слайд 6 общее уравнение плоскости
Из предыдущего

уравнения легко получить общее уравнение плоскости

Слайд 7 Частные случаи общего уравнения
1.
плоскость проходит через

Частные случаи общего уравнения 1. плоскость проходит через начало координат. 2.

начало координат.
2.
плоскость параллельна оси OX.
3.
плоскость

параллельна плоскости XOY.
4.
Плоскость проходит через ось OX.

5.
плоскость является плоскостью XOY.
Остальные случаи рассмотреть самостоятельно.

Слайд 8 Уравнение в отрезках
Перенесем

Уравнение в отрезках Перенесем свободный член в правую часть

свободный член в правую часть уравнения и разделим на

него все слагаемые

Введя соответствующие обозначения , имеем

.

Слайд 9

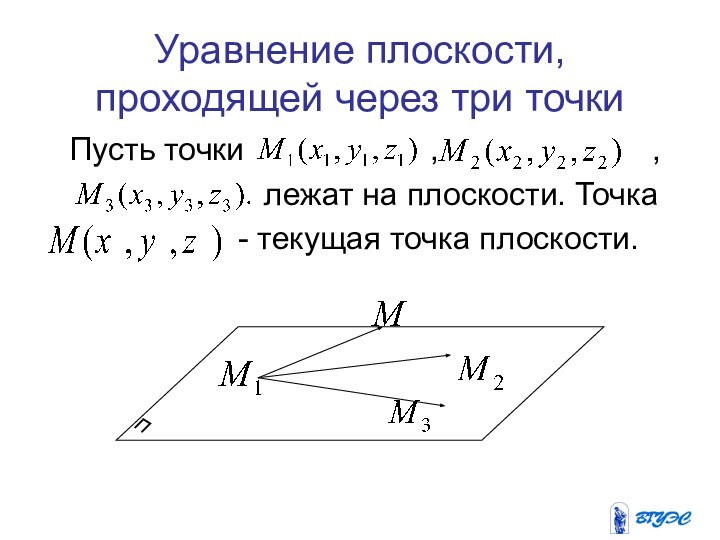
Слайд 10 Уравнение плоскости, проходящей через три точки

Пусть точки , ,
лежат на плоскости. Точка
- текущая точка плоскости.

Слайд 11 Запишем координаты векторов:

Эти векторы компланарны, т.к.

Запишем координаты векторов: Эти векторы компланарны, т.к. лежат в одной

лежат в
одной плоскости. Следовательно

их смешанное произведение равно нулю.
Получаем уравнение:

Слайд 12 Уравнение плоскости, проходящей через три точки

Слайд 13 Взаимное расположение плоскостей

Слайд 14 Угол между плоскостями
Даны две плоскости

и

:

Тогда:

Слайд 15 Условие перпендикулярности плоскостей
Если плоскости перпендикулярны друг

Условие перпендикулярности плоскостей Если плоскости перпендикулярны друг к другу, то соответственно перпендикулярны их нормальные векторы

к другу, то соответственно перпендикулярны их нормальные векторы

Слайд 16 Условие параллельности плоскостей
Если плоскости параллельны друг к

другу, то соответственно параллельны их нормальные векторы:

Слайд 17 Расстояние от точки

до плоскости

Слайд 18 Пример
Найти уравнение плоскости, проходящей через точки

.

Слайд 19 Решение
В уравнение плоскости, проходящей через

три точки, подставим координаты данных точек:

Раскладывая

определитель по элементам первой строки, имеем
.

Слайд 20 Прямая в пространстве.

Слайд 21 M

Слайд 22 Канонические уравнения прямой.

-направляющий вектор

прямой, -точка прямой. Тогда

Слайд 23 Параметрические уравнения (вывести самостоятельно)

t-переменный параметр.

Слайд 24 Уравнение прямой, проходящей через две точки
Точки

и
лежат на прямой. Вывод уравнения сделать самостоятельно.

Слайд 25 Общее уравнение прямой
Прямая линия в

пространстве определяется как линия пересечения двух плоскостей

Слайд 26

каждое уравнение отдельно- это

каждое уравнение отдельно- это уравнение плоскости,

уравнение плоскости, которые

пересекаются по прямой.

Слайд 27 Пример
Записать канонические уравнения прямой, заданной

Пример Записать канонические уравнения прямой, заданной общими уравнениями Решение.

общими уравнениями

Решение. Найдем точку на

прямой. Пусть, например, z = 0. Система примет вид

Слайд 28 Сложив уравнения, получим

Тогда из второго уравнения

Точка на прямой А(1;

-2; 0).

Слайд 29 Найдем направляющий вектор этой прямой:

Получим канонические уравнения прямой

Слайд 30 Взаимное расположение прямых в пространстве

Слайд 31 Угол между прямыми
Угол между прямыми равен углу

между их направляющими векторами

Слайд 32 Параллельность прямых
Если то

Слайд 33 Перпендикулярность прямых

Если

то

Слайд 34 Взаимное расположение прямой и плоскости

Слайд 35 Угол между прямой и плоскостью
φ

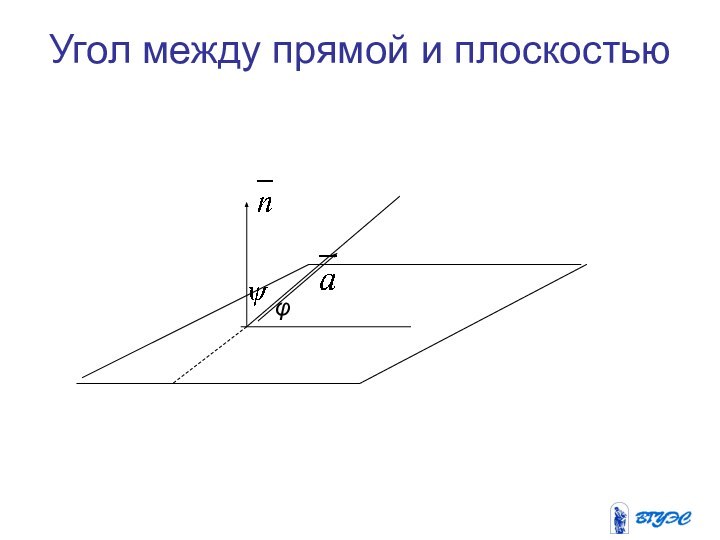
Слайд 36 Углом между прямой и плоскостью

называется угол между прямой и ее
ортогональной проекцией

на плоскость

Слайд 37 Угол между прямой и плоскостью

-нормаль плоскости П,
-направляющий вектор прямой .

Слайд 38 Условие параллельности прямой и плоскости

Если

то

Слайд 39 Условие перпендикулярности прямой и плоскости

Если

то

Слайд 40 Точка пересечения прямой и плоскости
Пусть требуется

найти точку пересечения прямой

и плоскости

Запишем параметрические уравнения прямой

и подставим выражения для х, у, z в уравнение плоскости.

Слайд 41 Получим уравнение вида
относительно

параметра t. Выразив t из этого уравнения и подставив

в параметрические уравнения прямой, найдем координаты точки пересечения прямой и плоскости.

Слайд 42 Замечание. Если уравнение относительно t примет

вид 0t = 0 (то есть M = N

= 0), то любое действительное значение t будет его решением, значит, прямая и плоскость имеют множество общих точек, то есть прямая лежит в плоскости.