- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по алгебре Арксинус. Решение уравнения sin t = a 10 класс
Содержание
- 2. ЦелиИзучить определение арксинуса числа.Изучить формулы решения простейшего тригонометрического уравнения sin t = a.
- 3. ПовторимЧто называется синусом числа t на числовой
- 4. ПовторимРешим простейшее уравнение вида sin t = a с помощью числовой окружности.
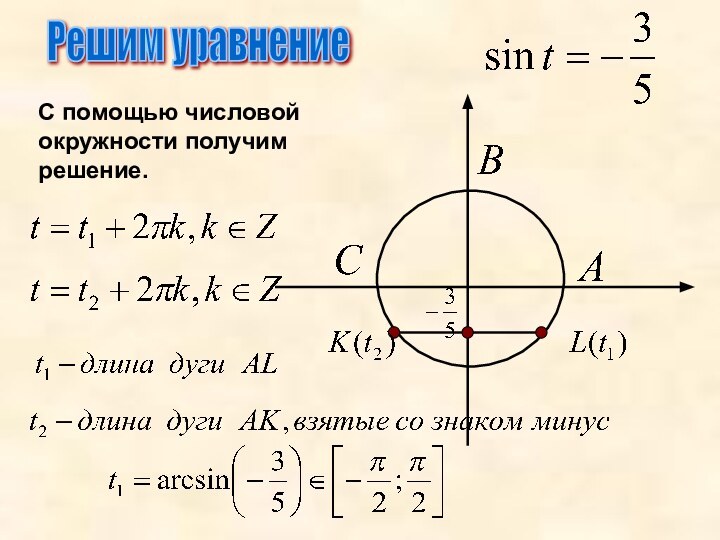
- 5. Решим уравнениеС помощью числовой окружности получим решение.
- 6. ?Решим уравнениеЧто это за число t1?В рассмотрение введён новый символ«арксинус трёх пятых»
- 7. С помощью введённого символа можно записать корни
- 8. Решим уравнениеС помощью числовой окружности получим решение.
- 9. С помощью числовой окружности сравнимДуги AM и AL равны по длине и противоположны по направлению
- 10. Получим
- 11. Определение
- 12. Существует три частных случая решения уравнения sin t = a
- 13. Пример 1.Вычислить:
- 14. Пример 1.Вычислить:
- 15. Дуги АМ и АL равны по модулю и противоположны по направлению.
- 16. Пример 2.Решить уравнение
- 17. Пример 2.Решить уравнение
- 18. Пример 2.Решить уравнение
- 19. Принята общая формула решения тригонометрического уравнения sin t = a
- 20. Пример 3.Решить неравенствоСтроим окружностьУчитываем, что синус –
- 21. Решите из учебника№ 16.1, 16.3, 16.5, 16.9, 16.11
- 22. Задание на дом§ 16 выучить№ 16.2, 16.4, 16.6
- 23. Скачать презентацию
- 24. Похожие презентации
ЦелиИзучить определение арксинуса числа.Изучить формулы решения простейшего тригонометрического уравнения sin t = a.





















Слайд 2
Цели
Изучить определение арксинуса числа.
Изучить формулы решения простейшего тригонометрического
уравнения sin t = a.
Слайд 3
Повторим
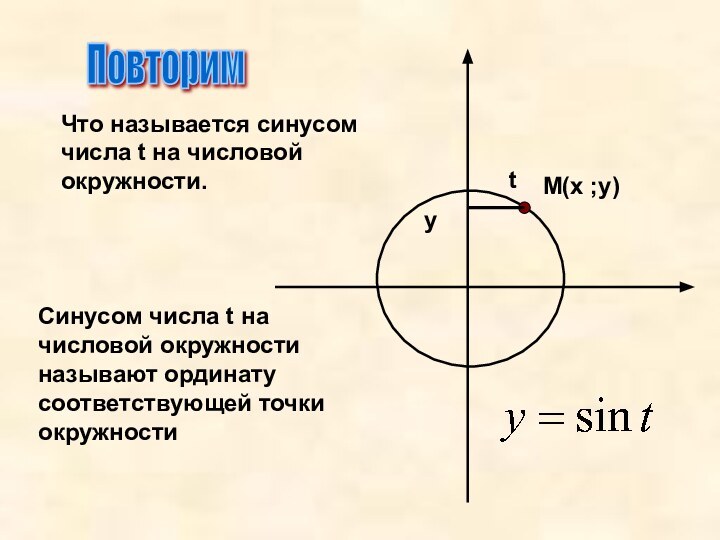
Что называется синусом числа t на числовой окружности.
Синусом
числа t на числовой окружности называют ординату соответствующей точки
окружностиМ(х ;у)
у
t
Слайд 9
С помощью числовой окружности сравним
Дуги AM и AL
равны по длине и противоположны по направлению
Слайд 20
Пример 3.
Решить неравенство
Строим окружность
Учитываем, что синус – это
ордината точки числовой окружности.
P
M
Следовательно
Данному неравенству соответствуют точки открытой дуги
MPПолучим