Слайд 2
Анализ и применение
математических
соотношений
в практической
деятельности
Цель работы:
Слайд 3
Изучить литературу по данной теме;
Рассмотреть экстремальное свойство шестиугольных
пчелиных сот;
Проверить опытным путем коэффициент полнодревесности;
Исследовать зависимость объема желоба
от угла наклона прибиваемых досок;
Показать применение формул площади и объема;
Установить зависимость площади испарения в цистерне от глубины наполнения;
Рассчитать количество краски для ремонта;
Выполнить практический расчет необходимого количества плитки для облицовки стен.
Задачи работы
Слайд 4
Методы исследования:
Моделирование;
Анализ и синтез;
Сравнение.
Слайд 5
«Странные общественные привычки и геометрические дарования пчёл
не могли не привлечь внимание и не вызвать восхищение
людей, наблюдавших плоды их деятельности».
Герман Вейль
«Далее этой ступени совершенства в архитектуре, естественный отбор не мог вести, потому что соты пчёл,- насколько мы в состоянии судить, абсолютно совершенны с точки зрения экономии труда и воска».
Чарльз Дарвин
Геометрия пчелиных сот
Слайд 6
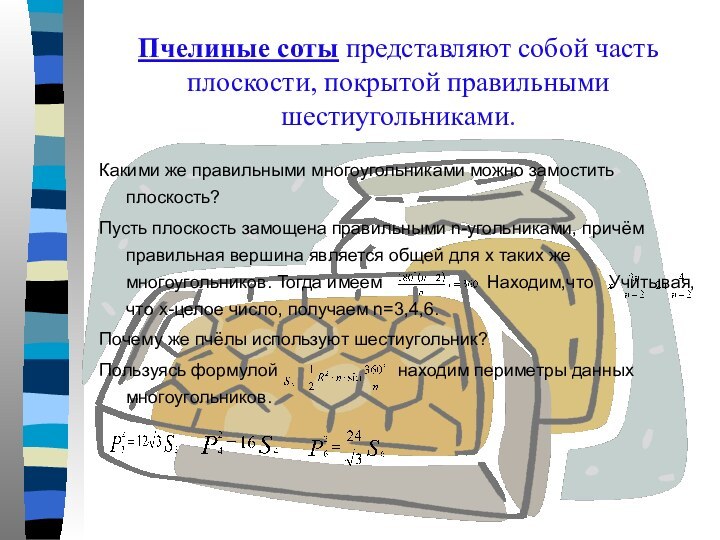
Пчелиные соты представляют собой часть плоскости, покрытой правильными
шестиугольниками.
Какими же правильными многоугольниками можно замостить плоскость?
Пусть плоскость
замощена правильными n-угольниками, причём правильная вершина является общей для x таких же многоугольников. Тогда имеем . Находим,что Учитывая, что x-целое число, получаем n=3,4,6.
Почему же пчёлы используют шестиугольник?
Пользуясь формулой находим периметры данных многоугольников.
Слайд 7
Профиль пчелиной ячейки
- правильный шестиугольник, и он из всех возможных многоугольников
с данной площадью имеет наименьший периметр, поэтому в результате эволюции сложилось так,
что пчелы используют
шестиугольник
Слайд 8
Для наиболее рационального использования леса необходимо знать
закономерности увеличения древесной массы в дереве с течением времени.
В лесоведении различают два вида прироста: средний и текущий. Текущим приростом в возрасте n лет называют величину zn=Vn-Vn-1; где Vn и Vn-1-объём дерева соответственно в возрасте n и n-1 лет. Средним приростом в возрасте n лет называют величину tn=Vn/n. При нормальных условиях средний прирост в первый период жизни возрастает(у хвойных-до 50-60 лет), а затем убывает.
Математика в лесу
Слайд 9
Коэффициент полнодревесности
штабелей
Под коэффициентом полнодревесности (Δ)
понимается отношение объёма древесины в штабеле(Vдр) к геометрическому объёму
штабеля(Vшт). Δ= Vдр/ Vшт.
Найдём Δ, считая все брёвна одинаковыми цилиндрами R=40 см.; h(Длина брёвен)=4 м.; m(количество брёвен в ряду)=4; n(количество рядов)=3.
Vдр=πR2h; Vдр=3,14•0,42•4=5,024 м.;
Vшт=mn•(2R)2•h; Vшт=4•3•4•0,42•4=30,72 м3;
Δ=12•5,024/19,2•4=0,785.
Слайд 10
Границы коэффициента полнодревесности

Поленница, которую мы рассматриваем,
представляет собой «лежащую на боку»
правильную треугольную призму.
Если в первом ряду поленницы уложено n чурок, то во втором ряду их n-1, в третьем n-2, в последнем 1. Общее количество чурок в поленнице k=n+(n-1)+…+1=n(n+1)/2. Δ=kπr2l/Sl=n(n+1) πr2/2S, где l-длина, r-радиус чурки, S-площадь поперечного сечения поленницы. Так как АВ=АD+DE+BE, а AD=BE=r•ctg30°= , DE=2(n-1)r, то АВ=2r(n-1+ ).
Следовательно, и
Значит, Δ не зависит от радиуса чурок, а зависит от количества, определяемого числом n чурок в 1-ом ряду. Пусть Δn-коэффициент полнодревесности, соответствующий данному n. Покажем, что последовательность(Δn) возрастающая. >0, откуда и вытекает, что Δn+1 > Δn.
Для возрастающей последовательности верно соотношение Δn Δ1. У нас Δ1=
= >0,60. Мы получили для Δ оценку снизу: Δ >0,60.
Для получения оценки сверху заметим, что предел a возрастающей последовательности, очевидно, больше любого члена последовательности: Δn
Слайд 11
Объём леса долготьём
1-й способ:
брёвна грузят в кузов машины, измеряют длину, ширину и
высоту кузова и находят объём кузова по формуле V=a·b·c, где a-длина, b-ширина, c-высота. Для более точного объёма умножают найденный объём на коэффициент 0,8.
2-й способ: существует множество таблиц, по которым, зная длину бревна, диаметр в верхнем и нижнем спиле можно найти объём бревна.
Слайд 12
Объём поленицы
Объём поленицы можно найти по формуле:V=a·c·h.
Задача.Найти
объём поленицы, если известно, что a=1,5,b=2,3, h=1метр.
Решение.V=1,5·2,5·1=3,75(м3).
Ответ.V=3.75 кубических метров.
Брёвна и дрова на складах лесоматериалов укладываются в штабеля
различной формы. Учёт уложенных в штабеля лесоматериалов ведётся с помощью коэффициента полнодревесности штабеля, который зависит от вида штабеля и от количества брёвен.
Слайд 14
Математика на ферме
Вычисление вместимости желоба
Задача: Водопойные желоба для
овец сбиваются из двух одинаковых досок. Под каким углом
следует сбивать доски, чтобы получить желоб наибольшего объёма?
Решение: Пусть доски имеют ширину а, и сбиты под углом α(0< α<180). Объем желоба пропорционален площади треугольника. ;поскольку sin α 1;при любом α,
то объем поилки максимален при α=90о.
Итак, для наибольшего объёма желоба доски нужно сбивать под прямым углом.
Слайд 15
Задача: Для изготовления водопойного желоба на животноводческой ферме
взяли три одинаковые доски длиной 4 метра и шириной
25 сантиметров каждая. При каком значении α получится желоб наибольшей вместимости?
Решение: Вместимость V(м3) желоба равна произведению площади трапеции (поперечное сечение) ABCD и длины желоба. Зададим формулой зависимость вместимости желоба от угла α при основании ВС трапеции ABCD и заполним таблицу:
Рассмотрим случай , когда α=100о, d=4м, а=25см,
то в поперечном сечении желоб будет иметь
форму правильной трапеции. Площадь трапеции
можно найти по формуле
, где АН-высота.
АН=ВА*cos100=25*0.9848=24.62см;
ВС= 2ВН+AD= 2(sin100)*25+25=33.6846см;
S=1/2*(33.6846+25)24.62=0.0721м2;
V=0.0721*4=0.2884м3.
Слайд 16
Остальные случаи рассматриваются аналогично. Результаты приведены в
таблице. Итак, при значении угла α=1200,получается желоб наибольшей вместимости.
Это подтвердил нам работник фермы Неупокоева Надежда Михайловна - летние поилки сбиваются именно под этим углом.
Слайд 17
Математика в поле
Площадь поля
Площадь поля находится в зависимости от его формы. Если
форма поля нестандартная (т.е. представима в виде простейших геометрических фигур), то его разбивают на простейшие геометрические фигуры, площади которых находятся уже по известным формулам.
Слайд 18
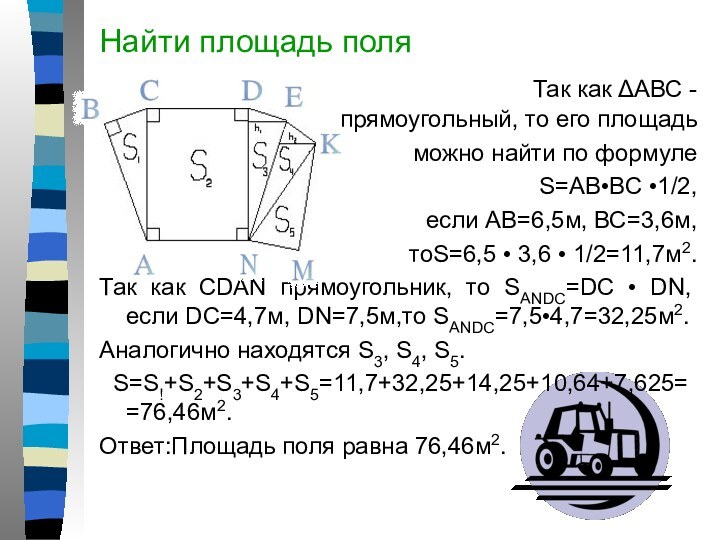
Найти площадь поля
Так как ΔАВС -прямоугольный, то его площадь
можно найти по формуле
S=AB•BC •1/2,
если АВ=6,5м, ВС=3,6м,
тоS=6,5 • 3,6 • 1/2=11,7м2.
Так как CDAN прямоугольник, то SANDC=DC • DN, если DC=4,7м, DN=7,5м,то SANDC=7,5•4,7=32,25м2.
Аналогично находятся S3, S4, S5.
S=S!+S2+S3+S4+S5=11,7+32,25+14,25+10,64+7,625= =76,46м2.
Ответ:Площадь поля равна 76,46м2.
Слайд 19
Объём стогов сена
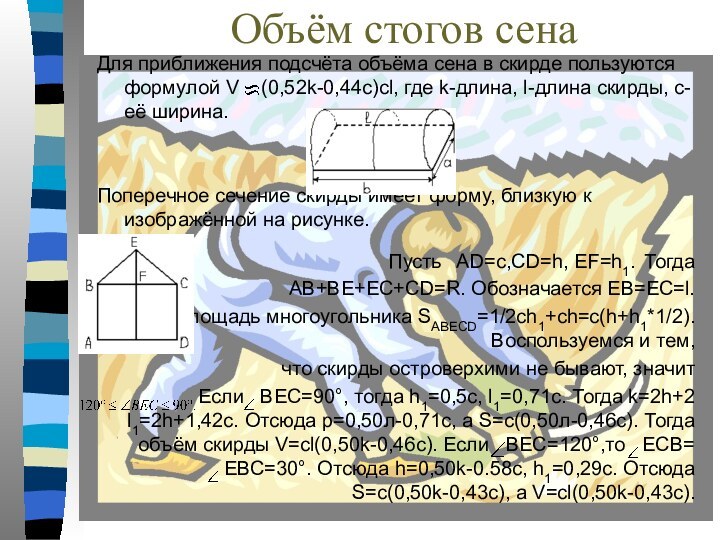
Для приближения подсчёта объёма сена
в скирде пользуются формулой V (0,52k-0,44c)cl, где k-длина,
l-длина скирды, с-её ширина.
Поперечное сечение скирды имеет форму, близкую к изображённой на рисунке.
Пусть AD=c,CD=h, EF=h1. Тогда АВ+ВЕ+ЕС+CD=R. Обозначается ЕВ=ЕС=l.
Площадь многоугольника SABECD=1/2ch1+ch=c(h+h1*1/2).Воспользуемся и тем,
что скирды островерхими не бывают, значит
Если ВЕС=90°, тогда h1=0,5с, l1=0,71с. Тогда k=2h+2 l1=2h+1,42c. Отсюда р=0,50л-0,71с, а S=c(0,50л-0,46с). Тогда объём скирды V=cl(0,50k-0,46c). Если ВEC=120°,то ЕСВ= ЕВС=30°. Отсюда h=0,50k-0.58c, h1=0,29c. Отсюда S=c(0,50k-0,43c), а V=cl(0,50k-0,43c).
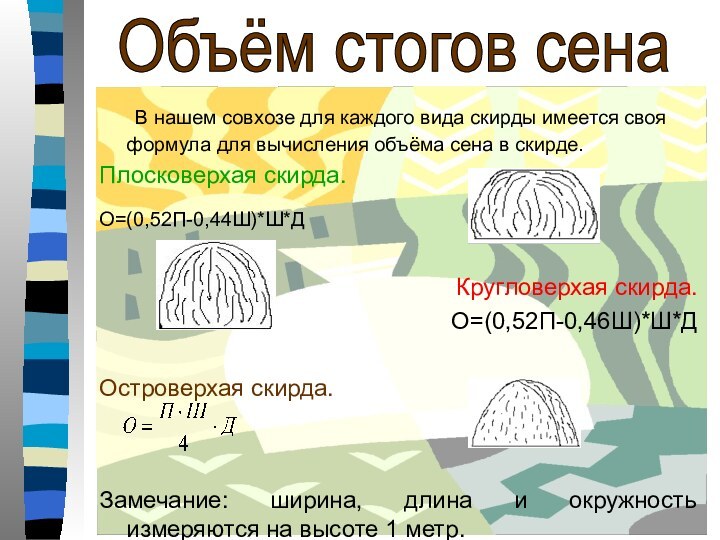
Слайд 20
В нашем совхозе для каждого
вида скирды имеется своя формула для вычисления объёма сена
в скирде.
Плосковерхая скирда.
О=(0,52П-0,44Ш)*Ш*Д
Кругловерхая скирда.
О=(0,52П-0,46Ш)*Ш*Д
Островерхая скирда.
Замечание: ширина, длина и окружность измеряются на высоте 1 метр.
Объём стогов сена
Слайд 22
Математика на заправочной станции.
Слайд 23
Задача. Выясним, насколько эмпирическая формула для вычисления площади

поверхности испарения горючего в резервуарах цилиндрической формы, расположенных горизонтально,
удовлетворяет потребностям практики.
Решение. Выясним насколько целесообразно применять эту формулу на практике.
Пусть длина цистерны AD= l. Тогда следует, что S=AB·l.
Если пользоваться данной формулой, то
Такое соотношение выполняется при или
а это имеет место при или . При , а
следовательно, и . При
Глубину слоя горючего, наполняющего резервуар, принято называть стрелкой.
Таким образом,данная формула выведена в расчёте,что стрелка или
Совершенно очевидно, что такой уровень горючего в резервуаре может оказаться лишь в отдельных случаях. Выясним, насколько существенно отличается площадь испарения от указанной в формуле при значениях стрелки, отличных от указанных выше.
Произведенное исследование позволяет сделать вывод, что при формула приемлема. При и , и по мере удаления значений стрелки КМ от d/4 и 3d/4 отклонения действительной площади испарения от площади, указанной в данной формуле, быстро растут и становятся весьма значительными.
Слайд 24
Для определения количества жидкости в
цистерне, размеры которой: диаметр d=200см, длина l=500см, достаточно измерить
высоту столба жидкости «h» и воспользоваться графиком.
Задача. Найдём, используя график: сколько литров жидкости в цистерне, если высота столба жидкости равна:
а)15 см; б) 25 см.
Решение. Воспользуемся графиком
0 20 40 60 80 100 120 140 160 180 200 220 h,см
Ответ: а)V=10гл, б)V=18гл.
Слайд 25
Прикладная математика дома
Задача: сколько потребуется килограммов краски для
покраски пола кабинета?
Решение: так как пол кабинета математики имеет
форму прямоугольника, то его площадь можно найти по формуле S=a*b, где а - длина, b - ширина. Измерив длину и ширину пола, получаем а=8,55м, b=6,1м. Sк=52,155м2.
На этикетке каждой банки краски написано, сколько краски требуется на квадратный метр. Средний расход краски равен 200г на 1м2.
Если количество нужной краски обозначить за К, то
К= Sк*расход краски.
К=52,155*0,2=10,431кг.
Ответ: для покраски пола потребуется 10,431 килограммов краски.
Слайд 26
Задача.
Пол комнаты, имеющий прямоугольную форму со сторонами
5,5 и 6м, нужно покрыть паркетом прямоугольной формы. Длина
каждой дощечки паркета 30см, ширина 5 см. Сколько потребуется таких дощечек для покрытия всего пола?
Решение.
Так как форма пола - прямоугольник, то его площадь можно найти по формуле S=a*b. Sпола=5,5*6=33м2=33000см2;
так как форма дощечки паркета прямоугольная то её площадь можно найти по формуле S=a*b. Sдощечки=30см*5см=150см2;
Обозначим количество дощечек за К. К= Sпола/ Sдощечки
К = 33000см2/150см2=2200
Ответ.
Для покрытия пола паркетом нужно 2200 паркетных дощечек.
Слайд 27
Задача.
Сколько потребуется кафельных плиток квадратной формы со
стороной 15 см, для облицовки части стены, если длина
стены 3 метра, высота 2,7 метра.
Решение.
Найдем площадь плитки: так как плитка имеет форму квадрата, то её площадь равна S=a2. Sплитки = 152 = 225см2=0,0225м2. Так как стена имеет форму прямоугольника, то её площадь равна S=a*b, Sстены=3*2,7=8,1м2.
Обозначим количество плиток за К.
К= Sстены/ Sплитки
К= 8,1м2/0,0225м2=360.
Ответ.
Для облицовки стены потребуется 360 плиток