tg
k = ctg
- угол между прямой и
осью Охy= kx+b
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть








![Применение производной к исследованию функций Непрерывная функция у = f(x) задана на отрезке [a; b].](/img/tmb/12/1109229/1024baaf75447584aafc2f47521eb744-720x.jpg)
![Применение производной к исследованию функций Непрерывная функция у = f(x) задана на отрезке [a; b].](/img/tmb/12/1109229/e90b41445a95e559b3bb2c5795da00ee-720x.jpg)






![Применение производной к исследованию функций Непрерывная функция у = f(x) задана на отрезке [a;b]. На](/img/tmb/12/1109229/9e0c0755d1df7e7f3b83307831412736-720x.jpg)


y= kx+b
нулю.
f ' (х)= k= tg
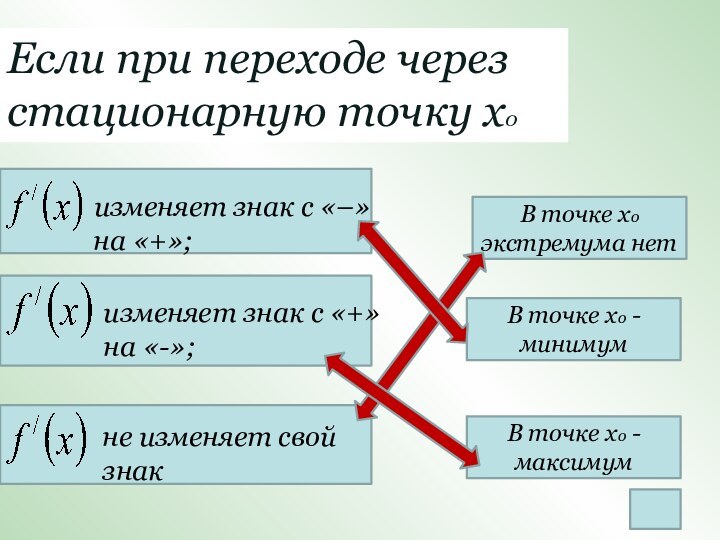
не изменяет свой знак
В точке хо экстремума нет
В точке хо - минимум
В точке хо - максимум
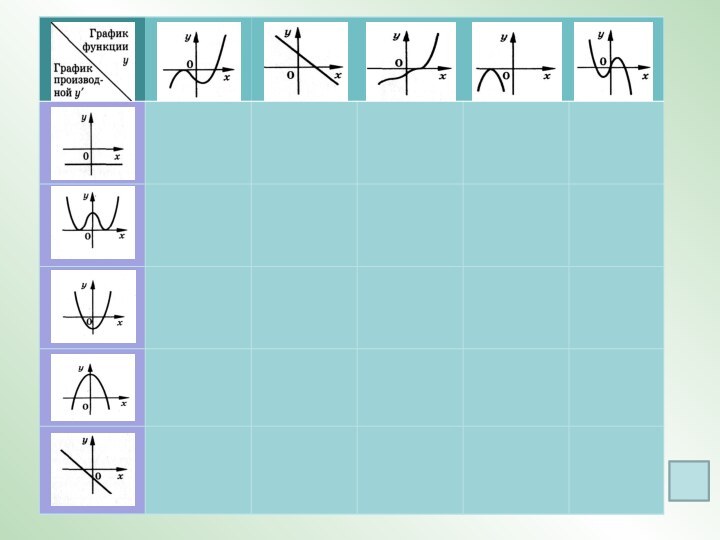
y = f(x)
y
x
a
b
y = f/(x)
y
x
a
b
Функция у = f(x) определена на промежутке (- 4; 3). На рисунке изображен график ее производной. В какой точке отрезка [-3;0]
у = f(x) принимает наибольшее значение?
y = f /(x)
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
y
x
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
y
x
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
7
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
7
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
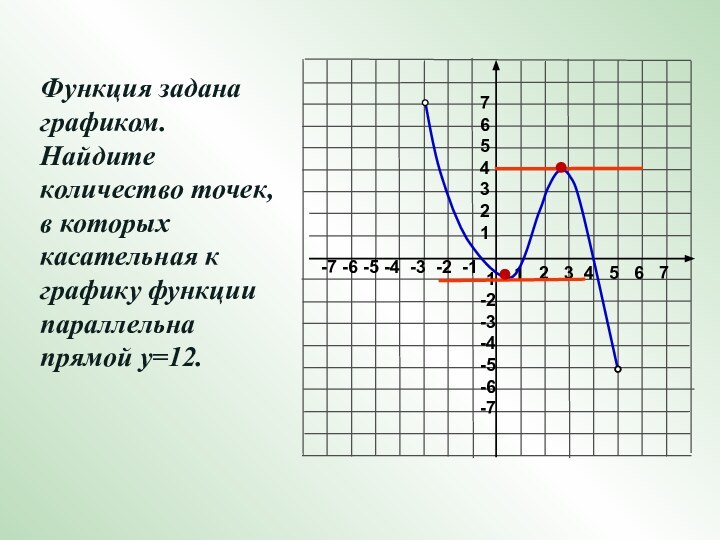
Функция задана графиком. Найдите количество точек, в которых касательная к графику функции параллельна прямой у=12.
y = f(x)
y
x
a
b
х0
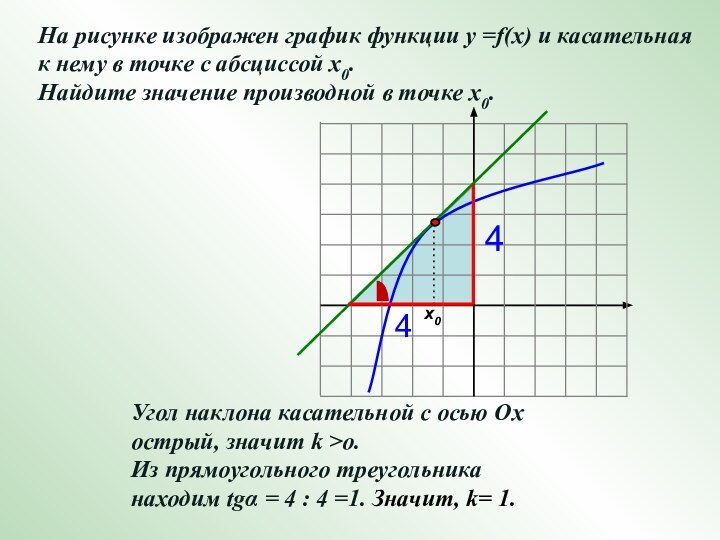
Угол наклона касательной с осью Ох острый, значит k >o.
Из прямоугольного треугольника
находим tgα = 4 : 4 =1. Значит, k= 1.
4
4
На рисунке изображен график функции у =f(x) и касательная
к нему в точке с абсциссой х0.
Найдите значение производной в точке х0.
х0
6
3
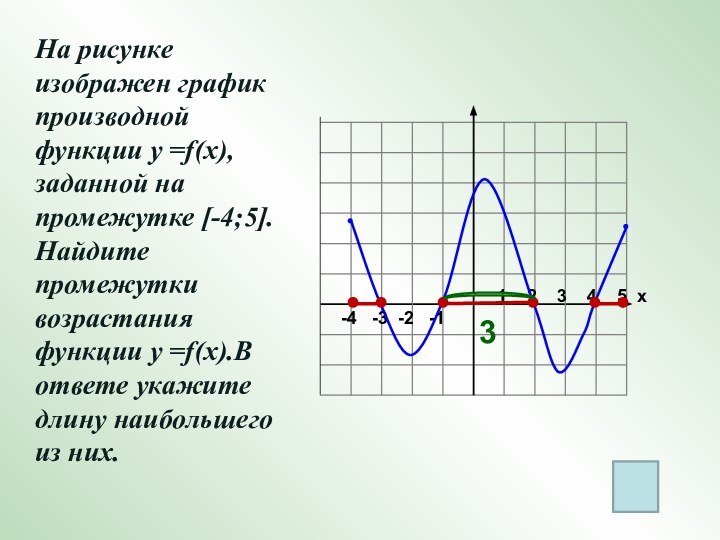
На рисунке изображен график производной функции у =f(x),
заданной на промежутке [-4;5]. Найдите промежутки возрастания функции у =f(x).В ответе укажите длину наибольшего из них.
3