- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему В мире треугольников
Содержание
- 2. Цель работы:Узнать о треугольнике за страницами школьного учебника;Показать применение треугольников в окружающей жизни.
- 4. Треугольник ПаскаляАрифметический
- 5. Пифагоров треугольникПифагоровыми треугольниками называются прямоугольные треугольники,
- 7. Виды треугольниковТреугольник называется равнобедренным,
- 8. БиссектрисаБиссектриса угла — это
- 11. Серединный перпендикулярПрямую, проходящую через середину отрезка перпендикулярно
- 12. Средняя линияСредней линией треугольника называется
- 14. Бермудский Треугольник (продолжение)Правда это или вымысел журналистов
- 19. Отгадай ребусыОтвет : ТреугольникУ
- 21. Словарик - памяткаТригонометрия-раздел геометрии, в котором
- 23. Скачать презентацию
- 24. Похожие презентации
Цель работы:Узнать о треугольнике за страницами школьного учебника;Показать применение треугольников в окружающей жизни.





















Слайд 2
Цель работы:
Узнать о треугольнике за страницами школьного учебника;
Показать
применение треугольников в окружающей жизни.
Слайд 3
Историческая справка.
Математики треугольник называют двумерным симплексом.<<Симплекс>> по-латыни означает простейший. Трёхмерным симплексом называют треугольную пирамиду. Именно в силу своей простоты треугольник явился основой многих измерений. Землемеры при вычислениях площадей земельных участков и астрономы при нахождении расстояний до данного объекта используют свойства треугольников. Так возникла наука тригонометрия-наука об измерении треугольников о выражении сторон через углы.
Через площадь треугольника выражается площадь любого многоугольника: достаточно разбить этот многоугольник на треугольники, вычислить их площади и сложить результаты. Правда, верную формулу для площади треугольника удалось найти не сразу. В одном египетском папирусе 4000-летней давности говорится , что площадь равнобедренного треугольника равна произведению ½ основания на боковую сторону , а не на высоту.
Через 2000 лет в Древней Греции изучение свойств треугольника ведётся очень активно . Пифагор открывает свою теорему. Герон находит формулу , выражающую площадь треугольника через его стороны ; становится известным , что биссектрисы, как медианы и высоты, пересекаются в одной точке.
Особенно активно свойства треугольника исследовались в XV__XVI веках . Вот одна из теорем того времени, принадлежащая Леонарду Эйлеру : « Середины сторон треугольника, основания его высот и середины отрезков высот от вершины до точки их пересечения лежат на одной окружности»
Наполеон иногда свободное время посвящал занятиям математикой. Ему приписывают такую красивую теорему: если на сторонах треугольника во внешнюю сторону построить равносторонние треугольники, то их центры будут вершинами равностороннего треугольника.
Слайд 4
Треугольник Паскаля
Арифметический треугольник-таблица
чисел, являющихся биномиальными коэффициентами .
1_______________________2ª,а=01___1_____________________2¹
1__2__1____________________2²
1__3__3__1__________________2³
1__4__6__4 __1________________2ª,а=4
1__5 __10__10__5__1_____________2ª, а=5
1__6__15__20__15__6__1___________2ª, а=6
Слайд 5
Пифагоров треугольник
Пифагоровыми треугольниками называются прямоугольные треугольники, длины
сторон которых выражаются целыми числами.
Например треугольники со сторонами
1) 3,4,5 ; 2)5,12,13 ; 3)17,8,15. 3
12
15
5
4
13
5
17
8
Слайд 6 Египетский
треугольник
Треугольник со сторонами 3,4,5-назывался египетским треугольником, он был известен
ещё в древними египтянами служил для построение прямых углов на местности . В вавилонских текстах эта теорема встречается за 1200 лет до Пифагора . Возможно , что тогда ещё не знали её доказательства , а само соотношение между гипотенузой и катетами было установлено опытным путём на основе измерений .
Слайд 7
Виды треугольников
Треугольник называется равнобедренным, если
у него две стороны равны. Эти равные стороны называются
боковыми сторонами, а третья сторона называется основанием треугольника.Треугольник, у которого все стороны равны, называется равносторонним или правильным.
Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой, две другие стороны называются катетами.
Треугольник называется остроугольным, если все три его угла — острые, то есть меньше 90°.
Треугольник называется тупоугольным, если один из его углов — тупой, то есть больше 90°.
Слайд 8
Биссектриса
Биссектриса угла — это луч,
который исходит из его вершины, проходит между его сторонами
и делит данный угол пополам. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.Свойства биссектрис треугольника
Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла.
Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилегажащим сторонам: .
Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник.
Слайд 9
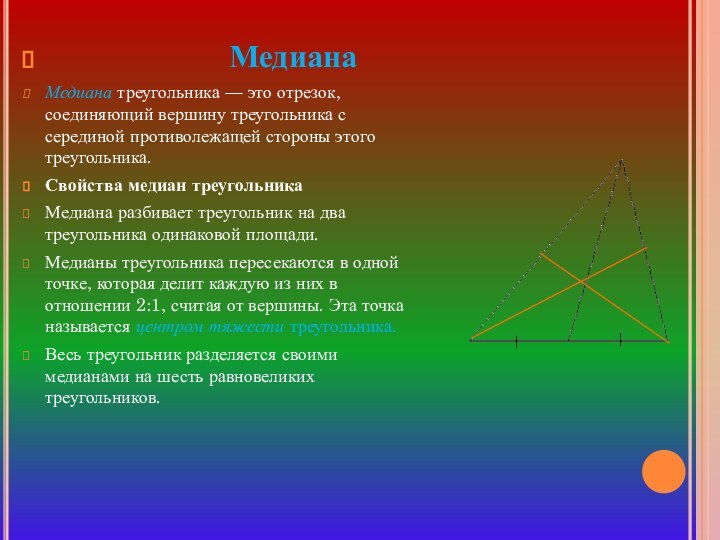
Медиана
Медиана треугольника — это отрезок, соединяющий вершину
треугольника с серединой противолежащей стороны этого треугольника.Свойства медиан треугольника
Медиана разбивает треугольник на два треугольника одинаковой площади.
Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.
Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.
Слайд 10
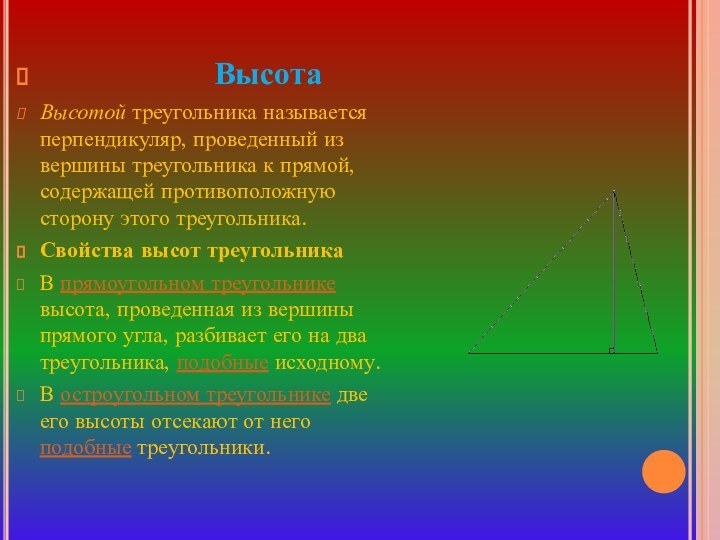
Высота
Высотой треугольника называется перпендикуляр, проведенный из вершины
треугольника к прямой, содержащей противоположную сторону этого треугольника.Свойства высот треугольника
В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному.
В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.
Слайд 11
Серединный перпендикуляр
Прямую, проходящую через середину отрезка перпендикулярно к
нему, называют серединным перпендикуляром к отрезку.
Свойства серединных перпендикуляров треугольника
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника
Слайд 12
Средняя линия
Средней линией треугольника называется отрезок,
соединяющий середины двух его сторон.
Свойство средней линии треугольника
Средняя линия
треугольника параллельна одной из его сторон и равна половине этой стороны.А
В
Слайд 13 Бермудский
Треугольник
Треугольник. С одной стороны – это простая геометрическая фигура.
С другой стороны – тайный оккультный знак, встречающийся во многих цивилизациях. Три угла, три грани…магическое число 3. Немудрено, что треугольник можно найти на тайных письменах, символах, пентаграммах. И совсем не удивительно, что самые загадочные места и строения могут быть связаны тоже с треугольниками: египетские пирамиды, звезда Давида (еврейский символ, образованный наложением двух треугольников), Бермудский треугольник.
Первое упоминание о Бермудском треугольнике можно отнести к середине 20 века. До этого времени это было ничем не выдающееся место. Считается, что первые мистические случаи стали происходить возле самих Бермудских островов, что и послужило окончательным названием всей территории. С тех пор писатели и журналисты не давали этой месту покоя, прославив его на века.
Бермудский треугольник не имеет четких границ, нельзя найти на карте его точное обозначение. Разные ученые определяют его местоположение на свое усмотрение. Самое распространенное его определение – это область в Атлантическом океане между Бермудами, Пуэрто-Рико и Майами. Общая площадь – 1 млн. квадратных километров. Однако название этой области тоже условное, поэтому название «Бермудский треугольник» не является географическим.
Бермудский треугольник имеет дурную славу. Существует огромное число свидетельств исчезновения в нем кораблей, самолетов, подводных лодок. Более того, если судно все-таки удавалось найти, то экипаж и пассажиры пропадали бесследно. Следов поломок или сигнала бедствия ни в одном случае не было. Были также свидетельства исчезновения объектов с радаров на несколько минут.
Слайд 14
Бермудский Треугольник (продолжение)
Правда это или вымысел журналистов –
разобраться трудно. Скорее всего, реальные истории переплетаются с легендами,
обрастают слухами. Сбивает с толку еще и то, что снято слишком много фильмов и написано много книг про этот феномен. Поэтому отделить реальность от домыслов тяжелее вдвойне. Остается собирать факты по крупицам. Можно сказать с достоверностью, что ландшафт дна, направление ветров и течения в этом месте достойны изучения. При определенных стечениях обстоятельств здесь могут встречаться и аномалии. Давно доказано, что эта зона подвержена частому появлению торнадо, сильных штормов, что уже небезопасно для судов, а волнения в атмосфере могут подстерегать самолеты в воздухе. Существует много публикаций о том, что пассажирские и торговые рейсы стараются пустить в обход Бермудского треугольника. Однако это далеко от реальности, т.к. слишком дорого делать такой крюк. Да и люди, побывавшие в треугольнике, свидетельствуют, в основном, что никакой чертовщины не наблюдали. Сверхъестественные ощущения пассажиров можно приписать мнительности, а сбой техники – усилению магнитных полей или шторму. В настоящее время побережья, граничащие с территорией Бермудского треугольника, весьма популярны среди туристов. Прекрасные пляжи, чудесная природа и экзотика притягивает. Многих привлекает «дурная» слава, одного из самых загадочных мест планеты. Ведь лучше проверить все на собственном опыте. Дерзайте и не отчаивайтесь, если не найдете того, чего ожидаете, ведь легенды о Бермудском треугольнике могут оказаться одной из великих мистификаций нашего времени.Слайд 18
Дорожные знаки
Треугольники встречаться на дорогах – это дорожные
знаки, которые называются Предупреждающие знаки"
Слайд 21
Словарик - памятка
Тригонометрия-раздел геометрии, в котором изучают
тригонометрические функции и их свойства.
Треугольник-многоугольник с тремя сторонами и
тремя вершинами; фигура, образованная тремя точками, не лежащих на одной прямой, и тремя соединяющими их отрезками.Медиана- отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса-отрезок, биссектрисы угла треугольника, соединяющий вершину треугольника с точкой пересечения.
Средняя линия- отрезок, соединяющий середины двух его сторон.
Серединный перпендикуляр- перпендикуляр, восстановленный в середине стороны треугольника.
Слайд 22
Вывод:
Треугольник – геометрическая фигура, которая часто используется
для вычисления площади любого участка неправильной формы.Теоремы треугольников используются при решении задач, а эти расчёты могут быть использованы при строительстве, разметке участка, составление чертежа.
Треугольник – оптимальная форма, к которой стремится любой природный объект, например ,
горная вершина.
Треугольная крыша наиболее удобная при строительстве зданий, так как на ней не остаётся осадков.





























