практическое применение.
Задачи:
• изучить виды симметрии, преобразования;
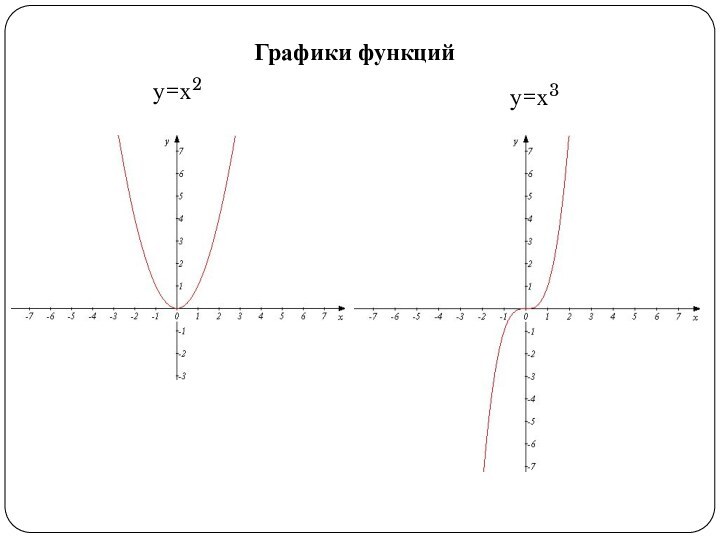
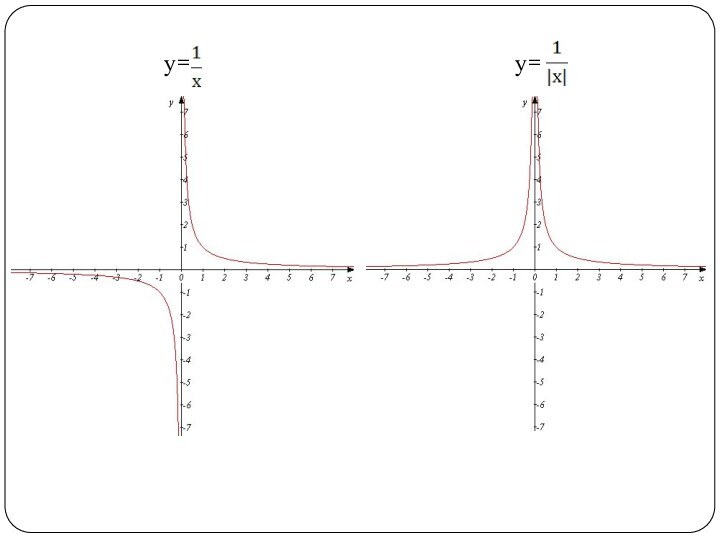
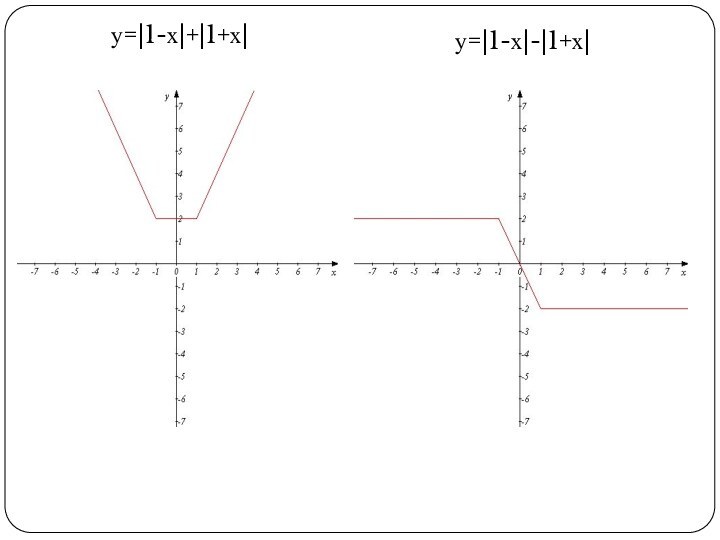
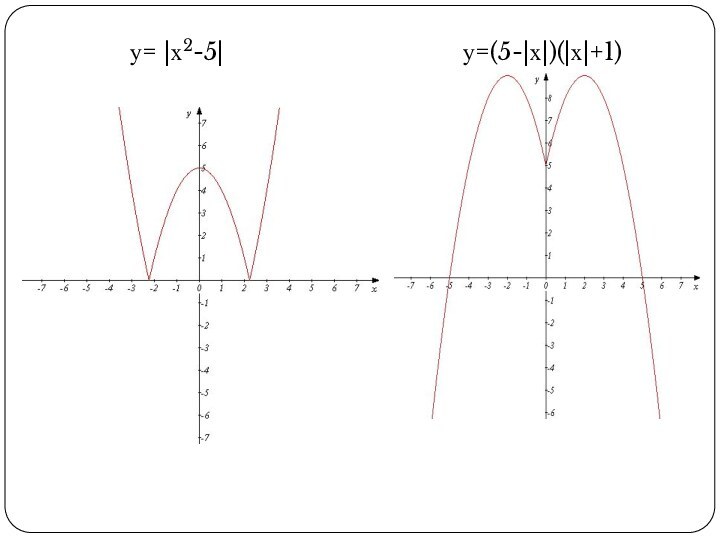
• изучить понятие
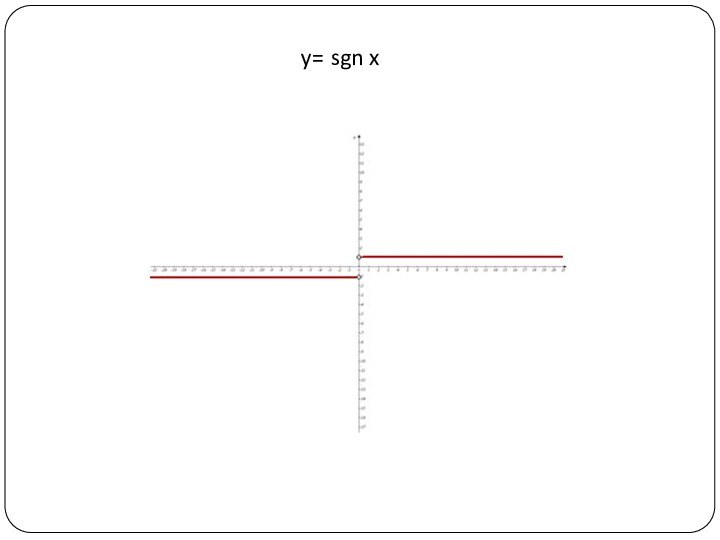
«функция», способы задания функции, свойства функции;• изучить методы решения уравнений высших степеней;
• показать практическое применение данных вопросов.