- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Проект по теме Сколько средних линий в трапеции?
Содержание
- 2. «Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли…» В.Произволов
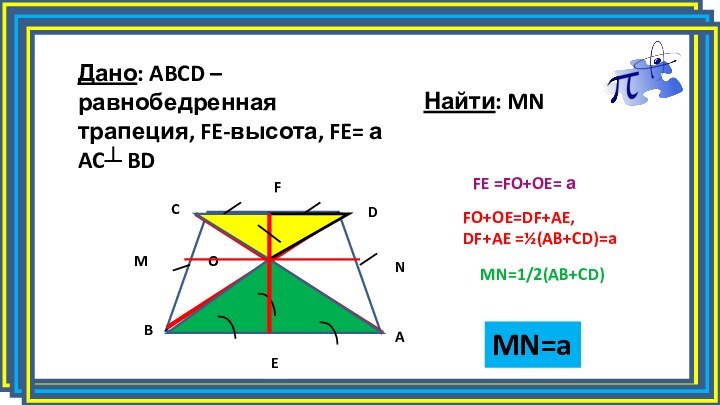
- 3. FE =FO+OE= аFO+OE=DF+AE, DF+AE =½(AB+CD)=aДано: ABCD –равнобедренная трапеция, FE-высота, FE= а AC┴ BDНайти: MNMN=1/2(AB+CD)MN=a
- 4. «А есть ли еще средние линии в трапеции?»
- 5. Задачи исследования:подобрать данные о средних линиях трапецииизучить
- 6. Актуальность, новизна и практическая значимость:Наше исследование актуально
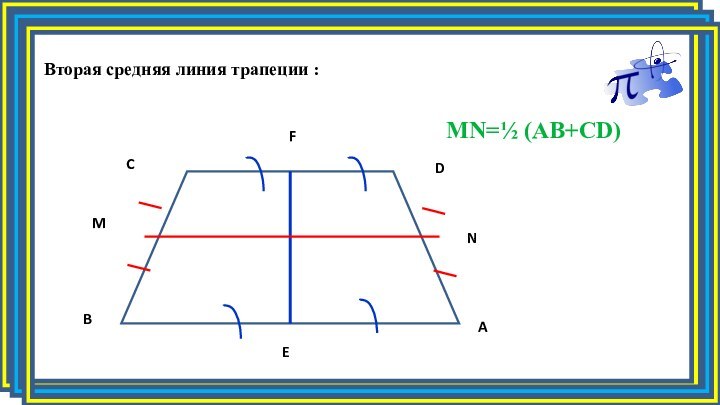
- 7. Вторая средняя линия трапеции :MN=½ (AB+CD)
- 8. B1A1
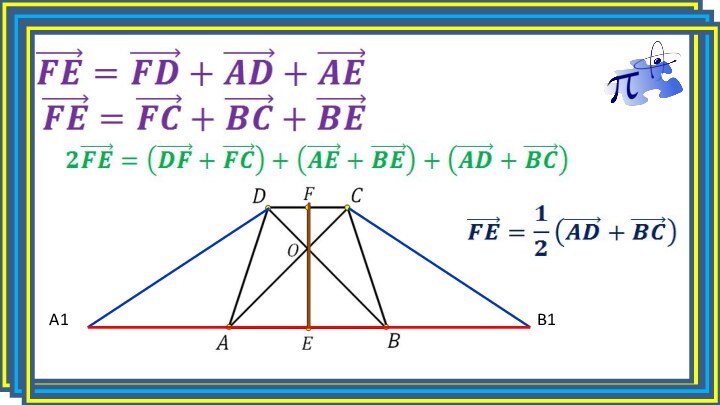
- 9. В точке, в которой пересекаются две средние
- 10. Дано: ВК=КСДоказать: AS=SDAS=SDДиагонали трапеции и вторая средняя линия пересекаются в одной точке~ ~BK=KC
- 11. OCDBASKOK=½ (ОВ+ОС), OS=½ (OA+OD), OS=½ (k∙OB +
- 12. AC BDСредние линии равнобедренной трапеции
- 13. Задача 1. (Кушнир И. А.) В трапеции
- 14. Задача 2 (Кушнир И.А.)Доказать, что площадь трапеции
- 15. Задача 3. (Кушнир И. А.)В трапеции ABCD
- 16. Задача 1 (составлена самостоятельно)Верно ли утверждение: если
- 17. Задача 2 (составлена самостоятельно)В трапеции ABCD вторая
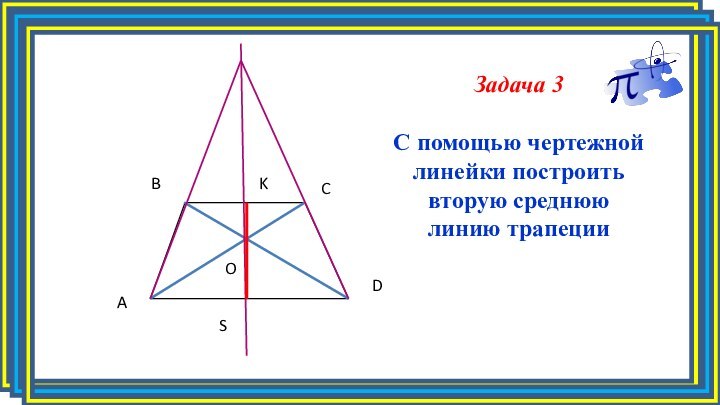
- 18. CDAOBSKЗадача 3С помощью чертежной линейки построить вторую среднюю линию трапеции
- 19. Задача 4Найдите среднюю линию трапеции АВСD, если
- 20. Задача 5 Вторая средняя линяя равнобокой
- 21. ВЫВОДЫ:1. В процессе собственных информационных поисков получены
- 22. Скачать презентацию
- 23. Похожие презентации









Слайд 3
FE =FO+OE= а
FO+OE=DF+AE,
DF+AE =½(AB+CD)=a
Дано: ABCD –равнобедренная
трапеция, FE-высота, FE= а AC┴ BD
Найти: MN
MN=1/2(AB+CD)
MN=a
Слайд 5
Задачи исследования:
подобрать данные о средних линиях трапеции
изучить особенные
особенности средних линий в трапеции
исследовать задачи о средних линиях
трапеции, действующие в математической литературеразобрать конкретные вопросы о средних линиях трапеции
Цель исследования:
установить, сколько средних линий имеет трапеция
Обьект исследования: трапеция
Предмет исследования: средние линии трапеции
Слайд 6
Актуальность, новизна и практическая значимость:
Наше исследование актуально и
ново, поскольку в школьной программе по математике данное направление
не рассматривалось более глубоко и основательно.В процессе собственных информационных поисков получены не известные факты для школьников о второй средней линии трапеции.
Данные исследования будут полезны при подготовке к математическим олимпиадам и конкурсам, более углубленного изучения геометрии, а также поможет обычным школьникам стать более успешными в математике, поскольку данная тема является важной при подготовке к ОГЭ.
Гипотеза: Если знать в совершенстве основные особенности средних линий трапеции, то их применение будет хорошим подспорьем ученикам в практическом направлении материала
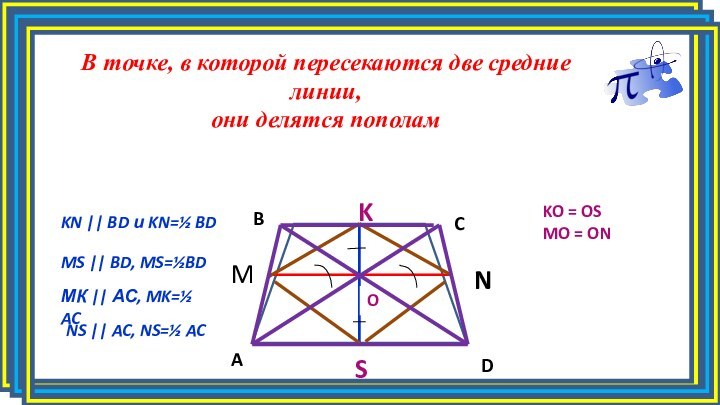
Слайд 9 В точке, в которой пересекаются две средние линии,
они делятся пополам
KO = OS
MO = ON
KN || BD
и KN=½ BDMS || BD, MS=½BD
МК || АС, MK=½ AC
NS || AC, NS=½ AC
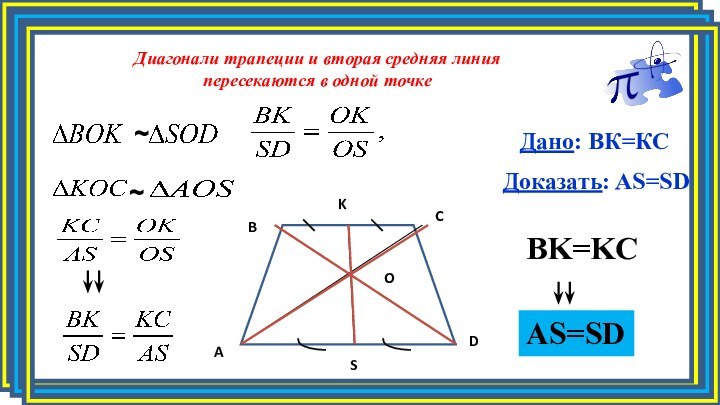
Слайд 10
Дано: ВК=КС
Доказать: AS=SD
AS=SD
Диагонали трапеции и вторая средняя линия
пересекаются в одной точке
~
~
BK=KC
Слайд 11
O
C
D
B
A
S
K
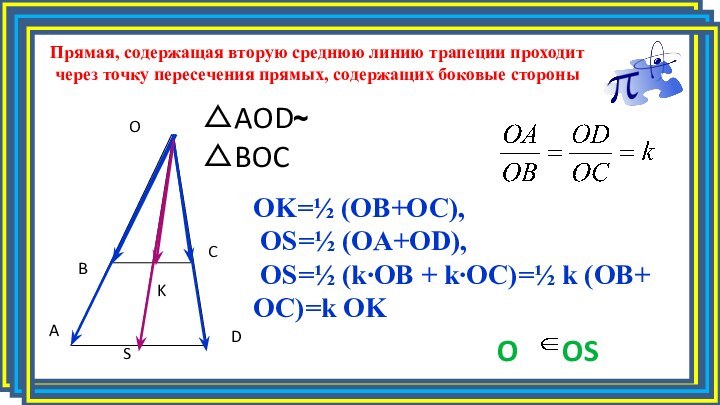
OK=½ (ОВ+ОС),
OS=½ (OA+OD),
OS=½ (k∙OB + k∙OC)=½
k (OB+ OC)=k OK
△AOD △BOC
Прямая, содержащая вторую
среднюю линию трапеции проходит через точку пересечения прямых, содержащих боковые стороны~
O OS
Слайд 12
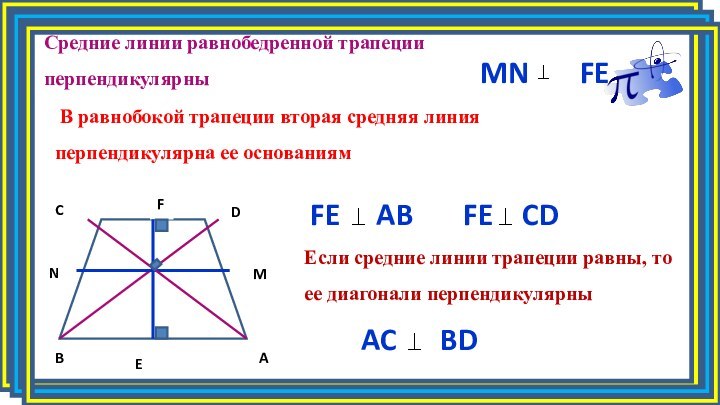
AC BD
Средние линии равнобедренной трапеции перпендикулярны
MN
FE
В равнобокой трапеции вторая средняя
линия перпендикулярна ее основаниямFE AB
FE CD
Если средние линии трапеции равны, то ее диагонали перпендикулярны
Слайд 13
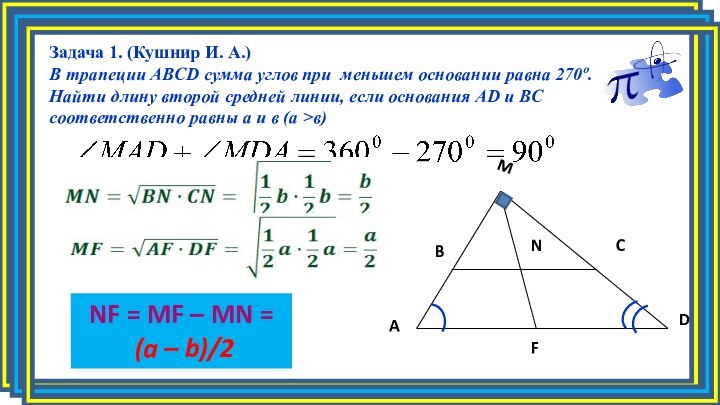
Задача 1. (Кушнир И. А.)
В трапеции ABCD
сумма углов при меньшем основании равна 270º. Найти длину
второй средней линии, если основания AD и BC соответственно равны а и в (а >в)C
D
A
N
B
F
M
NF = MF – MN =
(a – b)/2
Слайд 14
Задача 2 (Кушнир И.А.)
Доказать, что площадь трапеции равна
произведению второй средней линии на сумму перпендикуляров, проведенных к
этой средней линии (или её продолжению) из двух противоположных вершин трапецииC
D
F
E
B
A
N
M
Дано: ABCD – трапеция, EF – вторая средняя линия, СN EF, AM EF.
Доказать:
Доказательство: Рассмотрим △ AEF и△ ECF
Слайд 15
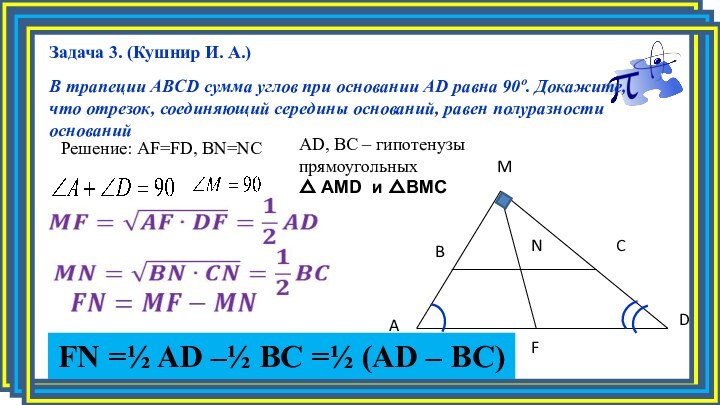
Задача 3. (Кушнир И. А.)
В трапеции ABCD сумма
углов при основании AD равна 90º. Докажите, что отрезок,
соединяющий середины оснований, равен полуразности основанийC
D
A
N
B
F
M
Решение: AF=FD, BN=NC
AD, BC – гипотенузы прямоугольных
△ AMD и △BMC
FN =½ AD –½ BC =½ (AD – BC)
Слайд 16
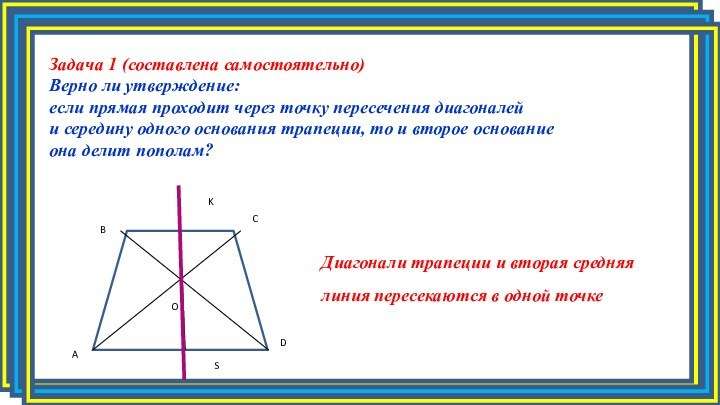
Задача 1 (составлена самостоятельно)
Верно ли утверждение:
если прямая
проходит через точку пересечения диагоналей
и середину одного основания
трапеции, то и второе основание она делит пополам?
Диагонали трапеции и вторая средняя линия пересекаются в одной точке
Слайд 17
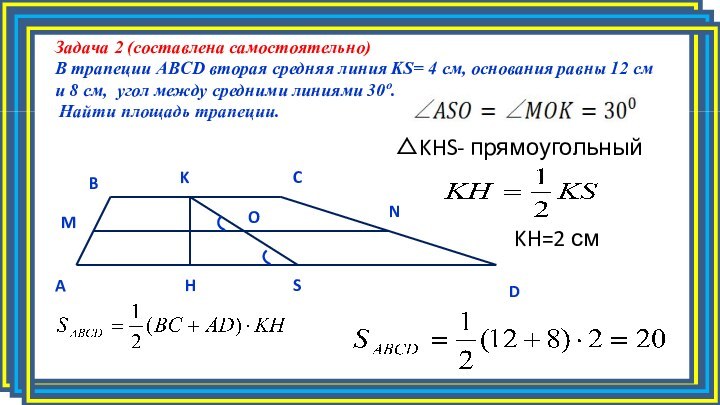
Задача 2 (составлена самостоятельно)
В трапеции ABCD вторая средняя
линия KS= 4 см, основания равны 12 см и
8 см, угол между средними линиями 30º.Найти площадь трапеции.
M
B
N
K
O
C
D
S
H
A
KH=2 см
△KHS- прямоугольный
Слайд 19
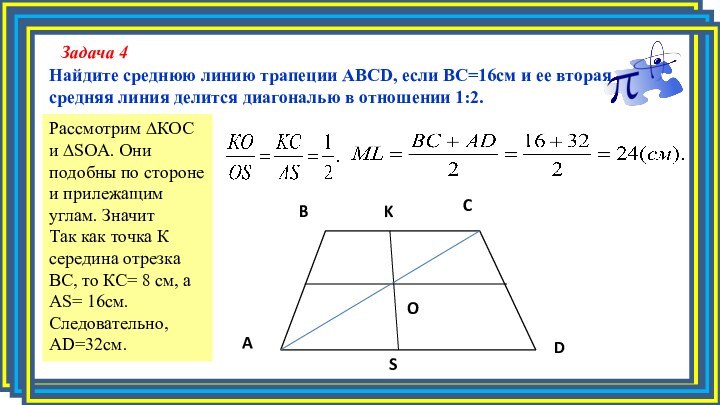
Задача 4
Найдите среднюю линию трапеции АВСD, если ВС=16см
и ее вторая средняя линия делится диагональю в отношении
1:2.C
D
A
O
B
S
K
Рассмотрим ∆КОС и ∆SOA. Они подобны по стороне и прилежащим углам. Значит Так как точка К середина отрезка ВС, то КС= 8 см, а АS= 16cм. Следовательно, AD=32cм.
Слайд 20 Задача 5 Вторая средняя линяя равнобокой трапеции перпендикулярна
её основаниям.
△АОD и △ВОС равнобедренные
ОМ и ОК медианы
M
KM┴BC, KM┴AD
Слайд 21
ВЫВОДЫ:
1. В процессе собственных информационных поисков получены не
известные факты для школьников о второй средней линии трапеции.
2.
Изучены особенные свойства средней линии3. Рассмотрены практическое решение
математических задач с использованием свойств средней линии трапеции.
4. Составлены собственные математические задачи и их решение.
5. Получены новые для меня знания и умения, повысилась заинтересованность к изучению математики.