- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Свойства случайных погрешностей
Содержание
- 2. Свойства случайных погрешностей
- 3. Вероятнейшие ошибки
- 4. Вероятнейшие ошибки
- 5. Средняя квадратичная ошибка отдельного измерения
- 6. Средняя квадратичная ошибка отдельного измерения
- 7. Кривая Гаусса
- 8. Кривая Гауссас1>сДля с1 кривая получается более узкая, чем для c. Такой ряд будет более точный.
- 9. Кривая Гаусса
- 10. Средняя среднеквадратичная ошибка окончательного результата измерений
- 11. Предельная случайная ошибкаПредельной случайной ошибкой xпр называют
- 12. Предельная случайная ошибка
- 13. Доверительный интервалПредыдущая запись справедлива при достаточно большом
- 14. Доверительный интервал
- 15. Практическое занятие №1Задание 2. Найти среднюю квадратичную
- 16. Практическое занятие №1
- 17. Практическое занятие №1
- 18. Практическое занятие №1Задание 2. Повторить вычисления пунктов
- 19. Скачать презентацию
- 20. Похожие презентации
Свойства случайных погрешностей


















Слайд 8
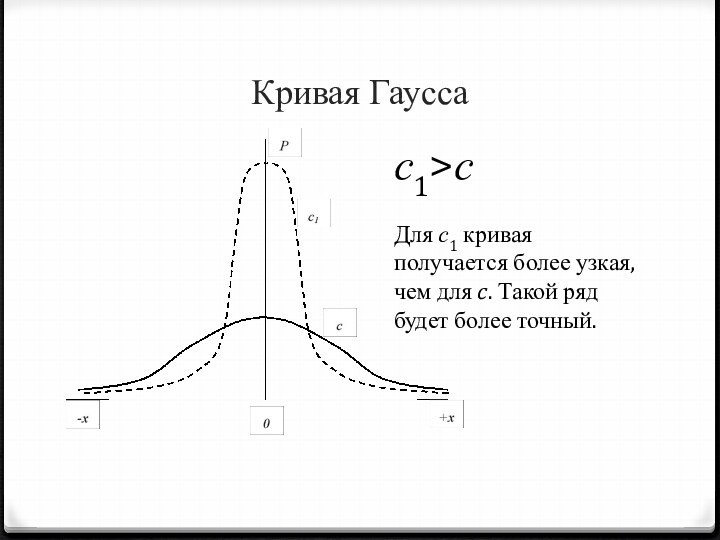
Кривая Гаусса
с1>с
Для с1 кривая получается более узкая, чем
для c. Такой ряд будет более точный.
Слайд 11
Предельная случайная ошибка
Предельной случайной ошибкой xпр называют самую
большую из всех случайных ошибок в данном ряду равноточных
измерений.Случайные ошибки распределяются по отношению к средней квадратичной ошибке отдельного измерения следующим образом:
68,3 % случайных ошибок меньше Sn;
95,7 % этих ошибок меньше 2Sn;
99,7 % − меньше 3Sn.
Таким образом, принимают, что для всякого рода равноточных измерений предельная случайная ошибка с вероятностью, близкой к 100 %, равна 3Sn
Слайд 13
Доверительный интервал
Предыдущая запись справедлива при достаточно большом числе
измерений.
В 1908 году Уильям Сили Госсет (псевдоним Стьюдент),
применил статистический подход при определении ошибок для небольшого числа измерений (менее 30). При этом в случае n → ∞, распределение Стьюдента переходит в распределение Гаусса.Если существует величина α вероятности отличия результата измерений от истинного значения на величину не более, чем Δaсл, она называется доверительной вероятностью, а интервал значений oт X−Δaсл до X+Δaсл называется доверительным интервалом.
Слайд 15
Практическое занятие №1
Задание 2.
Найти среднюю квадратичную ошибку
отдельного измерения Sn и среднюю среднеквадратичную ошибку S результатов
50-ти измерений маятника №1 по зависимостям
Слайд 18
Практическое занятие №1
Задание 2.
Повторить вычисления пунктов 1-3
для маятников №3, №4. Для маятника №2 взять среднеквадратичную
ошибку Sn и значение tα,n из результатов для маятника №1, так как эксперимент проводится в одних и тех же условиях, одним и тем же экспериментатором.Записать результаты измерений для всех маятников и сделать выводы. При этом учитывать число верных знаков в результатах измерений.