Слайд 2
Взаимное пересечение поверхностей
Слайд 3
Линией пересечения двух поверхностей , в общем случае,
является пространственная линия, каждая точка которой может быть представлена
как точка пересечения двух линий, принадлежащих каждой из заданных поверхностей и принадлежащих вспомогательным секущим поверхностям-посредникам, как плоским, так и кривым.
Обязательные требования, предъявляемые к секущим поверхностям-посредникам:
каждая из секущих поверхностей-посредников должна пересекать обе заданные поверхности;
линии, получаемые в результате пересечения должны пересекаться между собой и иметь, по возможности, наиболее простую геометрическую форму.
Слайд 4
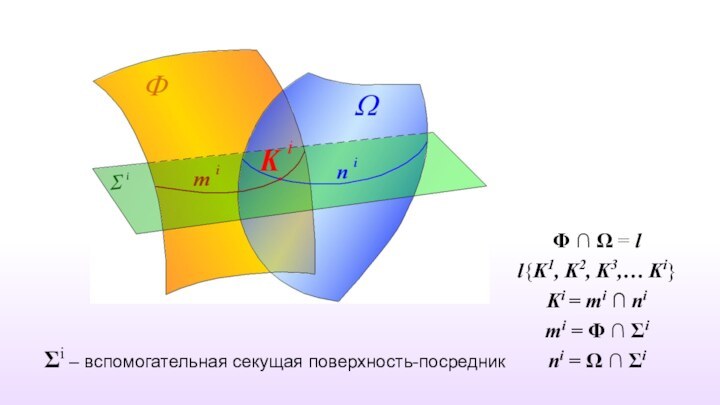
Φ ∩ Ω = l
l{K1, K2, K3,… Ki}
Ki
= mi ∩ ni
mi = Φ ∩ Σi
ni = Ω ∩ Σi
Σi – вспомогательная секущая поверхность-посредник
Слайд 5
Пересечение двух поверхностей может быть
полным и неполным (частичным).
Неполное пересечение называется
врезанием.
Слайд 6
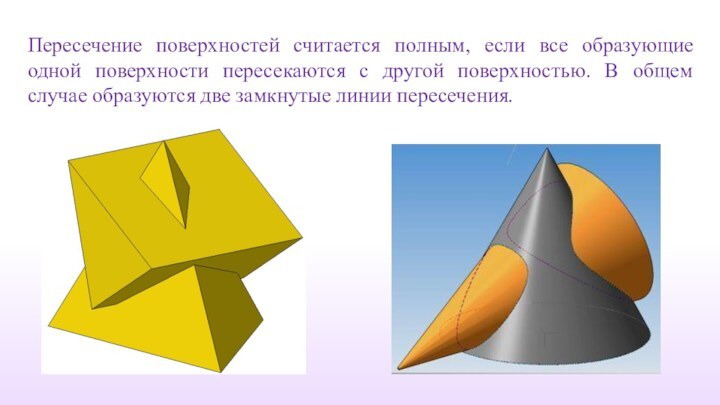
Пересечение поверхностей считается полным, если все образующие одной
поверхности пересекаются с другой поверхностью. В общем случае образуются
две замкнутые линии пересечения.
Слайд 7
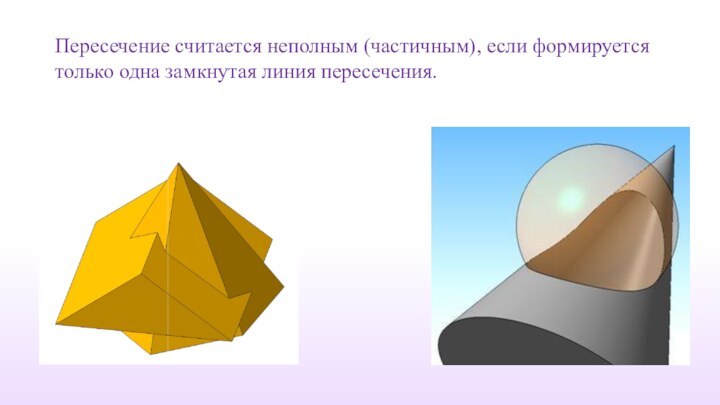
Пересечение считается неполным (частичным), если формируется только одна
замкнутая линия пересечения.
Слайд 8
Взаимное пересечение двух гранных поверхностей
Слайд 9
Линией пересечения двух гранных поверхностей является ломаная прямая
линия, точками излома которой являются точки пересечения ребер одной
гранной поверхности с гранями другой, а линиями, соединяющими эти точки, – отрезки прямых взаимного пересечения граней обеих поверхностей.
Т.е. вся задача на построение линии пересечения двух гранных поверхностей сводится к многократному решению задачи на определение точки пересечения прямой с плоскостью.
Слайд 10
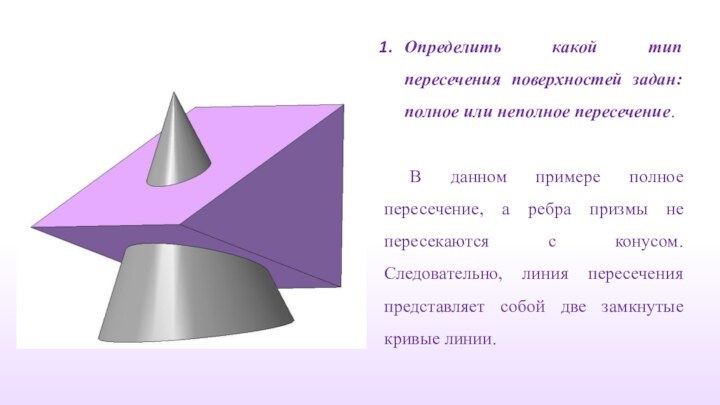
Определить какой тип пересечения поверхностей задан: полное иди
неполное пересечение.
В данном примере полное пересечение, так как
все ребра призмы DEF пересекаются с гранями призмы ABC. Следовательно, линия пересечения распадается на две замкнутые ломаные линии.
D
E
F
А
В
С
Слайд 11
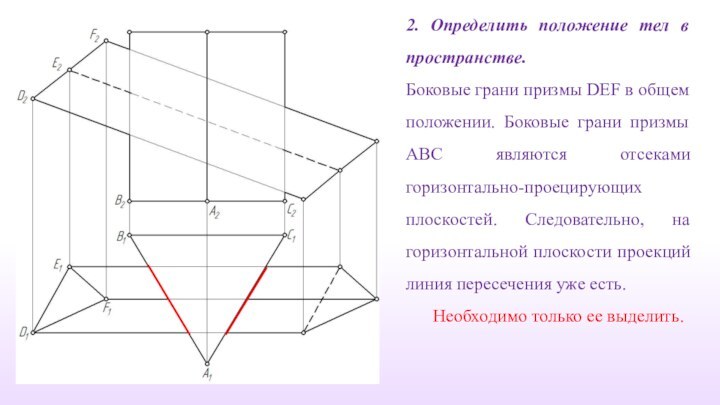
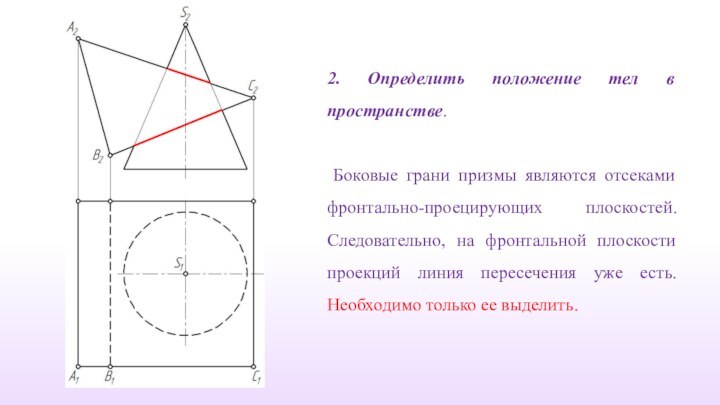
2. Определить положение тел в пространстве.
Боковые грани
призмы DEF в общем положении. Боковые грани призмы ABC
являются отсеками горизонтально-проецирующих плоскостей. Следовательно, на горизонтальной плоскости проекций линия пересечения уже есть.
Необходимо только ее выделить.
Слайд 12
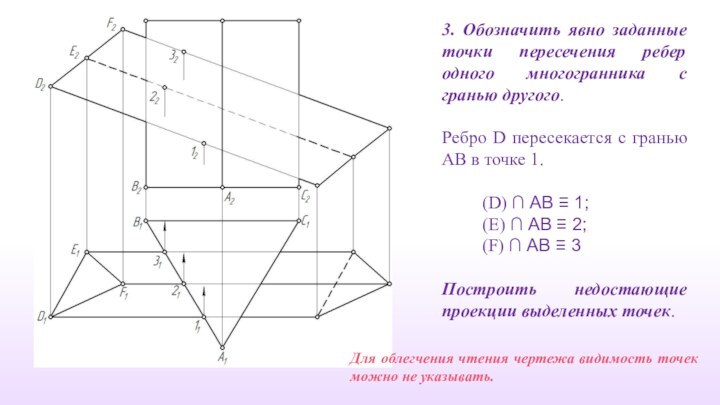
3. Обозначить явно заданные точки пересечения ребер одного
многогранника с гранью другого.
Ребро D пересекается с гранью
АВ в точке 1.
(D) ∩ АВ ≡ 1;
(E) ∩ АВ ≡ 2;
(F) ∩ АВ ≡ 3
Построить недостающие проекции выделенных точек.
Для облегчения чтения чертежа видимость точек можно не указывать.
Слайд 13
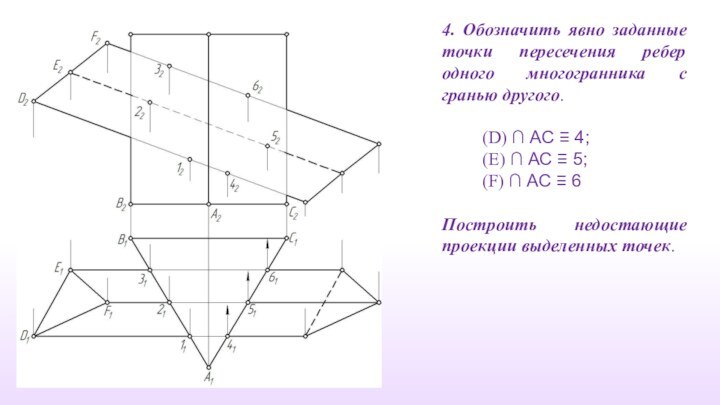
4. Обозначить явно заданные точки пересечения ребер одного
многогранника с гранью другого.
(D) ∩ АС ≡ 4;
(E) ∩ АС ≡ 5;
(F) ∩ АС ≡ 6
Построить недостающие проекции выделенных точек.
Слайд 14
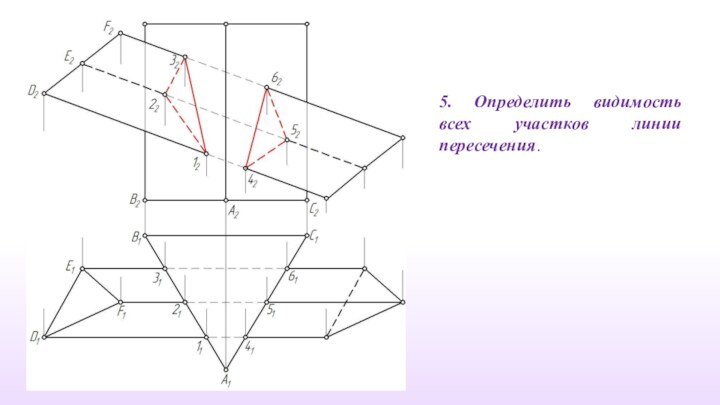
5. Определить видимость всех участков линии пересечения.
Слайд 15
Взаимное пересечение гранной поверхности с кривой поверхностью
Слайд 16
Линия пересечения гранной поверхности с кривой поверхностью представляет
собой
ломаную кривую линию, точками излома которой являются точки
пересечения ребер гранной поверхности с кривой поверхностью, а линиями, соединяющими эти точки – плоские кривые, получаемые при пересечении граней гранной поверхности (отсеков плоскостей) с кривой поверхностью.
кривую линию, если ребра гранной поверхности не пересекаются с кривой поверхностью.
Т.е. задача на построение линии пересечения гранной поверхности с кривой поверхностью сводится к многократному решению двух задач:
определение точек пересечения прямой линии с кривой поверхностью;
построение линии пересечения кривой поверхности плоскостью.
Слайд 17
Определить какой тип пересечения поверхностей задан: полное или
неполное пересечение.
В данном примере полное пересечение, а ребра
призмы не пересекаются с конусом. Следовательно, линия пересечения представляет собой две замкнутые кривые линии.
Слайд 18
2. Определить положение тел в пространстве.
Боковые грани
призмы являются отсеками фронтально-проецирующих плоскостей. Следовательно, на фронтальной плоскости
проекций линия пересечения уже есть. Необходимо только ее выделить.
Слайд 19
3. Обозначить явно заданные точки 1, 2, 3
и 4 пересечения грани ВС многогранника с поверхностью конуса.
Опорные
точки 1 и 2 на очерковых образующих.
Для нахождения точек 3 и 4 вводим вспомогательную плоскость-посредник
α ‖ π1
Построить недостающие проекции выделенных точек.
Слайд 20
4. Обозначить произвольные промежуточные точки 5 и 6
пересечения гран ВС многогранника с кривой поверхностью для уточнения
кривой линии пересечения.
Для нахождения точек 5 и 6 вводим вспомогательную плоскость-посредник
β ‖ π1
Построить недостающие проекции выделенных точек.
Слайд 21
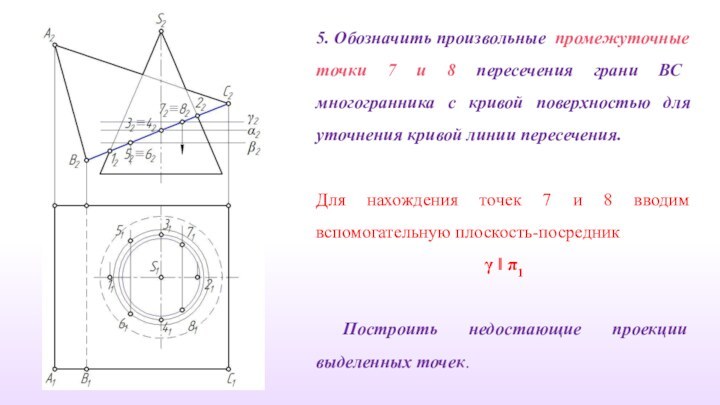
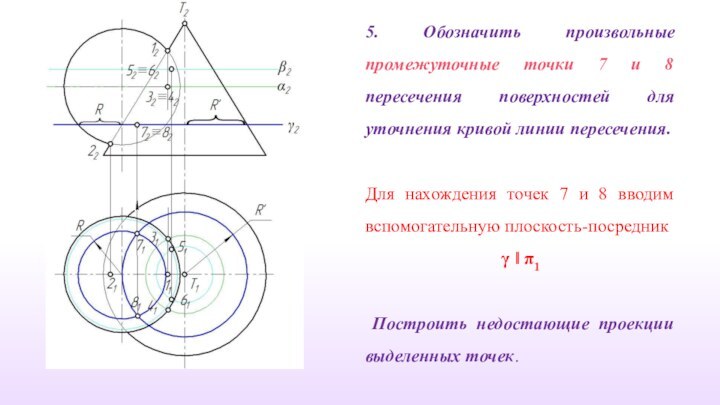
5. Обозначить произвольные промежуточные точки 7 и 8
пересечения грани ВС многогранника с кривой поверхностью для уточнения
кривой линии пересечения.
Для нахождения точек 7 и 8 вводим вспомогательную плоскость-посредник
γ ‖ π1
Построить недостающие проекции выделенных точек.
Слайд 22
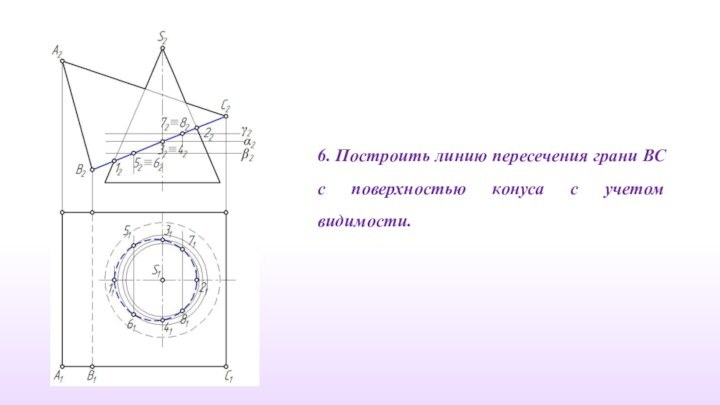
6. Построить линию пересечения грани ВС с поверхностью
конуса с учетом видимости.
Слайд 23
7. Обозначить явно заданные точки 9, 10, 11
и 12 пересечения грани АС многогранника с поверхностью конуса.
Опорные
точки 9 и 10 на очерковых образующих.
Для нахождения точек 11 и 12 вводим вспомогательную плоскость-посредник
δ ‖ π1
Построить недостающие проекции выделенных точек.
Слайд 24
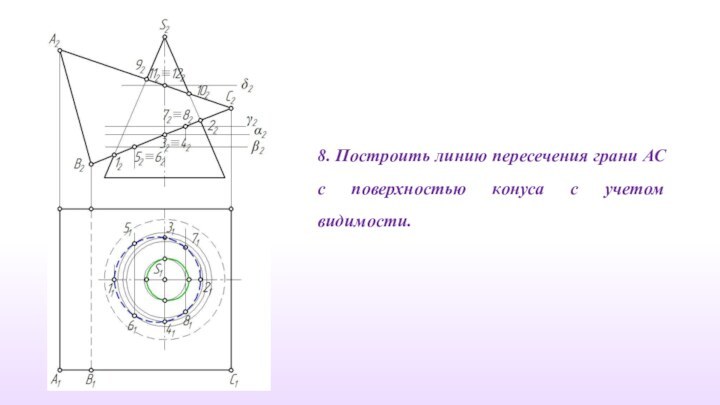
8. Построить линию пересечения грани АС с поверхностью
конуса с учетом видимости.
Слайд 25
Взаимное пересечение кривых поверхностей
Слайд 26
Линией пересечения двух кривых поверхностей является одна или
две пространственные (возможны и плоские) кривые при полном или
неполном пересечении соответственно.
Для получения таких линий должны быть введены вспомогательные секущие поверхности-посредники как плоские, так и кривые.
Обязательные требования, предъявляемые к секущим поверхностям-посредникам:
каждая из секущих поверхностей-посредников должна пересекать обе заданные поверхности;
линии, получаемые в результате пересечения должны иметь наиболее простую геометрическую форму и попарно пересекаться между собой.
Слайд 27
Определение базовых точек линии пересечения
К базовым точкам линии
пересечения относятся:
Точки, определяющие габариты изображения по высоте – точки
А, В.
Точки, определяющие переход видимости – точки D, E.
Точки, определяющие габариты изображения по ширине – точки B, F, G.
Слайд 28
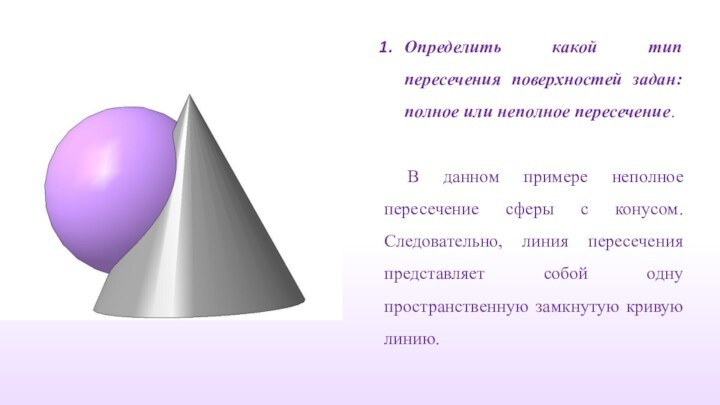
Определить какой тип пересечения поверхностей задан: полное или
неполное пересечение.
В данном примере неполное пересечение сферы с
конусом. Следовательно, линия пересечения представляет собой одну пространственную замкнутую кривую линию.
Слайд 29
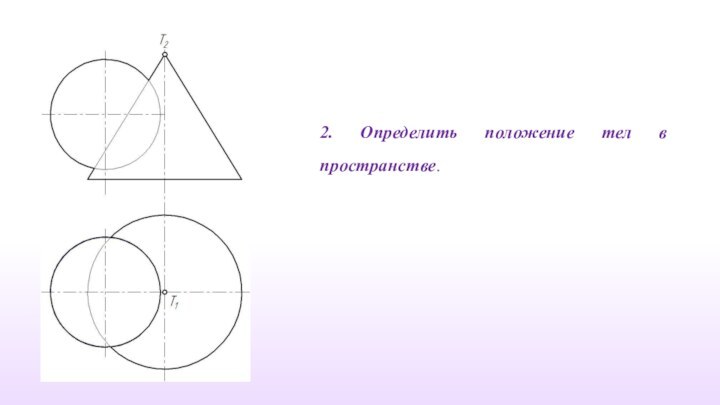
2. Определить положение тел в пространстве.
Слайд 30
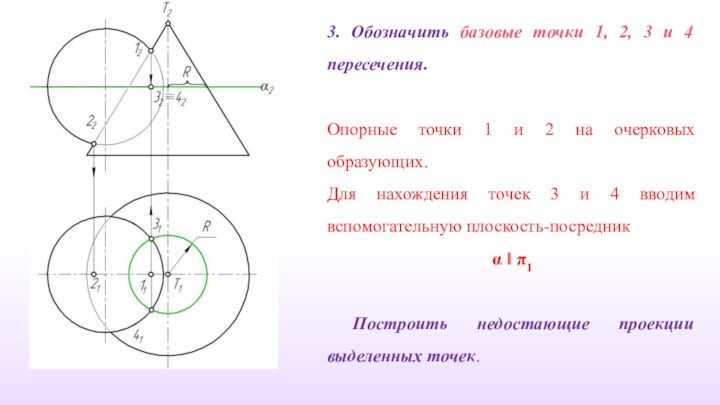
3. Обозначить базовые точки 1, 2, 3 и
4 пересечения.
Опорные точки 1 и 2 на очерковых образующих.
Для
нахождения точек 3 и 4 вводим вспомогательную плоскость-посредник
α ‖ π1
Построить недостающие проекции выделенных точек.
Слайд 31
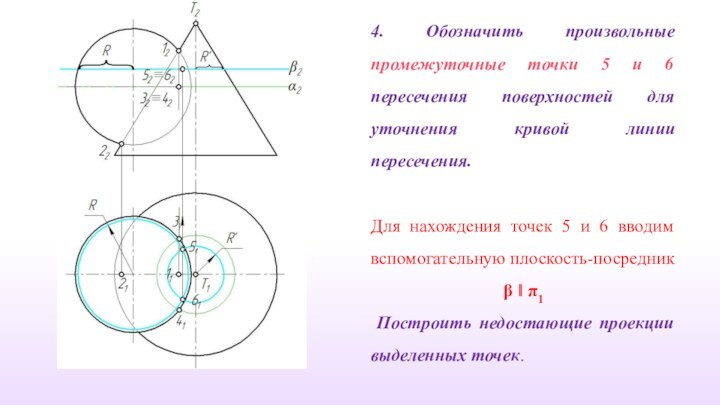
4. Обозначить произвольные промежуточные точки 5 и 6
пересечения поверхностей для уточнения кривой линии пересечения.
Для нахождения точек
5 и 6 вводим вспомогательную плоскость-посредник
β ‖ π1
Построить недостающие проекции выделенных точек.
Слайд 32
5. Обозначить произвольные промежуточные точки 7 и 8
пересечения поверхностей для уточнения кривой линии пересечения.
Для нахождения точек
7 и 8 вводим вспомогательную плоскость-посредник
γ ‖ π1
Построить недостающие проекции выделенных точек.
Слайд 33
6. Построить линию пересечения поверхности сферы с поверхностью
конуса с учетом видимости.
Слайд 34
Частные случаи взаимного пересечения двух поверхностей вращения
Слайд 35
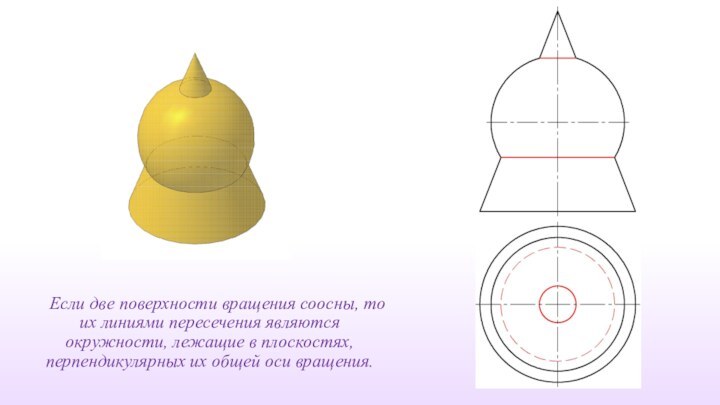
Если две поверхности вращения соосны, то их линиями
пересечения являются окружности, лежащие в плоскостях, перпендикулярных их общей
оси вращения.
Слайд 36
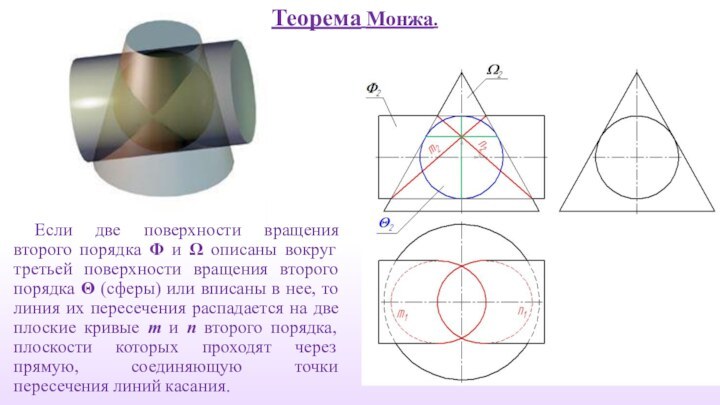
Если две поверхности вращения второго порядка Φ и
Ω описаны вокруг третьей поверхности вращения второго порядка Θ
(сферы) или вписаны в нее, то линия их пересечения распадается на две плоские кривые m и n второго порядка, плоскости которых проходят через прямую, соединяющую точки пересечения линий касания.
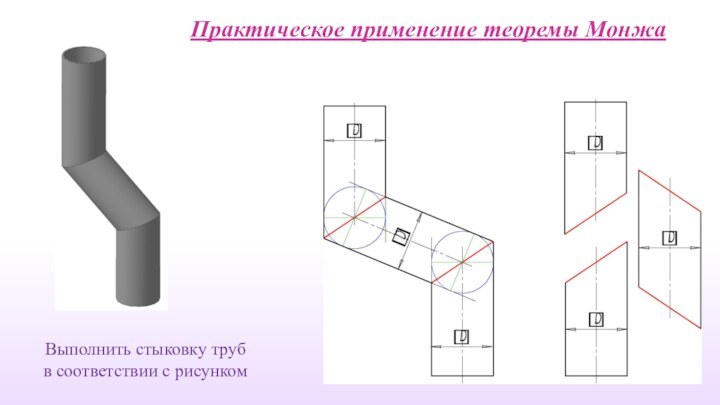
Теорема Монжа.