Слайд 2
В работе дается ответ на вопрос:
действительно ли прогрессии играют большую роль в повседневной жизни?
Для этого сделан анализ сделан исторический экскурс для установления авторства теории о прогрессиях. Приведены примеры применения прогрессий в различных отраслях хозяйства. Сделан анализ влияния размножения живых организмов в геометрической прогрессии на жизнь на Земле.
Аннотация проекта
изучаем прогрессии: дали определение, научились находить по формулам любой
член прогрессии, сумму первых членов прогрессии. Найдя ответы на вопросы: имеет ли это какое - либо практическое значение и как давно люди знают последовательности, как возникло это понятие, мы подтвердим или опровергнем утверждение о том, что математика – наука очень древняя и возникла она из практических нужд человека, что алгебра является частью общечеловеческой культуры.
Актуальность исследования
(Почему это важно для нас?):
Слайд 4
Проблемный вопрос:
Действительно ли
прогрессии играют
большую роль в повседневной жизни?
Слайд 5
Объект исследования: последовательности: арифметическая и геометрическая прогрессии.
Предмет исследования:
практическое применение этих прогрессий
Слайд 6
Гипотеза исследования:
На уроках математики мы много раз слышали
о том, что математика – наука очень древняя и возникла она из практических нужд человека. Видимо, и прогрессии имеют определенное практическое значение.
Слайд 7
Цель исследования:
установить картину возникновения
понятия прогрессии
и выявить примеры
их применения.
Слайд 9
По страницам
школьных
учебников
Последовательности:
путешествие
в глубь веков
Прогрессии
в природе
Прогрессии
в банковских расчетах
и в промышленности
Прогрессии
в старых
учебниках по математике
Прогрессии в книгах
по занимательной математике
Выводы и источники информации
Слайд 10
Задачи с практическим содержанием
из современных учебников по алгебре
Алгебра. 9 класс, : Учебник для общеобразовательных учреждений /
Макарычев Ю.Н., Миндюк Н.Г., Суворова С.Б./ под ред. С.А. Теляковского . -М.: Просвещение, 2009, -271с. № 581, 582, 583, 598, 614, 616, 629,637, 638, 639, 640, 641, 642, 674 (14 задач).
Алгебра. 9 класс, : Учебник для общеобразовательных учреждений / Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феактистов И.Е. . -М.: Мнеозина, 2008, -447с. № 698, 699,702,725,734, 788, 789 (7 задач)
Математика. Алгбра.Функции. Анализ данных.9 кл.: Учебник для общеобразовательных учебных заведений/ Г.В. Дорофеев , С.Б. Суворова, Е.А. Бунимович, Л.В. Кузнецова, С.С. Минаева; под ред. Г.В. Дорофеева.-М.:Дрофа, 2000,-352с.: № 511, 514, 515, 527(в-г), 539, 540, 542, 543, 563-566, 573-578, 591, 595 - 601, 604, 605, 620,622-626, 628, 638 - 643, 645, 647, 648, 650, 651, 653-659 (54 задачи).
Алгебра. 9 класс, в 2ч. Ч.2. Учебник для общеобразовательных учреждений / Мордкович А.Г., П.В. Семенов , -М.: Мнемозина, 2010, -224с : № 16.63-16.66, 17.35, 17.46, 17.51. 17.58 (8 задач).
Слайд 11
Арифмети́ческая прогре́ссия —
числовая
последовательность, в которой каждое последующее число, начиная со второго,
получается из предыдущего увеличением его на определённое число.
Имеет вид: a1, a1+d, a1+2d, a1+3d, …, a1+(n-1)d,…
Геометри́ческая прогре́ссия — последовательность чисел, в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число.
Имеет вид: b1, b1q, b1q2, b1q3,… ,b1qn-1,…
Слайд 12
Вывод характеристических свойств
арифметической и геометрической прогрессий
an-an-1=d;
an+1-an=d;
an-an-1=an+1-an
2an=an+1+an-1
bn:bn-1=d;
bn+1:bn=d;
bn:bn-1=bn+1:bn
bn2=bn+1·bn-1
Слайд 13
Формулы
Арифметическая прогрессия
Геометрическая прогрессия
Слайд 14
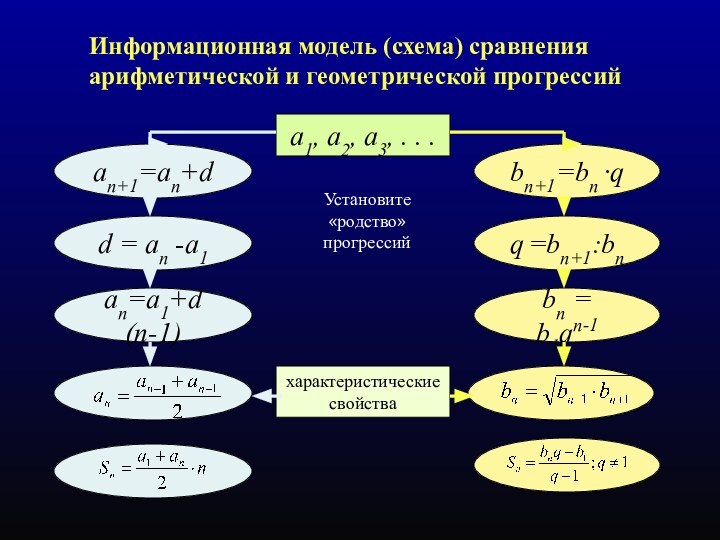
Информационная модель (схема) сравнения арифметической и геометрической прогрессий
Установите
«родство»
прогрессий
a1,
a2, a3, . . .
an+1=an+d
bn+1=bn ·q
an=а1+d (n-1)
bn =
b1qn-1
d = an -а1
q =bn+1:bn
характеристические
свойства
Слайд 15
Сравнение арифметической и
геометрической прогрессий
an+1=an+d
bn+1=bn ·q
an=а1+d (n-1)
bn
= b1qn-1
d = an -а1
q =bn+1:bn
Прочитав определения
арифметической
и геометрической
прогрессий
можно обратить внимание
на то, что они похожи.
Надо лишь заменить
сложение
умножением.
А зная формулу n-го члена
арифметической
прогрессии,
можно получить
формулу
для геометрической
прогрессии,
если заменить сложение
умножением и умножение –
возведением в степень
Слайд 16
Определения (оба сразу!)
Числовая последовательность, каждый
член которой, начиная
со второго,
равен предшествующему члену,
сложенному с одним и
тем же числом,
умноженному на одно и то же число,
называется арифметической прогрессией
геометрической
Слайд 17
“Родство” прогрессий становится еще более заметным,
если сравнить
их характеристические свойства.
Здесь тоже достаточно заменить сложение умножением,
а деление на два - извлечением корня второй степени,
и из характеристического свойства арифметической прогрессии
получится характеристическое свойство геометрической прогрессии
Слайд 18
Характеристические свойства арифметической и геометрической прогрессий (оба сразу!)
Любой
член арифметической прогрессии,
геометрической
начиная со второго, является
средним
арифметическим
геометрическим
предшествующего и последующего членов.
Слайд 19
Имеют ли
арифметическая и геометрическая прогрессии
прикладное значение?
Слайд 20
Задача № 468
[Алгебра. 9 класс, в 2ч.
Ч.2. Учебник для общеобразовательных учреждений / Мордкович А.Г., П.В.
Семенов , -М.: Мнемозина, 2010, -224с.(с.100)]
В соревновании по стрельбе за каждый промах в серии из 25 выстрелов стрелок получал штрафные очки: за первый промах — одно штрафное очко, за каждый последующий — на 0,5 очка больше, чем за предыдущий. Сколько раз попал в цель стрелок, получивший 7 штрафных очков?
Решение. Составим математическую модель задачи. Система штрафных очков составляет арифметическую прогрессию, первый член которой равен 1, а разность – 0,5. Сумма первых n членов ( количество промахов) равно 7. Найдем число промахов - n.
Слайд 21
Задача №469.
[Алгебра. 9 класс, в 2ч. Ч.2.
Учебник для общеобразовательных учреждений/ Мордкович А.Г., П.В. Семенов ,
-М.: Мнемозина, 2010, -224с.(с.100)
Больной принимает лекарство по следующей схеме: в первый день он принимает 5 капель, а в каждый следующий день — на 5 капель больше, чем в предыдущий. Приняв 40 капель, он 3 дня пьет по 40 капель лекарства, а потом ежедневно уменьшает прием на 5 капель, доведя его до 5 капель. Сколько пузырьков лекарства нужно купить больному, если в каждом содержится 20 мл лекарства (что составляет 250 капель)?
Слайд 22
Решение. Составим математическую модель задачи:
5, 10, 15,…,40, 40, 40, 35, 30,…,5
ап=а1+d(n-1),
40=5+5(п-1),
п=8,
Sп=((a1+aп)n)/2, S8 =(5+40)·8:2=180,
180 капель больной принимал по схеме в первый период и столько же по второй период. Всего он принял 180+40+180=400(капель), всего больной выпьет 400:250=1,6 (пузырька). Значит, надо купить 2 пузырька лекарства.
возрастающая
арифметическая
прогрессия
а1=5, d=5
убывающая
арифметическая
прогрессия
с1=5, d=-5
Слайд 23
Задача №470
[Алгебра. 9 класс, в 2ч. Ч.2.
Учебник для общеобразовательных учреждений/ Мордкович А.Г., П.В. Семенов ,
-М.: Мнемозина, 2010, -224с.(с.100)
Улитка ползет по дереву. За первую минуту она проползла 30 см, а за каждую следующую минуту — на 5 см больше, чем за предыдущую. За какое время достигнет улитка вершины дерева длиной 5,25 м, если считать, что движение начато от его основания?
Решение. a1 =30, d=5, Sn= 525, n>0.
Sn= (2a1+ d (n-1))n:2; 525= (2·30+ 5 (n-1))n:2; 1050= (60+ 5 (n-1))n;
1050= 55 n + 5n2;
n2 +11 n -210=0, n1=-21, n2=10 (n>0).
Улика достигнет вершины за 10 дней.
Слайд 24
Задача № 471
[Алгебра. 9 класс, в 2ч.
Ч.2. Учебник для общеобразовательных учреждений/ Мордкович А.Г., П.В. Семенов
, -М.: Мнемозина, 2010, -224с.(с.100)
Альпинисты в первый день восхождения поднялись на высоту 1400 м, а затем каждый следующий день они проходи ли на 100 м меньше, чем в предыдущий. За сколько дней они покорили высоту в 5000 м?
Решение. Составим математическую модель задачи: 1400, 1300, …, 1400-100(n-1). a1=1400; d=-100, Sn=5000. Надо найти n.
Sn= (2a1+ d (n-1))n:2;
5000= (2·1400-100 · (n-1)) n:2; Условию задачи удовлетворяет
10000= (2800-100 n+100) n; n=4 ( при n=25 аn=-1000, но аn>0)
10000= (2900-100 n) n; Значит, альпинисты покорили
100 n2-2900 n+10000=0; высоту за 4 дня.
n2-29 n+100=0; n=25, n=4. Ответ: за 4 дня.
Слайд 25
Задача № 472
[Алгебра. 9 класс, в 2ч.
Ч.2. Учебник для общеобразовательных учреждений / Мордкович А.Г., П.В.
Семенов , -М.: Мнемозина, 2010, -224с.(с.100)
За изготовление и установку самого нижнего железобетонного кольца колодца заплатили 26 условных единиц (у. в.). а за каждое следующее кольцо платили на 2 у. е. меньше, чем за предыдущее. Кроме того, по окончании работы было уплачено ещё 40 у. е.. Средняя стоимость изготовления и установки кольца оказалась равной 22 и 4/9 у. е.. Сколько колец было установлено?
Решение. а1=26, d=-2.
9n2-41n-360=0,
n1=9, , n - целое число.
Было изготовлено и установлено 9 колец.
Слайд 26
Задача № 614.
[Алгебра. 9 класс, : Учебник для
общеобразовательных учреждений/ Макарычев Ю.Н., Миндюк Н.Г., Суворова С.Б. .
-М.: Просвещение, 2009, -271с.(с.152)
При свободном падении тело прошло в первую секунду 5м, а в каждую следующую на 10м больше. Найдите глубину шахты, если свободно падающее тело достигло его дна через 5 с. после начала падения.
Решение. Составим математическую модель задачи:
впервую секунду 5м,
во вторую секунду 15м,
в третью секунду 25м,
в четвертую секунду 35м,
в пятую секунду 45м.
Всего за пять секунд 5+15+25+35+45=125(м).
Ответ: глубина шахты 125м.
Слайд 27
Задача № 614.
[Алгебра. 9 класс,: Учебник для
общеобразовательных учреждений/ Макарычев Ю.Н., Миндюк Н.Г., Суворова С.Б. .
-М.: Просвещение, 2009, -271с.(с.152)
При свободном падении тело прошло в первую секунду 5м, а в каждую следующую на 10м больше. Найдите глубину шахты, если свободно падающее тело достигло его дна через 5 с. после начала падения.
Решение. Составим математическую модель задачи: а1=5, d=10. а5=а1+4d; а5=45.
S5=(a1+a5)·n:2; S5=(5+45)·5:2=125;
глубина шахты 125м.
Ответ: 125м.
Слайд 28
Задача. При хранении бревен строевого леса их укладывают
как показано на рисунке. Сколько брёвен находится в одной
кладке, если в ее основании положено 12 бревен?
Решение. Составим математическую модель задачи: 1, 2, 3, 4,…,12. Это арифметическая прогрессия, а1=1, d=1,аn=12. Надо найти n.
аn=a1+d(n-1); 12=1+1(n-1); n=12.
Sn=(a1+an)∙n:2; Sn=(1+12)·12:2; Sn=78.
В одной кладке находится 78 бревен.
Ответ: 78 бревен.
Слайд 29
Задача
Три числа составляют арифметическую прогрессию. Найдите эти числа,
если их сумма равна 27, а при уменьшении первого
числа на 1, уменьшении второго на 3 и при увеличении третьего на 3, получили геометрическую прогрес.
Слайд 31
Если d=6, то а1=3, а2=9,а3=15.
Если d=-10, то а1=19,
а2=9,а3=-1.
Тогда, если арифметическая прогрессия
3, 9, 15, то геометрическая
прогрессия 2, 6, 18. Если арифметическая прогрессия 19, 9, -1, то геометрическая прогрессия 18, 6, 2.
Ответ: 3, 9,15 или 19, 9, -1.
Слайд 32
1. Чтобы отправить четыре бандероли, требуется четыре разные
почтовые марки на общую сумму 120 рублей. Цены марок
составляют арифметическую прогрессию. Сколько стоит самая дорогая марка, если она в три раза дороже самой дешевой?
2. В первом ряду кинотеатра 21 кресло, В каждом последующем ряду на 2 кресла больше, чем в предыдущем. Сколько кресел в 40 ряду?
3. Длины сторон выпуклого многоугольника образуют арифметическую прогрессию с разностью 4см. Периметр многоугольника равен 75см, а наибольшая сторона равна 23см. Сколько сторон имеет данный многоугольник.
Еще задачи с практическим содержанием
Слайд 33
Сделав анализ задач на прогрессии
с практическим содержанием мы увидели, что прогрессии встречаются при
решении задач в медицине, в строительстве, в банковских расчетах, в живой природе, в спортивных соревнованиях и в других жизненных ситуациях. Следовательно, нам необходим навык применения знаний, связанных с прогрессиями.
Слайд 34
Последовательности:
путешествие
в глубь веков
Слайд 35
Первые теоретические сведения, связанные
с прогрессиями, дошли до нас в документах Древней Греции.
В Древнем Египте в V в до н.э. греки знали прогрессии и их суммы:
1+2+3+…+n = =2+4+6+…+2n = n·(n+1).
Некоторые формулы, относящиеся к прогрессиям, были известны китайским и индийским ученым (V в.)
Слайд 36
Примеры отдельных арифметических и геометрических прогрессий можно встретить
еще в древневавилонских и греческих надписях, имеющих возраст около
четырех тысячелетий и более. В древней Греции еще пять столетий до н.э. были известны такие суммы:
1+2+3+…+n=½n(n+1);
1+3+5+…+(2n-1)=n2;
2+4+6+…+2n=n(n+1).
Слайд 37
В клинописных табличках вавилонян, как
и в египетских папирусах, относящихся ко второму тысячелетию до
нашей эры, встречаются примеры арифметических и геометрических прогрессий. Вот пример задачи из египетского папируса Ахмеса: «Пусть тебе сказано: раздели 10 мер ячменя между 10 человеками и, разность же между каждым человеком и его соседом равна меры».
Задачи на прогрессии, дошедшие до нас из древности, были связаны с запросами хозяйственной жизни: распределение продуктов, деление наследства и другие.
В трудах АРХИМЕДА (ок. 287-212 гг. до н.э.) излагаются первые сведения о прогрессиях.
Слайд 38
Как Архимед вычислял площадь круга…
Вначале Архимед вписывал в круг шестиугольник,
затем на каждой стороне построил равнобедренный треугольник – получался двенадцатиугольник. Постепенно удваивая число сторон, Архимед получил 24-угольник, 48-угольник и, наконец, 96-угольник. Построенные многоугольники все более и более покрывали собой площадь круга, как бы постепенно “исчерпывая” ее. Между прочим, этот метод нахождения площади круга до сих пор, через 2200 лет после смерти Архимеда, излагается в современных школьных учебниках геометрии.
Слайд 39
В ходе своих исследований
Архимед нашел сумму бесконечной геометрической прогрессии со знаменателем 1/4,
что явилось первым примером появления в математике бесконечного ряда…
.
Слайд 40
В “Исчислении песчинок” Архимед впервые сопоставляет арифметическую и
геометрическую прогрессии, устанавливает между ними связь:
1, 2, 3, 4,
5, …
10, 102, 103, 104, 105, …
и указывает на связь между ними, например:
103·105=103+5=108,
т.е. для умножения двух членов геометрической прогрессии достаточно сложить соответствующие члены арифметической прогрессии и взять полученную сумму в качестве показателя 10.
Слайд 41
Одно из доказательств Архимеда, изложенное в его
произведении “Квадратура параболы”, сводится к суммированию бесконечно убывающей геометрической
прогрессии:
.
Слайд 42
Для решения некоторых задач из геометрии и механики
Архимед вывел формулу суммы квадратов натуральных чисел, хотя ею
пользовались и до него:
.
Слайд 43
Пифагор и последовательности
Пифагор (IV в. до н. э.)
и его ученики рассматривали последовательности, связанные с геометрическими фигурами.
Подсчитывая число кружков в треугольниках, квадратах, пятиугольниках, они получали:
- последовательность (ап) треугольных чисел 1, 3, 6, 10, 15, ... ;
- последовательность (bп) квадратных чисел 1, 4, 9, 16, 25, ... ;
- последовательность (сп) пятиугольных чисел 1, 5, 12, 22, 35, ...
Слайд 44
В древности вычислители часто
считали с помощью камешков и, естественно, отмечали случаи, когда
камешки можно было сложить в виде правильной фигуры.
Слайд 45
Зададим эту последовательностей формулой п-ого члена.
Последовательность (ап) треугольных
чисел получается из последовательности натуральных чисел 1, 2, 3,
... , т. е. из арифметической прогрессии, в которой первый член и разность равны 1, следующим образом:
а1 = 1, а2 = 1 + 2, а3 = 1 + 2 + 3, ап = 1 + 2 + 3 + ... + п.
Значит, ап = (1 + п ):2·п.
Слайд 46
Последовательность (bп) квадратных чисел аналогичным способом получается из
последовательности нечетных чисел 1, 3, 5, ... , т.
е. из арифметической прогрессии, первый член которой равен 1 и разность равна 2:
b1= 1, b2 = 1 + 3, bз = 1 + 3 + 5, …, bn = 1 + 3 + 5 + ... + 2п- 1.
Следовательно, bn =(1+2n-1):2·n; bn=n2 . Мы пришли к формуле, очевидной для последовательности квадратных чисел.
Слайд 47
Последовательность (cп) пятиугольных чисел аналогичным способом получается из
последовательности нечетных чисел 1, 4, 7, ... , т.
е. из арифметической прогрессии, первый член которой равен 1 и разность равна 3: с1= 1, с2 = 1 + 4,
bз = 1 + 4 + 7, …, сn = 1 + 4 + 7 + ... +(1+3( п- 1)).
Следовательно, сn =(1+1+3( п- 1)):2·n; сn=(3n-1)·n/ 2
Слайд 48
У европейцев правило для нахождения суммы членов любой
арифметической прогрессии встречается впервые в сочинении Леонардо Пизанского «Книга
об абаке» (1202 г.)
Последовательность Фибоначчи
Слайд 49
"Книге абака" представляет собой объемный труд, содержащий
почти все арифметические и алгебраические сведения того времени и
сыгравший значительную роль в развитии математики в Западной Европе в течении нескольких следующих столетий. В частности, именно по этой книге европейцы познакомились с индусскими (арабскими) цифрами. Сообщаемый в этой книге материал поясняется на примерах задач, составляющих значительную часть этого тракта.
Слайд 50
Наиболее известной из
сформулированных Фибоначчи задач является "задача о размножении кроликов", которая
привела к открытию числовой последовательности 1, 1, 2, 3, 5, 8, 13, ..., именуемой впоследствии "рядом Фибоначчи".
Слайд 51
Задача Фибоначчи :
Некто поместил
пару кроликов в некоем месте, огороженном со всех сторон
стеной, чтобы узнать, сколько пар кроликов родится при этом в течении года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения.
Слайд 52
Ясно, что если считать первую пару кроликов новорожденными,
то на второй месяц мы будем по прежнему иметь
одну пару; на 3-й месяц- 1+1=2; на 4-й- 2+1=3 пары(так как из двух имеющихся пар потомство дает лишь одна пара); на 5-й месяц- 3+2=5 пар (лишь 2 родившиеся на 3-й месяц пары дадут потомство на 5-й месяц); на 6-й месяц- 5+3=8 пар (так как потомство дадут только те пары, которые родились на 4-м месяце) и т. д.
Слайд 53
Чтобы ответить на вопрос задачи, воспользуемся следующей схемой.
Кружочек — это пара кроликов. Стрелка, направленная вниз, указывает
на эту же пару в следующем месяце; а стрелка, направленная вправо, указывает на появившееся потомство этой пары.
Слайд 54
«Сколько пар кроликов в один год от одной
пары родится».
Ряд чисел 0, 1, 1, 2, 3, 5,
8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д.,
Слайд 55
Таким образом, если обозначить число пар кроликов, имеющихся
на n- м месяце через Uk , то u1=1,
u2=1, u3=2, u4=3, u5=5, u6=8, u7=13, u8=21 и т. д., причем образование этих чисел регулируется общим законом:
un =un-1 + un-2 при всех n >2,
ведь число пар кроликов на n-1 м месяце равно числу n-2 пар кроликов на предшествующем месяце плюс число вновь родившихся пар, которое совпадает с числом un-2 пар кроликов, родившихся на n-2 ом месяце (так как лишь эти пары кроликов дают потомство).
Слайд 56
Числа un, образующие последовательность
1, 1, 2, 3,
5, 8, 13, 21, 34, 55, 89, 144, 233,...
называются
числами Фибоначчи", а сама последовательность ––
последовательностью Фибоначчи.
Суть последовательности Фибоначчи в том, что
начиная с третьего числа каждое следующее число
получается сложением двух предыдущих .
Слайд 57
Определение последовательности Фибоначчи
Числа Фибоначчи — элементы числовой последовательности
1, 1, 2, 3, 5, 8, 13, 21, 34,
55, 89, 144, 233, 377, 610, 987, 1597 … в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского. Построение последовательности:
Слайд 58
Простейшие свойства последовательности
1.Сумма первых n-чисел Фибоначчи: u1+u2+…+un=un+2 -1.
2.Сумма
чисел Фибоначчи с нечетными номерами:
u1+u3+u5+…+u2n-1=u2n.
3.Сумма чисел Фибоначчи с четными номерами:
u2+u4+…+u2n=u2n+1 -1.
4.Сумма квадратов первых n-чисел Фибоначчи:
Слайд 59
5.
6.
7.
8.
9.
10. В ряду Фибоначчи каждое третье число –
чётное, каждое четвёртое делится на 3, каждое пятое –
на 5, каждое пятнадцатое на 10.
Слайд 60
Следствия свойства 11:
1)Пусть в формуле (*) m=n
u2n=un-1un +unu n+1 или u2n=un(un-1+un+1) так как un=un+1-un-1u2n
= (un+1-un-1)(un+1+un-1) или u2n=(un+1)2-(un-1)2.
Значит, разность квадратов двух чисел Фибоначчи, номера которых отличаются на 2, есть снова число Фибоначчи.
2)Пусть m=2n u3n=(un+1)3+(un )3-(un-1)3.
11. un+m=un-1um+unum+1 (*)
Слайд 61
Интересно было бы уметь сразу получить любой член
ряда , зная лишь номер n его места. Оказывается,
это вполне возможно, но здесь мы столкнемся с одной из удивительных неожиданностей, которые нередки в математике. Любой член ряда Фибоначчи- число целое, номер места - тоже число целое.
Естественно было бы ожидать, что любой член ряда получается в зависимости от номера и занимаемого им места при помощи действий только над целыми числами (например, как в прогрессиях). Но это не так. Не только целые числа, но даже все целые и дробные (рациональные) бессильны образовать интересующую нас формулу. Из затруднительного положения помогают выйти два иррациональных числа:
Если n - номер места, то любой член ряда
Фибоначчи можно получить по формуле
Слайд 62
Золотое сечение и Фибоначчи
Отношение смежных чисел ряда приближается
к отношению золотого деления. Так, 21 : 34 = 0,617, а
34 : 55 = 0,618. Это отношение обозначается символом Ф. Только это отношение – 0,618 : 0,382 – дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему.
Так имя итальянского математика монаха Леонардо Фибоначчи косвенным образом связано с историей золотого сечения.
Слайд 63
Сведения из истории
Сами по себе прогрессии известны
так давно, что конечно, нельзя говорить о том, кто
их открыл. Ведь уже натуральный ряд есть арифметическая прогрессия с первым членом и разностью, равных 1.
О том, как давно была известна геометрическая прогрессия, свидетельствует знаменитое предание о создании шахмат. Рассказывают, что индийский принц Сирам рассмеялся, услышав, какую награду попросил у него изобретатель шахмат: за первую клетку шахматной доски – одно зерно, за вторую – два, за третью – четыре, за четвертую – восемь и так до 64-го поля. Здесь явная геометрическая прогрессия с первым членом, равным 1, и знаменателем, равным 2.
Слайд 64
Сведения из истории
В сочинении Евклида «Начала» (около
300 лет до н.э.) в словесной форме содержится теорема
относительно геометрической прогрессии, которую можно выразить следующим равенством:
Этот результат только по внешнему виду отличается от современной формулы:
Слайд 65
В Германии молодой
Карл Гаусс (1777-1855) нашел моментально сумму всех натуральных чисел
от 1 до 100, будучи ещё учеником начальной школы.
1+2+3+4+…+98+99+100 =
= (1+100)+(2+99)+(3+98)+…+(50+51)=
=101x50 =5050.
Общее правило для суммирования любой конечной геометрической прогрессии встречается в книге Н. Шюке «Наука о числах», увидевшей свет в 1484 году.
Слайд 66
Общая формула для вычисления суммы любой бесконечно убывающей
геометрической прогрессии была выведена в первой половине XVII века
несколькими математиками (среди них был французский математик Пьер Ферма)
Слайд 67
На связь между прогрессиями первым обратил внимание великий
Архимед.
В печати же эти мысли отчетливо прозвучали
лишь в 1544 г., когда вышла книга немецкого математика Михаила Штифеля «Общая арифметика», который составил такую таблицу:
Слайд 68
-В верхней строчке написана арифметическая прогрессия с разностью
1. В нижней строчке – геометрическая прогрессия со знаменателем
2.
Слайд 69
Пример №1.
Надо умножить 1/2 на 128.
Обращаем внимание, что в таблице над 1/2 написано -1,
а над 128 написано 7. Сложим эти числа, получим 6, а под шестеркой читаем 64. Это и есть искомое произведение.
Слайд 70
Пример №2. Разделим 32 на 8. Обращаем внимание,
что в таблице над 32 написано 5, а над
8 написано 3. Вычтем эти числа 5-3, получим 2, а под двойкой читаем 4. Это и есть искомое частное.
Слайд 71
Если вспомнить тождества an·am=an+m и am:an=am-n, то нижнюю
строчку таблицы Штифеля можно переписать так:
Слайд 72
Теперь можно увидеть,
что, если показатели степени составляют арифметическую прогрессию, то сами
степени составляют геометрическую прогрессию.
Заметим, что с помощью таблицы можно возводить в степень извлекать корни. Например, чему равно 43? Против 4 читаем 2,умножаем 2 на 3, получаем 6, против 6 читаем 64, значит, 43 = 64.
А чему равен корень четвертой степени из 256? Делим 8 на 4, против 2 читаем 4, значит, корень четвертой степени из 256 равен 4.
Слайд 73
В начале XIII века в
городе Пизе (Италия) жил большой знаток всевозможных соотношений между
числами и весьма искусный вычислитель Леонардо (с добавлением к его имени Пизанский). Его звали еще Фибоначчи, что значит сын Боначчи. В 1202 году он издал книгу на латинском языке под названием «Книга об абаке» (Incipit Liber, Abbaci compositus a Leonardo filius Bonacci Pisafto), которая содержала в себе всю совокупность знаний того времени по арифметике и алгебре. Это была одна из первых книг в Европе, учившая употреблять десятичную систему счисления. Автор познакомил Европу с индийскими (арабскими) цифрами. Это был труд, в котором были собраны все известные на то время задачи. Книга Леонардо Пизанского получила широкое распространение и более двух веков являлась наиболее авторитетным источником знаний в области чисел.
Историческая справка
Слайд 74
Одна из задач, рассмотренная Фибоначчи, называется
"задачей о поиске наилучшей системы гирь для взвешивания на
рычажных весах" или просто "задачей о гирях". В русской историко-математической литературе "задача о гирях" известна под названием "задачи Баше-Менделеева", названной так в честь французского математика 17 в. Баше де Мезириака, который разместил эту задачу в своем "Сборнике приятных и занимательных задач" (1612 г.) и блестящего русского химика Дмитрия Ивановича Менделеева, который интересовался этой задачей будучи директором Главной Палаты мер и весов России.
Слайд 75
Сущность "задачи Баше-Менделеева" состоит в следующем: при какой
системе гирь, имея их по одной, можно взвесить всевозможные
грузы Q от 0 до максимального груза Qmax, чтобы значение максимального груза Qmax было бы наибольшим среди всех возможных вариаций? Известно два варианта решения этой задачи: (1) когда гири позволено класть на свободную чашу весов; (2) когда гири позволяется класть на обе чаши весов. В первом случае "оптимальная система гирь" сводится к двоичной системе гирь: 1, 2, 4, 8, 16, ..., а появляющийся при этом "оптимальный" алгоритм или способ измерения рождает двоичную систему счисления, лежащую в основе современных компьютеров. Во втором случае наилучшей является троичная система гирь: 1, 3, 9, 27, 81, ..., а возникающий при этом способ измерения рождает троичную симметричную систему счисления, которая была применена в троичном компьютере Сетунь, построенном в 50-е годы в МГУ.
Слайд 76
Еще одна задача интересна в исторической связи и
носит имя "задачи о семи старухах". Старухи направляются в
Рим, каждая имеет 7 мулов, каждый мул тащит 7 мешков, в каждом мешке находится 7 хлебов, у каждого хлеба лежит 7 ножей, каждый нож нарежет 7 кусков хлеба. Чему равно общее число всего перечисленного?
В историческом отношении эта задача интересна тем, что она тождественна с задачей, которая встречалась в папирусе Ринда (Египет), то есть через три тысячи лет после египетских школьников задачу предлагалось разрешить итальянским школьникам.
Слайд 77
Общее число всего перечисленного
7+49+343+2401+16807+117649=137256
1
7
6
5
4
3
2
У каждой старухи 7
мулов - всего 49 мулов
Каждой мул тащит 7 мешков-
всего 343 мешка
В каждом мешке 7 хлебов - всего 2401 хлеб
У каждого хлеба лежит 7 ножей –всего 16807ножей
Каждый нож нарежет 7 кусков хлеба – всего 117649 кусков хлеба
Слайд 78
Другой способ решения задачи
7, 49, 343,
2401, 16807, 117649
–это геометрическая прогрессия, первый член b1=
7 и знаменатель прогрессии q=7.
bn= b1 q n-1. b6= 7 ·76-1= 7 ·75= 76= 117649.
Sn =(b1(q n -1))/(q-1);
S6 = (7(7 6 -1))/(7-1) = (7(117649 -1))/6=
=7 ·117648:6=137256.
Слайд 79
Шли семь старцев
У каждого старца по семь костылей;
На каждом костыле по семь сучков;
На каждом сучке
по семь кошелей;
В каждом кошеле по семь пирогов;
В каждом пироге по семь воробьёв.
Сколько всего воробьёв?
Ответ: 117649 воробьёв
Каждый из 7 человек имеет 7 кошек. Каждая кошка съедает по 7 мышек, каждая мышка за одно лето может уничтожить 7 ячменных колосков, а из зёрен одного колоска может вырасти 7 горстей ячменного зерна. Сколько горстей зерна ежегодно спасается благодаря кошкам?
Ответ: 16807 горстей
Еще две старинные задачи
Слайд 80
Искусство Леонардо в решении числовых задач изумляло всех.
Высокая репутация Фибоначчи привлекла однажды (в 1225 г.) в
Пизу государя Римской империи Фридриха II, который приехал в сопровождении группы математиков, желавших публично испытать Леонардо. Одна из задач, предложенных на турнире, имела следующее содержание:
Найти полный квадрат, остающийся полным квадратом как после увеличения его, так и после уменьшения на 5. Напомню, что полным квадратом называется число, из которого точно извлекается квадратный корень.
Фибоначчи после некоторых размышлений нашел такое число. Оно оказалось дробным: 1681/144 или (41/12)2.
Какими соображениями руководствовался Фибоначчи во время турнира, мы никогда не узнаем, но задачу он решил блестяще.
Слайд 81
В XIX веке в Пизе
был поставлен
памятник
учёному
Слайд 83
ИНФУЗОРИИ…
Летом инфузории размножаются бесполым способом делением пополам.
Вопрос: сколько
будет инфузорий после 15-го размножения?
Все организмы обладают интенсивностью
размножения
в геометрической прогрессии
Слайд 84
РЕШЕНИЕ
b15 = 2·214 = 32 768
Численность любого вида
при отсутствии ограничений растёт в соответствии с геометрической прогрессией;
Кривая роста численности любого вида при отсутствии ограничений называется экспонентой.
Слайд 85
Известно, что бактерии размножаются делением:
одна бактерия делится на две; каждая из этих двух
в свою очередь тоже делится на две, и получаются четыре бактерии; из этих четырех в результате деления получаются восемь бактерий и т. д. Результат каждого удвоения будем называть поколением.
бактерии…
Слайд 86
Способность к размножению у бактерий
настолько велика, что если бы они не гибли от
разных причин, а беспрерывно размножались, то за трое суток общая масса потомства одной только бактерии могла бы составить 7500 тонн. Таким громадным количеством бактерий можно было бы заполнить около 375 железнодорожных вагонов.
бактерии…
Слайд 87
Задача №524. [Алгебра. 9 класс, в 2ч. Ч.2.
Учебник для общеобразовательных учреждений/ Мордкович А.Г., П.В. Семенов ,
-М.: Мнемозина, 2010, -224с.(108) ]
Бактерия, попав в живой организм, к концу 20-й минуты делится на две бактерии, каждая из них к концу следующих 20 минут делится опять на две и т.д. Найдите число бактерий, образующихся из одной бактерии к концу суток.
Решение. В сутках 1440 минут, каждые двадцать минут появляется новое поколение - за сутки 72 поколения. По формуле суммы n первых членов геометрической прогрессии, у которой b1=1, q=2, n=72, находим, что S72=272-1= 4 722 366 482 869 645 213 696 - 1=
= 4 722 366 482 869 645 213 695.
Слайд 88
Всего бактерий
4 септиллиона
722 сектиллиона
366 квинтиллионов
482 квадриллионов
869 триллиона
645
миллиарда
709 миллионов
213 тысяча 695
Слайд 89
Интенсивность размножения бактерий используют…
в пищевой
промышленности
(для приготовления
напитков,
кисломолочных
продуктов,
при квашении, солении и др.)
в
сельском
хозяйстве
(для приготовления
силоса, корма
для животных и др.)
в фармацевтической промышленности (для создания лекарств, вакцин)
в коммунальном
хозяйстве и
природоохранных
мероприятиях
(для очистки сточных
вод,ликвидации
нефтяных пятен)
Слайд 90
“Потомство пары мух съест
мёртвую лошадь также скоро как лев”.
Карл Линней Девятое поколение одной
пары мух наполнило бы куб,
сторона которого равна 140 км,
или же составило бы нить,
которой можно опоясать земной
шар 40 млрд. раз.
мухи…
Слайд 91
“Потомство одного одуванчика за 10
лет может покрыть пространство в 15 раз больше
суши земного шара”.
К. А. Тимирязев
одуванчик…
Слайд 92
ЗАДАЧА
Одно растение одуванчика занимает на земле площадь 1
кв. метр и даёт в год около 100 летучих
семян.
а) Сколько кв. км площади покроет всё потомство одной особи одуванчика через 10 лет при условии, если он размножается беспрепятственно по геометрической прогрессии?
б) Хватит ли этим растениям на 11-й год места на поверхности суши земного шара?
Слайд 93
ОТВЕТ
Одно растение одуванчика занимает на земле площадь 1
кв. метр и даёт в год около 100 летучих
семян.
а) Сколько кв. км площади покроет всё потомство одной особи одуванчика через 10 лет при условии, если он размножается беспрепятственно по геометрической прогрессии?
[1012 км2]
б) Хватит ли этим растениям на 11-й год места на поверхности суши земного шара?
[нет, Sсуши = 148 млн км2]
Слайд 94
ТЛИ…
Всего за пять поколений, то
есть за 1
– 1,5 летних месяцев,
дна единственная тля может
оставить более
300 млн.
потомков, а за год её потомство
способно будет покрыть
поверхность земного шара слоем
толщиной почти в 1 метр.
Слайд 95
ВОРОБЬИ
Потомство пары птиц величиной с воробья при продолжительности
жизни в четыре года может покрыть весь земной шар
за 35 лет.
Слайд 96
Еще две биологические задачи
При каждом делении амёбы
получается две новые особи. Сколько особей будет после 6
делений? После 10 делений?
Гидра размножается почкованием, причём при каждом делении получается 5 новых особей. Какое количество делений необходимо для получения 625 особей?
Слайд 98
Положение некоторых видов на кривой
вероятности попадания в Красную книгу, построенной на основе годовой
плодовитости. Зубр, тигр и русская выхухоль находятся в Красной книге. В качестве примера вида, которого нет в Красной книге, показан кролик.
Слайд 99
Прогрессии
в банковских расчетах,
в промышленности,
в разных отраслях
науки,
в сельском хозяйстве
Слайд 100
Прогрессии и банковские расчеты
Представьте себе, что вы
открыли в банке вклад в сумме а р. Под
р% годовых на t лет. У вас есть две стратегии поведения: либо в конце каждого года хранения вклада снимать проценты по вкладу, т.е. полученную прибыль в размере р., либо прийти в банк один раз — в конце срока хранения вклада. Kaкой доход вы получите в том и другом случаях?
В первом случае при t = 1 вы получите (а + )р., при
t = 2 ваша итоговая сумма составит (а + )р., при t = 3
(а + )р. и т. д. Математическая модель ситуации — конечная
арифметическая прогрессия а, а + , а + ,а + …, а + .
Итак, при первой стратегии поведения за t лет вы получит)
а(1 + )— это так называемая формула простых процентов
Слайд 101
Прогрессии и банковские расчеты
Если вы
решили прийти в банк только в конце срока хранения
вклада, то при t = 1 получаемая сумма составит, как и в первом случае, (а + )р., т. е. а (1 + )р.; сумма вклада увеличится в (1 + )раз.
Во столько же раз она увеличится и к концу второго года хранения, и к концу третьего года хранения и т. д.
Математическая модель ситуации — конечная геометрическая прогрессия а, а(1 + ), а(1 + )2,а(1 + )3,…, а(1 + )t.
Итак, при второй стратегии поведения за t лет вы получите
а(1 + )tруб..— это так называемая формула сложных процентов.
Слайд 102
Прогрессии и банковские расчеты
Рассмотрим конкретный пример.
Пусть вклад составляв 10 000 р., банк дает
10% годовых, срок
хранения вклада - 5 лет. Если вы выбрали стратегию простых
процентов, то к концу срока хранения вы получите в итоге сумму,
равную10 000 • (1 + ) , т. е. 15 000 р. Если же вы выбрали стратегию
сложных процентов, то к концу срока хранения вы получите
в итоге сумму, равную 10 000 • ( 1 + )5, т. е. 16 105,1 р.
Как говорится в одном рекламном слогане, почувствуйте разницу.
[Алгебра. 9 класс, в 2ч. Ч.1. Учебник для
общеобразовательных учреждений/ Мордкович А.Г.,
П.В. Семенов ,-М.:Мнемозина,2010,-224с.(с.169-171) ]
Слайд 103
Директоры двух заводов
А и В встретились на совещании. Из их беседы
выяснилось, что оба завода выпустили за последний год одинаковые количества продукции, а именно по 1000 т металлических изделий. На совещании было решено добиваться дальнейшего роста продукции, причём был намечен ежегодный прирост на 40%.
Задачи на прогрессии
Слайд 104
Директор завода А выполнял задание следующим образом. В
первый год после совещания его завод выпустил на 40%
больше, чем раньше, т. е. на две пятых, а именно:
1000 +1000 • 2/5 = 1000 + 400 =1400.
За второй год завод выпустил ещё на 400 т больше,
т. е.
1400 + 400=1800,
и так далее. В результате выпуск изделий за последующие 4 года оказался таким:
до совещания.......1000,
1-й год..........1400,
2-й »........ 1800,
3-й ».......... 2200,
4-й ».......... 2600.
Слайд 105
Директор завода В поступил иначе. За первый год
после совещания он выпустил на 40% больше, чем раньше,
т. е.
1000 +1000 • 2/5 =1400 т.
За второй год директор завода В добился дальнейшего, роста производительности труда, и завод выпустил за второй год на 40% больше, чем за первый год:
1400 + 1400 • 2/5 = 1400 + 560 = 1960 т.
На третий год он составил план по тому же принципу: опять увеличить выработку на 40% по сравнению с предыдущим годом:
1960+ 1960 • 2/5 = 1960 + 784 = 2744 т.
За четвёртый год завод В дал такую выработку:
2744 + 2744 • 2/5 = 2744 + 1098 = 3842.
В результате выпуск изделий заводом В оказался следующим:
до совещания.......1000,
1-й год..........1400,
2-й »........ 1960,
3-й ».......... 2744,
4-й ».......... 3842.
Заметим, что коэффициент увеличения здесь равен 7/5
, так как выпуск каждого года составляет 140% предыдущего года,
140%= 140/100 = 7/5 .
Через 4 года директоры заводов А и В снова встретились на совещании и сравнили выработку обоих заводов. Оказалось, что завод В выпустил значительно больше изделий, чем завод A.
Завод А сохранял всё время одну и ту же надбавку, равную 400 т в год. Завод В сохранял неизменным отношение выработки двух соседних лет, т. е. коэффициент увеличения k = 7/5 .
Слайд 107
Представим на графике продукцию
того и другого завода
Слайд 108
Как сосчитать количество бревен?
Представьте, что вы – учетчик
на стройке. Привезли большое количество бревен строевого леса. Нужно
быстро определить, сколько бревен привезли, чтобы закрыть наряд шоферу.
В данном случае, чтобы подсчет бревен осуществлялся по простым формулам, один из способов – использовать естественное расположение бревен так, чтобы в каждом верхнем ряду их оказалось на единицу меньше, чем в нижнем. Тогда число бревен ряда образует арифметическую прогрессию и общее количество легко подчитывается по формуле суммы арифметической прогрессии с разностью, равной единице.
Слайд 109
Еще две технические задачи
После каждого движения поршня разрежающего
насоса из сосуда удаляется 20% находящегося в нём воздуха.
Определите давление воздуха внутри сосуда, после 6 движений поршня, если первоначально давление было 760 мм.рт.ст.
Тело в первую секунду движения прошло 7 м, а за каждую следующую секунду – на 3 м больше, чем за предыдущую. Какое расстояние тело прошло за восьмую секунду?
Слайд 110
В каких процессах ещё встречаются
такие закономерности?
Деление ядер
урана происходит с помощью нейронов. Нейтрон, ударяя по ядру
урана раскалывает его на две части. Получается два нейтрона. Затем два нейтрона, ударяя по двум ядрам, раскалывают их еще на 4 части и т.д. — это геометрическая прогрессия.
При повышении температуры в арифметической прогрессии скорость химической реакции вырастает в геометрической прогрессии.
Возведение многоэтажного здания — пример арифметической прогрессии. Каждый раз высота здания увеличивается на 3 метра.
Слайд 111
Вписанные друг в друга правильные треугольники — это геометрическая
прогрессия.
Денежные вклады под проценты — это пример геометрической последовательности.
Зная формулы суммы членов геометрической последовательности, можно подсчитывать сумму на вкладе.
Равноускоренное движение — арифметическая прогрессия, т.к. за каждые промежутки времени тело увеличивает скорость в одинаковое число раз.
Слайд 112
Задачи на применение прогрессий встречаются
в старых
учебниках
по математике
Слайд 113
Купец имел 14 чарок серебряных, причем веса чарок
растут по арифметической прогрессии с разностью 4. Последняя чарка
весит 59 латов. Определить, сколько весят все чарки.
Решение
а14=а1+13d, a1=59-13·4=7,
S14=(7+59)/2·14=462.
Ответ: все чарки весят 462 лата.
Задачи из «Арифметики» Л.Ф.Магницкого
Садовник продал первому покупателю половину всех яблок и
ещё пол-яблока, второму покупателю – половину оставшихся и ещё пол-яблока; третьему – половину оставшихся и ещё пол-яблока и так далее. Седьмому покупателю он продал половину оставшихся яблоки ещё пол-яблока; после этого яблок у него не осталось. Сколько яблок было у садовника?
Задачи из «Арифметики» Л.Ф.Магницкого
Слайд 115
Решение. Пусть у садовника было х яблок.
Слайд 116
Составим уравнение:
- геометрическая прогрессия, где
, n = 7, .
Уравнение примет следующий вид:
x=127
Ответ: 127 яблок было у садовника.
Слайд 117
В «Сборнике алгебраических задач» (часть
вторая, авторы Шапочников Н.А., Вальцов Н.К.; Москва, Ленинград, Учпедгиз,
1949) было найдено двадцать задач на арифметическую прогрессию.
Слайд 118
Работники нанялись вырыть колодезь с таким
условием, чтобы за первый аршин глубины им заплатили 40
копеек, а за каждый следующий 15-ю копейками больше, чем за предыдущий. Сколько аршин вырыли они, если за всю работу получили 16 р. 90 к.?
Решение. a1=40, d=15, Sn=1690. Найти n.
Sn=(2a1+d(n-1))∙n:2; n>0;
1690=(80+15(n-1))∙n:2;
1690=(80+15(n-1))∙n:2;
3380=(65+15n)∙n;
15n2+65n-3380=0;
3n2+13n-676=0;
n1=-52/3; n2=13.
Так как по условию задачи n>0, то n=13.
Работники выкопали колодец глубиной 13 аршин.
Слайд 119
Некто, будучи должен 720 руб., обязался уплачивать
этот долг по частям, выдавая каждый месяц 10-ю рублями
меньше, чем в предыдущий. Сколько он уплатил в первый месяц и во сколько времени погасил весь свой долг, если в последний месяц ему пришлось отдать 40 р.?
Решение. Применим формулы п –го члена и суммы п первых членов арифметической прогрессии получим систему уравнений:
a1-10n-30=0,
a1n+10n-1440=0;
Решив эту систему способом подстановки, найдем n=-16 и n=9. Так как n>0, то приходим к выводу, что свой долг человек вернул за 9 месяцев, отдав в первый месяц 120 рублей.
Слайд 120
Два тела движутся навстречу одно другому из
двух мест, находящихся в расстоянии 153 футов. Первое проходит
по 10 футов в секунду, а второе в первую секунду прошло 3 фута и в каждую следующую секунду проходит 5-ю футами больше, чем в предыдущую, Через сколько секунд тела встретятся?
Решение. Второе тело пройдет за n сек
Sn=(2a1+d(n-1))∙n:2=(2·3+5 ·(n-1))∙n:2= =(1+5n)∙n:2 (фут), а первое тело - 10n фут,
((1+5n)∙n:2+ 10n) фут – расстояние между телами в начальный момент, по условию оно равно 153 футам. (1+5n)∙n:2+ 10n=153. n=6, n=-10,2. Так как n>0, то n=6.
Значит, тела встретятся через 6 секунд.
Слайд 121
Числа градусов, содержащихся в
последовательных внутренних углах некоторого многоугольника, составляют прогрессию, разность
которой 10; наименьший угол этого многоугольника 100°. Сколько в многоугольнике сторон?
Решение. Sn=(2a1+d(n-1))∙n:2= =(200+10(n-1))∙n:2=5n2+85n. Сумма внутренних углов многоугольника находится по формуле, известной из геометрии: (n-2)·180.
5n2+95n= 180n-360;
5n2-85n+360=0;
n2-17n+72=0;
n=8, n=9.
Существует два многоугольника, удовлетворяющие условию задачи.
Слайд 122
Известно, что свободно падающее тело проходит в первую
секунду 16,1 фута, а в каждую следующую на 32,2
фута больше, чем в предшествующую. Если два тела начали падать с одной высоты, спустя 5 секунд одно после другого, то через сколько секунд они будут друг от друга на расстоянии 724,5 фута?
Решение. Найдем путь каждого тела.
St+5-St=724,5; 16,1(t+5)2-16,1t2=724,5;
t=2.
Тела будут друг от друга на расстоянии
724,5 фута через 2 секунды.
Слайд 123
Задачи на применение прогрессий встречаются
в книгах
по занимательной математике
Слайд 124
Царь древней Индии
Шерам пригласил к себе изобретателя шахмат Сета и спросил,
какую бы
награду хотел бы он получить за изобретение столь
мудрой игры.
Тогда Сета попросил царя на первую клетку
шахматной доски положить 1 зерно, на вторую – 2 зерна,
на третью – 4, на четвертую – 8 и т.д., т.е. на каждую
клетку вдвое больше зерна, чем на предыдущую клетку.
Поначалу царь удивился столь “скромному” запросу
изобретателя и поспешно повелел выполнить ту просьбу.
Однако, как выяснилось, казна царя оказалось слишком
“ничтожной” для выполнения этой просьбы.
Древняя индийская легенда
Слайд 125
Действительно, чтобы выполнить эту
просьбу, потребовалось бы количество зерен, равное сумме 1 +
2 + 22 +.. + 263, а эта сумма равна 18446744073709551615.
Если считать, что 1 пуд зерна содержит 40000 зерен, то для выполнения просьбы потребовалось бы 230 584 300 921 369 пудов зерна. Если полагать, что в среднем ежегодно собирается 1 000 000 000 пудов зерна, то для выполнения указанной просьбы нашей стране нужно работать (не расходуя ни одного зерна) на протяжении 230584 лет.
Слайд 126
Столько зёрен
должен был получить
изобретатель шахмат:
S64=264-1=
=18446744073704551615
Слайд 127
Всего зерен
18 квинтиллионов
446 квадриллионов
744 триллиона
73 миллиарда (биллиона)
709
миллионов
551 тысяча 615
1 = 1,84 · 1019
- стандартный вид
данного числа
Слайд 129
Однажды богач заключил выгодную, как
ему казалось, сделку с человеком, который целый месяц ежедневно
должен был приносить по 100 тыс. руб., а взамен в первый день месяца богач должен был отдать 1 коп., во второй-2 коп., в третий-4 коп., в четвертый-8 коп. и т. д. в течении 30 дней. Сколько денег получил богач и сколько отдал? Кто выиграл от этой сделки?
Это задача из «Сборника старинных занимательных задач по математике» Игнатьева Е.И.
Слайд 130
Считают “мужик” и “купец”
“Мужик” заплатил: S30 =
100 000• 30 = 3 000 000 (рублей).
“Купец” заплатил: 1; 2; 4;…
q=2/1=2.
S30 =1• (230 – 1):(2-1)= 2 30 -1= =1 073 741 824 -1 =1 073 741 823 (коп.) т.е. 10 738 418 руб.23коп
Слайд 131
О поселковых слухах:
Удивительно, как
быстро разбегаются по посёлку слухи! Иной раз не пройдет
и двух часов со времени какого– нибудь происшествия, которое видели всего несколько человек, а новость уже облетела весь посёлок: все о ней знают, все слышали. Итак, задача:
В поселке 16 000 жителей. Приезжий в 8.00 рассказывает новость трем соседям; каждый из них рассказывает новость уже трем своим соседям и т. д. Во сколько эта новость станет известна половине посёлка?
Слайд 132
Решение. Итак, в 8. 15 утра новость была
известна только четверым: приезжему и трём местным жителям. Узнав
эту новость, каждый из трёх граждан поспешил рассказать её трём другим. Это потребовало также четверти часа. Значит, спустя полчаса после прибытия новости в город о ней узнали уже 4+3·3=13 человек. Каждый из девяти вновь узнавших поделился в ближайшие четверть часа с тремя другими гражданами, так что к 8.45 утра новость стала известна 13+9·3= 40 гражданам. Если слух распространяется по посёлку и далее таким способом, то есть каждый узнавший эту новость успевает в ближайшие четверть часа передать её трём согражданам, то осведомление посёлка будет происходить по следующему расписанию:
в 9.00 новость узнают 40+27 ·3=121 (человек);
9.15 121+81 ·3 =364 (человек);
9.30 364+243 ·3=1093 (человек);
9.45 1093+729 ·3=3280 (человек);
10.00 3280 + 2187 ·3 =9841(человек).
Слайд 133
Эту задачу можно решить по-другому, используя формулу сумму
n первых членов геометрической прогрессии.
В данном случае: q
= 3, b1 = 1, Sn = 8000, n –неизвестно.
Подставляя известные числа в формулу, получим:
Чтобы найти n , заметим, что 36 = 729, 32 =9,
38 = 36· 32= 729 · 9=6561, 39=19683.
Значит, n должно быть не меньше 9. При n = 9 имеем:
Значит, на 9-ом шаге более половины жителей города будут знать новость. Легко подсчитать, что это произойдёт в 10.00 утра.
Слайд 134
Задачи на прогрессии есть
и в книгах Я.И.
Перельмана
Прогрессии в литературе:
строки из “Евгения Онегина”.
«…Не мог он ямба от хорея
Как мы не бились отличить…». Отличие ямба от хорея состоит в различных расположениях ударных слогов стиха.
Ямб – это стихотворный размер с ударением на четных слогах 2; 4; 6; 8;…Номера ударных слогов образуют арифметическую прогрессию с первым членом 2 и разностью прогрессии 2.
Хорей – это стихотворный размер с ударением на нечетные слогах стиха. Номера ударных слогов образуют арифметическую прогрессию 1; 3; 5; 7;..
Примеры.
Ямб. «Мой дЯдя сАмых чЕстных прАвил…», прогрессия 2; 4; 6; 8;…
Хорей. «Я пропАл, как звЕрь в загОне»Б.Л.Пастернак, «БУря мглОю нЕбо крОет» А.С. Пушкин, прогрессия 1; 3; 5;7.
Слайд 136
О финансовых пирамидах:
Разберёмся в механизмах этих организаций. Организатор
начинает вовлекать в свою организацию и говорит, что, если
внести указанную плату по указанным адресам по 1 рублю, а затем заплатить ещё по 5 таким же адресам, вычеркнув первый адрес и дописав свой последним, то через некоторое время вы получите уйму денег. Хотя желающих разбогатеть по щучьему веленью немало, но в выигрыше оказываются только учредители такой игры.
Решение. Дело в том, что число участников увеличивается в 5 раз с каждым кругом. Если пятёрка устроителей подпишет, допустим, 120 человек со своими адресами, то в первом круге участвуют 120 человек, во втором – 600, в третьем – 3 000, …, в десятом – 234 375 000 человек; это намного больше населения страны. Так что участник, включившийся в восьмом или девятом круге, уже ничего не получит.
Слайд 137
Выводы.
Установили, что сами по себе прогрессии известны так

давно, что нельзя говорить о том, кто их открыл.
Убедились
в том, что задачи на прогрессии, дошедшие до нас из древности, также как и многие другие знания по математике, были связаны с запросами хозяйственной жизни: распределение продуктов, деление наследства и другими.
Выяснили, что в развитие теории о прогрессиях внесли ученые Архимед, Пифагор и его ученики, французские математики Леонард Фибоначчи и Баше де Мезириака, немецкие математики М. Штифель, Н. Шюке, и К. Гаусс.
Нашли много задач на арифметическую и геометрическую прогрессию в старых и в современных учебниках по математике. Заметили, что арифметическая прогрессия в практических задачах встречается чаще геометрической. Много задач с практическим содержанием в учебнике для 9 класса под редакцией Г.В. Дорофеева [4].
Обнаружили, что интенсивное размножение бактерий в геометрической прогрессии широко применяется в пищевой промышленности, в фармакологии, в медицине, в сельском и коммунальном хозяйствах, в банковских расчетах (начисление сложных процентов).